2020牛客暑期多校训练营（第四场) B.Basic Gcd Problem（数学）

题目传送
题意:
给定一个函数

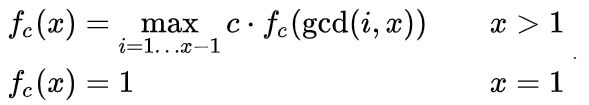
给你x和c，问这个函数的值是多少?

思路:
首先得把这个函数看懂，要是看都没看懂，还怎么做题。
举个例子:f(8)的最大值为 f(8) = c * f(gcd(8,4) == 4)，那么f(4) = c * f(gcd(4,2) == 2) ， f(2) = c * f(gcd(2,1) == 1) = c
综上:max f(8) = c * c * c

可以注意到，这个函数的递归退出条件就是gcd(i,x) == 1的时候，这时的f(1) = 1，那么既然退出递归的时候f(x)的值是定值1，那么最大值的影响关键就是递归的长度了换句话来说，递归得越久，那么乘c的次数就越多 ，那么我们如何让他递归得越久呢?

因为f(x)的值是与gcd相关的，·所以我们分解x的质因子数量就可以了。为什么这样做呢?既然要递归得越长，那么我们就要充分的去利用他质因子，把每一个质因子利用起来，就可以得到最长的递归次数。

这里也举个例子叭，
8 = 2 * 2 * 2，那么就可以递归3次，第一次 8 = 4 * 2，所以gcd(8,4)，这样就利用了一个质因子2，依次类推

但是这个题比较卡时间，还得在预处理一下所有的数的质因子个数，不然还是会t掉。那么接下来将要讲讲代码的优化了

如果不带快速幂，普通的打表也过不了，还得在打表上优化。

普通打表

	int arr[N] = {0};//N == 1e6 + 5
    for(int i = 1;i <= N;i++)
    {
        int sum = 0,n = i;
        for(int j = 2;j * j <= n;j++)
            while(n % j == 0)
                sum++,n/=j;
        if(n > 1) sum++;//标准的质因数分解模板，分解出来个数
        arr[i] = sum;
    }

优化打表

	int arr[N] = {0};//N == 1e6 + 5
    for(int i = 1;i <= N;i++)
    {
        int sum = 0,n = i;
        for(int j = 2;j * j <= n;j++)
        {
            while(n % j == 0)
            {
                sum++,n/=j;
                if(arr[n] != 0)//这个数前面已经处理过了，那么就直接加就可以了，不用再判断了
                {
                    arr[i] = arr[n] + sum;
                    n = 0;
                    break;
                }
            }
            if(n == 0) break;
        }
        if(n == 0) continue;
        if(n > 1) sum++;
        arr[i] = sum;
    }

快速幂优化

ll quick_pow(ll a,ll b,ll mod)
{
    ll ans = 1;
    while(b)
    {
        if(b&1)
            ans = a*ans%mod;
        b>>=1;
        a = a*a%mod;
    }
    return ans%mod;
}

AC代码

#include 
using namespace std;
const int N = 1e6 + 5;
const int mod = 1e9+7;
typedef long long ll;
int arr[N],t;
ll quick_pow(ll a,ll b)
{
    ll ans = 1;
    while(b)
    {
        if(b&1)
            ans = a*ans%mod;
        b>>=1;
        a = a*a%mod;
    }
    return ans%mod;
}
signed main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    for(int i = 1;i <= N;i++)
    {
        int sum = 0,n = i;
        for(int j = 2;j * j <= n;j++)
        {
            while(n % j == 0)
            {
                sum++,n/=j;
                if(arr[n] != 0)
                {
                    arr[i] = arr[n] + sum;n = 0;
                    break;
                }
            }
            if(n == 0) break;
        }
        if(n == 0) continue;
        if(n > 1) sum++;
        arr[i] = sum;
    }
    scanf("%d",&t);
    while(t--)
    {
        ll n,c;
        scanf("%lld %lld",&n,&c);
        printf("%lld\n",quick_pow(c,arr[n]));
    }
}