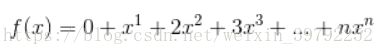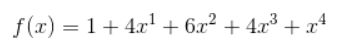数论继续学习16---母函数（又名生成函数）

数论继续学习16---母函数（又名生成函数）

 

前言：

母函数是个很难的东西，难在数学

而ACM中所用的母函数只是母函数的基础

应该说除了不好理解外，其他都是非常简单的

 

母函数即生成函数，是组合数学中尤其是计数方面的一个重要理论和工具。

但是ACM中的母函数木有像数学那么深究，应用的都是母函数的一些基本

（就好比方程的配方，因式的分解，写起来容易，你用电脑写起来就麻烦了，所以学计算机就不要老跟数学家瞎闹(￣３￣)）

 

什么是母函数

就是把一个已知的序列和x的多项式合并起来，新产生的多项式就叫原来序列的母函数

至于怎么合并，看这个例子

 

序列{0，1，2，3，4，5，...，n}的母函数就是

（这个x没有任何意义，应该说，我们不需要把它当做一个函数，我们只要知道母函数这么写就可以了）

 

序列{1,1,1,1,1......}的母函数就是

 

二项式展开的序列比如这个{1,4,6,4,1,0,0,0,0,0.....}是C(4,0)到C(4,4)的系数，那它的母函数就是

母函数就长这样，对正常人来讲，这种东西毫无意义( ° △ °|||)

我们可能不是正常的人？ 那看点有意义的东西：

 

例题1：有1克、2克、3克、4克的砝码各一枚，能称出哪几种重量？每种重量各有几种可能方案？

假如x的幂次数表示几克的砝码，那么

1克的砝码表示为1+x^1

2克的砝码表示为1+x^2

3克的砝码表示为1+x^3

4克的砝码表示为1+x^4

 

每个砝码都可以选择取或不取

所以这里的1可以认为1*x^0，表示不取这颗砝码

 

那么把这些乘起来

 

根据指数来看，我们可以称出0~10这么多的重量，其中3~7的系数为2，说明有2种称的方法

分毫不差(・ˍ・*)

所以说母函数在ACM就是这么用的，跟函数没关系，跟写法有关系。。。

 

例题2：求用1分、2分、3分的邮票贴出不同数值的方案数：（每张邮票的数量是无限的）

那么

1分：(1+x^1+x^2+x^3+x^4+......)

2分：(1+x^2+x^4+x^6+x^8+......)

3分：(1+x^3+x^6+x^9+x^12+......)

然后这3个乘起来（让电脑去乘吧）

 

对于这种无限的，题目肯定会给你他询问的数值的范围，计算到最大的范围就可以了

 

 

附代码：

#include
typedef long long LL;
const int N = 100 + 5;//假如题目只问到100为止 
const int MAX = 3;//题目只有1,2,3这3种邮票 
LL c1[N], c2[N];//c2是临时合并的多项式，c1是最终合并的多项式 
int n;
void init(){
    c1[0] = 1;//一开始0的情况算一种 
    for(int i = 1; i <= MAX; i ++){//把1分到MAXN的邮票合并，变成一个多项式 
        for(int j = 0; j < N; j += i){//i分的邮票，步长是i
            for(int k = 0; j + k < N; k ++){//从x^0到x^N遍历一遍 
                c2[j + k] += c1[k];//因为j的所有项系数为1，所以c1[k]可以看成c1[k]*1; 
            }
        } 
        for(int j = 0; j < N; j ++){//把c2的数据抄到c1，清空c2 
            c1[j] = c2[j];
            c2[j] = 0;
        }
    }
} 
int main(){
    init();
    while(scanf("%d", &n) != EOF){
        printf("%I64d\n", c1[n]);
    }
}

我们就来把这个模板用于实际吧

 

hdu 1028 Ignatius and the Princess III

题目问一个数字n能够拆成多少种数字的和

比如n=4

  4 = 4;
  4 = 3 + 1;
  4 = 2 + 2;
  4 = 2 + 1 + 1;
  4 = 1 + 1 + 1 + 1;

有5种，那么答案就是5

AC代码（预处理我不是这样写的）：

#include
typedef long long LL;
const int N = 120 + 5;
const int MAX = 120 + 5;
LL c1[N], c2[N];
int n;
void init(){
    c1[0] = 1;
    for(int i = 1; i <= MAX; i ++){
        for(int j = 0; j < N; j += i){
            for(int k = 0; j + k < N; k ++){
                c2[j + k] += c1[k];
            }
        } 
        for(int j = 0; j < N; j ++){
            c1[j] = c2[j];
            c2[j] = 0;
        }
    }
} 
int main(){
    init();
    while(scanf("%d", &n) != EOF){
        printf("%I64d\n", c1[n]);
    }
}

hdu 1398 Square Coins

题目说一个国家的硬币都是方形的，面值也是方形的

有1块钱，4块钱，9块钱，16块钱......一直到289块钱（17^2）

问想组成n块钱有几种方法

#include
#define ll long long
using namespace std;

ll cnt1[308], cnt2[308];
int n;

void init()
{
    cnt1[0] = 1;
    for(int i = 1; i <= 17; i++)
    {
        memset(cnt2, 0, sizeof(cnt2));
        for(int j = 0; j < 307; j += i*i)
            for(int k = 0; j + k < 307; k++)
                cnt2[j+k] += cnt1[k];
        for(int j = 0; j < 307; j++) cnt1[j] = cnt2[j];
    }
}



int main()
{
    init();
    while(~scanf("%d", &n))
    {
        if(n == 0) break;
        printf("%lld\n", cnt1[n]);
    }
    return 0;
}

都是改一些小地方，都是模板题(oﾟωﾟo)

 

 

最后一道

hdu 1085 Holding Bin-Laden Captive!

AC代码：

#include
#include
typedef long long LL;
const int N = 1000 * (1+2+5) + 5;
int cost[3] = {1, 2, 5};
LL c1[N], c2[N];
int num[3];
int MAX;
int main(){
    while(~scanf("%d%d%d", &num[0], &num[1], &num[2])){
        if(num[0] == 0 && num[1] == 0 && num[2] == 0) break;
        memset(c1, 0, sizeof(c1));
        memset(c2, 0, sizeof(c2));
        MAX = num[0] + num[1] * 2 + num[2] * 5;//计算最大值
        c1[0] = 1;
        for(int i = 0; i < 3; i ++){
            for(int j = 0; j <= num[i] * cost[i]; j += cost[i]){
                for(int k = 0; j + k <= MAX; k ++){
                    c2[j + k] += c1[k];
                }
            } 
            for(int j = 0; j < N; j ++){
                c1[j] = c2[j];
                c2[j] = 0;
            }
        }
        for(int i = 1; i <= MAX + 1; i ++){
            if(!c1[i]){
                printf("%d\n", i);
                break;
            }
        }
    }
}

母函数在数学上真的用处很大。

但上面的3个例题，都有更快的做法

 

第一题：动态规划，时间复杂度O(n^2)

#include
const int N = 120 + 5;
int dp[N];
int n;
void init(){
    dp[0] = 1;
    for(int i = 1; i < N; i ++){
        for(int j = i; j < N; j ++){
            dp[j] += dp[j - i];
        }
    }
}
int main(){
    init();
    while(scanf("%d", &n) != EOF){
        printf("%d\n", dp[n]);
    }
}

 

第二题：动态规划，时间复杂度O(n^2)

 

#include
const int N = 300 + 5;
int dp[N];
int n;
void init(){
    dp[0] = 1;
    for(int i = 1; i <= 17; i ++){
        for(int j = i*i; j < N; j ++){
            dp[j] += dp[j - i*i];
        }
    }
}
int main(){
    init();
    while(scanf("%d", &n) != EOF && n){
        printf("%d\n", dp[n]);
    }
}

第三题：≖‿≖✧特判就好了，时间复杂度O(1)

#include
int a, b, c;
int ans;
int main(){
    while(~scanf("%d%d%d", &a, &b, &c) && (a || b || c)){
        if(a >= 4 || a >= 2 && b >= 1 || a >= 1 && b >= 2) ans = a + 2*b + 5*c + 1;
        else if(a == 0) ans = 1;
        else ans = a + 2*b + 1;
        printf("%d\n", ans);
    }
}

 

经过上面的步骤，母函数我们只要暂时理解原理就好了