【论文阅读】Frame-Recurrent Video Super-Resolution (FRVSR2018超分)

【论文阅读】Frame-Recurrent Video Super-Resolution (FRVSR)

今天要整理一篇最近阅读的文章，这篇文章是2018年Mehdi S.M. Sajjadi发表在CVPR的一篇有关视频超分辨率的文章。目前作者并没有公开源码，但是我在GitHub上看到有其他大牛复现了论文源码，我暂时还没跑这篇文章的代码，不过后面会整理我所跑过的论文代码。

Abstract

摘要中，作者首先说明了目前比较前沿的视频超分辨率方法是使用CNN和运动补偿结合的。一些优秀的方法都是采用处理一个batch的LR来生成一个HR，这样做的缺点有两个：1）每个低分辨率帧会被处理多次，增加了计算量；2）每个输出帧仅根据输入帧独立估计，限制了系统生成时间连贯性的结果的能力。故，作者提出了一个端到端训练的视频超分辨率帧循环网络框架（FRVSR） ，它是使用前面生成的HR结果来估计下一帧的输出，这有助于促进输出结果的时间连贯性，同时也减少了计算量。

Introduction

主要讲述了超分辨率问题及其应用，归类了几种方法，此处略过…(太懒了，不想全部翻译一遍）下面直接说重点！！！在本文提出的FRVSR网络，有以下两点好处：1）每个输入帧只被处理一次；2）前一帧的信息通过生成的HR估计来促进下一帧的输出。
文章的贡献：

• 提出了一个循环框架，使用前一帧估计的HR生成下一帧的输出，有利于促进时间上一致；
• 提出的框架可以在更大的时间范围内传播信息，并不增加计算；
• 文章进行了大量的实验，分析了不同网络设计的性能。

FRVSR Framework

FRVSR网络结构如下图，一共有五部分构成：光流估计FNet、上采样光流Upscaling、warp前帧、映射到低维空间Map和超分辨率重建SR。

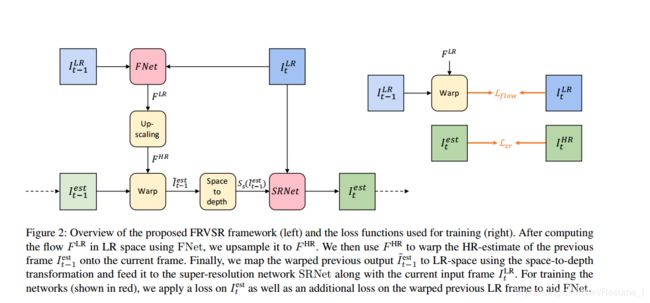
1.FNet光流估计网络

整个网络的第一步是光流估计，主要是估计低分辨率输入$I_{t-1}^{LR}$和$I_t^{LR}$之间的光流特征图，输出经过正则化处理的，第一部分用公式表达如下：
$$F^{LR}=FNet(I_{t-1}^{LR},I_t^{LR})\in [-1,1{]}^{H\times W\times 2}$$
FNet网络，输入的是$I_{t-1}^{LR}$和$I_t^{LR}$concate之后的6通道图像（假设图像是三通道的情况下），然后经过6个组件，通道数从32增加到256，再减回64，最后还有三层，卷积数为32的层，leaky relu激活层和卷积数为2的层，最终得到输入图像的光流$F^{LR}$，这里的每一层卷积核大小都是$3\times 3$，步长为1，leaky ReLU的参数为0.2。具体结构如下图，（顶部是SRNet，底部是FNet）：

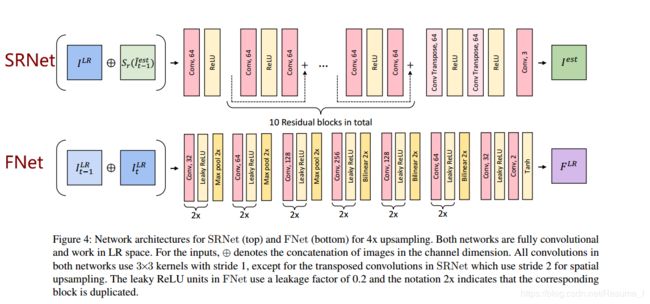
2.Upscaling flow上采样光流：

第二部分是将上一部分在低维空间得到的光流使用双线性插值上采样到高维空间中，其公式表达如下：
$$F^{HR}=UP(F^{LR})\in [-1,1{]}^{sH\times sW\times 2}$$

从直接上采样光流开始，接着后面处理的方法都跟其他论文的方法有较大的不同。这个上采样工作，博主认为带有些粗糙，但具体实现效果如何还有待探究。

3.Warping previous output：

第三部分是将上采样得到的光流，根据前一帧的结果warp，得到当前对齐的帧。一般大众的方法都是将当前的输入$I_t^{LR}$和光流$F^{LR}$进行warp的，这也是这篇文章创新的点之一，改进了以前的多帧输入，输入帧被重复处理多次的不足。该部分用公式表示如下：
$$I_{t-1}^{\prime est}=WP(I_{t-1}^{est},F^{HR})$$

4.Mapping to LR space 映射到低维空间：

第四部分的工作是将warp后得到高维空间的输出估计再映射回低维空间，这步的意义是尽量将大计算量的工作都丢在LR空间上完成，而HR空间尽量减少计算。该步使用的方法是tensorflow的space_to_depth，这个方法跟亚像素卷积层有点类似，亚像素卷积层是将$H\times W\times s^{2}c$变成$sH\times sW\times c$，是属于上采样操作，而这个space_to_depth是与其相反，可以认为是下采样操作，将$sH\times sW\times c$变成$H\times W\times s^{2}c$，具体公式表达如下：
$$S_s:[0,1{]}^{sH\times sW\times c}\to [0,1{]}^{H\times W\times s^{2}c}$$
这个操作是从图像中提取已移动的低分辨率网格并将其放入通道尺寸（这句话是直译的， 有点难翻译，所以特意把原文附上：“which extracts shifted low resolution grids from the image and places them into the channel dimension”），如果上面的描述不太懂，那上图应该比较好理解。

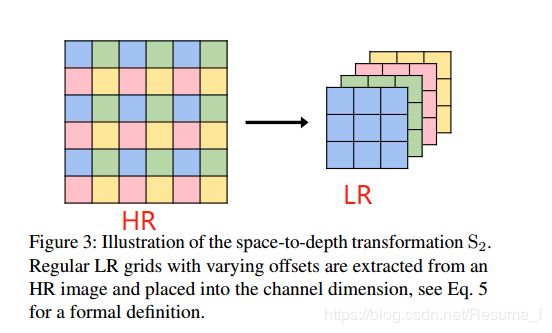
5.Super Resolution超分辨率重建：

第五部分是超分辨率重建了！！！这也是最后一部分，先将前面得到的内容（主要是两部分内容：经过mapping的$I_{t-1}^{\prime est}$和当前输入帧$I^{LR}$）都连接起来，然后馈送进SRNet网络，该网络结构图在上面第2部分的图，然后得到最终的输出。所有的部分整合成一条公式表达，如下：
$$SRNet(I_t^{LR}⨁S_s(WP(I_{t-1}^{est},UP(FNet(I_{t-1}^{LR},I_t^{LR})))))$$

到这里，FRVSR的网络结构就介绍完毕，然后接下来就到了损失函数部分了。

Loss Function

整个网络的损失函数其实由两部分组成，分别是$L_{flow}$ 和 $L_{sr}$，它们分别应用在两个主要网络中FNet和SRNet。可以看FRVSR Framework部分的右图。左图是网络结构，右图是损失函数部分。$L_{sr}$应用在SRNet，公式表达如下：
$$L_{sr}=||I_t^{est}-I_t^{HR}|{|}_2^2$$
而$L_{flow}$ 应用在FNet中，因为没有实际的光流数据集，所以增加了一个辅助的loss来帮助FNet生成更真实的光流，公式如下：
$$L_{flow}=||WP(I_{t-1}^{est},F^{HR})-I_t^{LR}|{|}_2^2$$
故，整个网络总的损失为$L=L_{sr}+L_{flow}$

实验参数说明

文章使用的数据集来自于vimeo.com的，由40个高分辨率视频(720p, 1080p和4k)组成。将视频下采样2倍，裁剪成256*256大小的视频作为HR；再对HR使用高斯模糊，下采样4倍得到的LR。输入是10个连续的帧，这些连续的帧没有场景突变的情况，也不包含关键帧 （为什么不包含关键帧？这个操作是我看过的视频超分辨率都会采用的手段，我还不知道这是为什么，如果你知道，记得评论告诉我！谢谢啦） ，初始化是第一帧是一张黑色的图。学习率固定是$10^{-4}$，batch size为4。具体参数等我尝试跑一遍再来补充。。今天的整理先到这里啦！

总结

看完整篇文章，最大的收获来源于Warping previous output 部分，这确实能达到作者所说的保持输出帧在时间上达到一致的效果，还有作者把所有需要计算的工作都转移到了低维空间上进行，这大大地减少了计算量。针对这文章，我提出个人一点点小小的见解或者说疑惑点，本篇文章主要改进点在Warping previous output 这里，作者遵循着每一帧只使用一次的原则，前面的光流估计部分以及上采样光流，都稍稍有些粗糙，因为它们都是在低维空间上进行的，那么提取到的特征并没有那么地准确，还是有些不足。涉及这个领域并不深，所以见解也不深，还是要多阅读文章！！！快过年啦，在这里也提前祝大家新年快乐，心想事成~~
如果文章对你有帮助，那你点个赞，鼓励一下我这个程序媛！附上文章的地址：
https://arxiv.org/abs/1801.04590v3

本文是原创作品，转载需要注明出处！