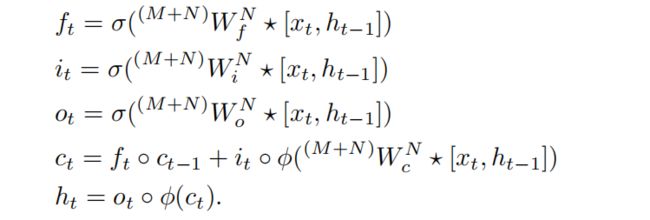视频目标检测
卷积神经网络在目标检测中发挥出重要作用[1,2,3,4,5]。
近期,新的网络结构[6,7]使得目标检测算法可以运行在计算力更低的硬件平台,并且性能足够媲美先进单幅图像目标检测算法。
然后,视频给目标检测带来了额外的时空线索,如何利用这一线索设计更好的视频目标检测框架称为目前的主要挑战。
那么可以利用的时空线索有哪些:
- 由于视频的时间连续性,相邻帧中的目标在位置上具有相似性,且不会发生实质性变化。
- 多帧之间可以反映目标的不同姿态,有利于准确定位目标。
- 时间线能够提升目标检测的置信度,增加检测稳定性[8]。
Bottleneck-LSTM 一种快速LSTM
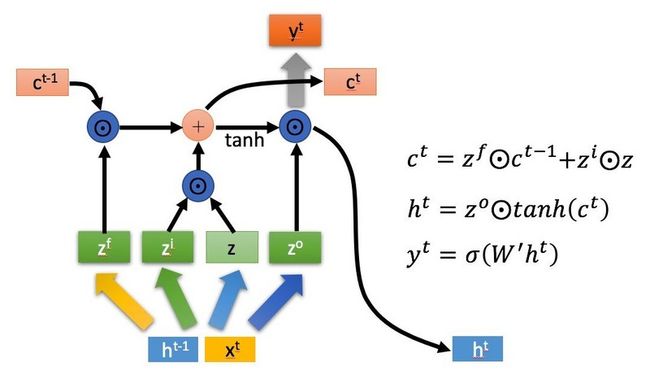
长短期记忆网络(LSTM)[9]是一种广泛使用的时序数据处理网络,结构如下图所示,其中$\odot$是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的,$\oplus$代表矩阵加法。
Convolutional LSTM是LSTM的一个特殊变种,使用3D隐层状态,并将门(Gate)计算替换为卷积层(Convolutional Layer),如此使得LSTM能够同时编码时空信息。
直接将Convolutional LSTM嵌入到目标检测网络会大幅增加计算量 ,解决这一问题的方式就是使用Bottleneck-LSTM,Bottleneck-LSTM使用深度可分离卷积(Depthwise Separable Convolutions)以及特殊设计的Bottleneck门。
我们将图像考虑为连续图像帧的序列$V=\{I_0,I_1,...,I_n\}$。
视频检测的目的是得到每一帧的检测结果$\{D_0,D_1,...,D_n\}$,其中$D_k$是$I_k$帧中一系列的预测目标外包矩形框和预测类别。
在线视频目标检测认为$D_k$仅能从$I_k$帧与之前的图像帧中进行计算。
预测模型可以看作这样一个函数$F(I_t,s_{t-1})=(D_t,s_t)$,其中$s_k=\{s_k^0,s_k^1,...,s_k^{m-1}\}$是描述$k$帧与之前的特征图向量。
$m$层LSTM的神经网络用来逼近这一函数,$s_{t-1}$的每个特征图作为LSTM的状态输入,LSTM的输出状态为$s_t$的特征图。
LSTM对特征的细化
令单幅图像目标检测器为函数$D_t=G(I_t)$。在LSTM视频检测器中,$m$个LSTM将$G$划分为$m+1$个子网络${g_0,g_1,...,g_m}$,并满足:
$G(I_t)=(g_m \circ \cdots \circ g_1 \circ g_0)(I_t)$
将每一个LSTM层$L_0,L1,...,L_{m-1}$定义为函数$L_k(M,s_{t-1}^k)=(M_+,s_t^k)$,其中$M$和$M+$为相同维度的特征图。则计算过程如下
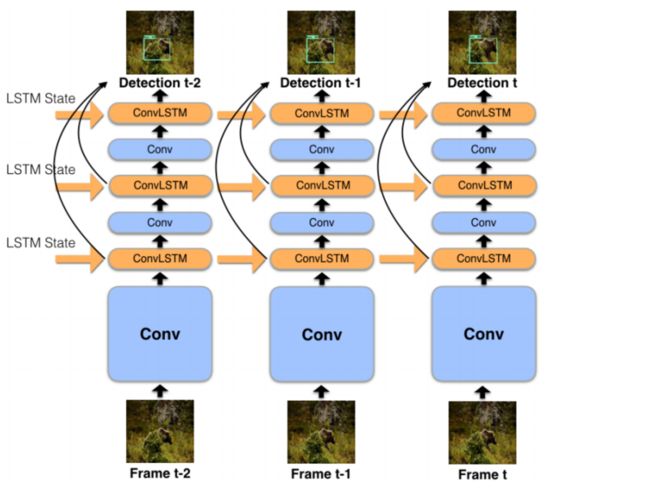
下图给出了这一计算过程的可视化:
将LSTM单元嵌入到检测网络中的哪些层需要仔细探讨,如果嵌入到早期的一些特征层上,会面临很大计算压力。实验部分也给出了证实,嵌入到SSD网络的Conv 13之后是一个较好的选择。SSD网络结构如下表所示:
但是我们还需要考虑如下的嵌入方式:
- 在Conv 13之后嵌入单个LSTM
- 在Conv 13之后嵌入堆叠的多个LSTM
- 在每个特征图后嵌入1个LSTM
先来解答这个问题吧。
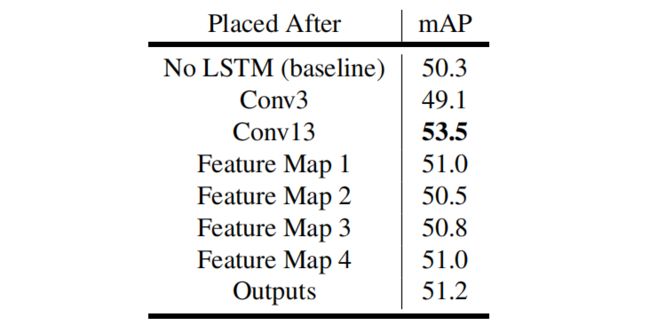
- 单层LSTM放在哪效果最好?下表展示这一问题的实验结果,将单个LSTM放在模型的不同层,可以看出单层LSTM嵌入到Conv 13层是效果最好的。
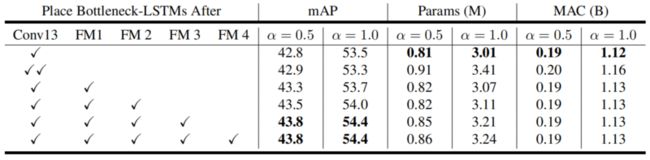
- 多层LSTM如何放置效果最好?由于同时训练多个LSTM非常困难,在逐步添加层的同时,对之前的训练权重进行微调。
由于高层特征的维度更低,增加的计算量并不多。堆叠2层LSTM并没有获得好的收益。
Conv 13,FM1,FM2,FM3之后嵌入LSTM单元是一个不错的选择。
扩展宽度乘数
LSTM计算复杂度高,因为需要计算一系列门。对此,首先想到通道(Channel)降维,给通道一个乘数因子$\alpha$[6]。
定义3个乘数$\alpha_{base},\alpha_{ssd},\alpha_{lstm}$分别控制网络的不同部分。
对于任何MobileNet的输出通道$N$,使其输出为$N\times \alpha_{base}$。
$\alpha_{ssd}$控制所有SSD特征图的通道数,$\alpha_{lstm}$控制LSTM层的特征数。
在实验部分,令$\alpha_{base}=\alpha$,$\alpha_{ssd}=0.5\alpha$,$\alpha_{lstm}=0.25\alpha$。
Bottleneck-LSTM详解
令$M$和$N$分别代表LSTM的输入与输出通道数。由于Convolutional LSTM的具体实现有不同版本[10,11],定义标准Convolutional LSTM如下:
$x_t$和$h_{t-1}$是3D特征图,并将它们按通道连接。$h_t$和$c_t$为输出特征图。
$^jW^k\star X$表示输入为$X$,参数为$W$的深度可分离卷积(Depthwise Separable Convolution),输入通道数为$j$,输出通道数为$k$,$\phi(x)=ReLU(x)$为激活函数,$\circ$表示逐元素乘(Hadamard product)。
注意:使用深度可分离卷积能够有效减少8-9倍计算量,ReLU虽然不常用于LSTM,我们发现不改变映射的边界很重要,因为这里的LSTM是夹在卷积层中间的。
此外,这里的LSTM输出通道数小于输入通道数,我们修改如下公式以压缩特征通道数:
$b_t=\phi(^{(M+N)}W_b^N\star [x_t,h_{t-1}])$
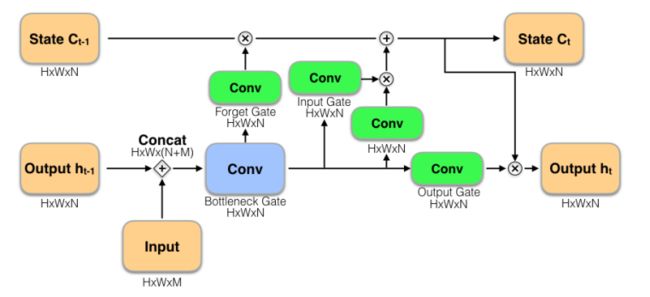
如此$b_t$替换了所有其他门的输入,如下图所示,这被称为Bottleneck-LSTM。有效降低计算量,实际表现效果更好。
令输入特征图空间分辨率为$D_F\times D_F$,深度可分离卷积核大小为$D_K\times D_K$,我们对比一下标准Convolutional LSTM与Bottleneck-LSTM的计算量:
- Convolutional LSTM(GRU是其计算量的3/4)
$4(D_K^2\cdot (M+N)\cdot D_F^2+(M+N)\cdot N\cdot D_F^2)$
- Bottleneck-LSTM
$D_K^2\cdot (M+N)\cdot D_F^2+(M+N)\cdot N\cdot D_F^2+4(D_K^2\cdot N\cdot D_F^2+N^2\cdot D_F^2)$
设$D_K=3$,令$k=\frac{M}{N}$。$k>\frac{1}{3}$时,Bottleneck-LSTM就可以超过Convolutional LSTM,$k=4$时,Bottleneck-LSTM成为不二之选。
算法实现细节
训练与评估的数据集是ImageNet VID 2015。LSTM按时序展开10步,即10帧图像参与LSTM时序建模。
训练两种乘数模型,分别是$\alpha=1$和$\alpha=0.5$。
$\alpha=1$时,输入图像分辨率为$320\times 320$,学习率为0.003;$\alpha=0.5$时,输入图像分辨率为$256\times 256$,学习率为0.002。
困难负样本挖掘与数据增强策略参考文献[4]。10个负样本对应1个正样本,且负样本损失乘以0.3。
为了应对过拟合,训练网络时采用两个阶段步骤。
首先,不嵌入LSTM网络,微调SSD网络。然后冻结主干网络参数,直到Conv 13层,且包括Conv 13层,接着,嵌入LSTM网络,完成之后的训练过程。
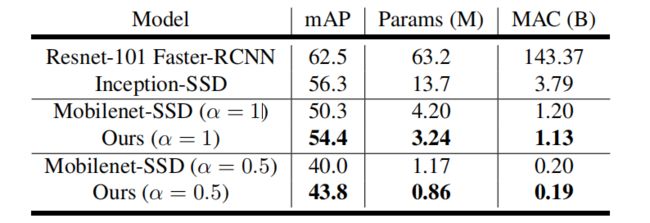
最后,给出一张与单幅图像目标检测器的对比结果,进步还是比较可观,当然,也并没有质的飞跃==。
参考
[1] R. Girshick, J. Donahue, T. Darrell, and J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014. 1, 2
[2] K. He, X. Zhang, S. Ren, and J. Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. In ECCV, 2014. 1
[3] J. Dai, Y. Li, K. He, and J. Sun. R-fcn: Object detection via region-based fully convolutional networks. In NIPS, 2016. 1, 2
[4] W. Liu, D. Anguelov, D. Erhan, C. Szegedy, S. Reed, C.-Y. Fu, and A. C. Berg. Ssd: Single shot multibox detector. In ECCV, 2016. 1, 2, 5
[5] S. Ren, K. He, R. Girshick, and J. Sun. Faster r-cnn: Towards real-time object detection with region proposal networks. In NIPS, 2015. 1, 2
[6] A. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang, T. Weyand, M. Andreetto, and H. Adam. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861, 2017. 1, 3, 4
[7] X. Zhang, X. Zhou, M. Lin, and J. Sun. Shufflenet: An extremely efficient convolutional neural network for mobile devices. arXiv preprint arXiv:1707.01083, 2017. 1, 3
[8] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199, 2013. 1
[9] S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural Computation, 9(8):1735–1780, 1997. 3
[10] V. Patraucean, A. Handa, and R. Cipolla. Spatio-temporal video autoencoder with differentiable memory. arXiv preprint arXiv:1511.06309, 2015. 3, 4
[11] X. Shi, Z. Chen, H. Wang, D. Yeung, W. Wong, and W. Woo. Convolutional lstm network: A machine learning approach for precipitation nowcasting. In NIPS, 2015. 3, 4