二叉树的四种遍历(基础知识)

二叉树(Binary Tree)是n(n>=0)个结点的有限集合，该集合可以为空，或者由一个根几点和俩颗互不相交的子树组成

 

 

特点

• 每个结点最多有两棵子树，故不存在度大于2的结点（要和图的度分清，图是有出度和入度之分的，这里的度就是它的儿子结点）
• 左子树和右子树是有顺序的，次序不能任意颠倒
• 即使树中某结点只有一棵子树，也要区分是左子树还是右子树

 

 

五种基本形态

• 空二叉树
• 只有一个根节点
• 根节点只有左子树
• 根节点只有右子树
• 根节点既有左子树又有右子树

 

特殊二叉树

• 斜树：所有结点都只有左子树的二叉树叫左斜树，对应有右斜树，统称为斜树

• 满二叉树：所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上的二叉树

  • 叶子只能出现在最下一层，否则不平衡
  • 非叶子节点的度一定是2
  • 同样深度的二叉树，满二叉树的结点个数最多，叶子数最多

  

 

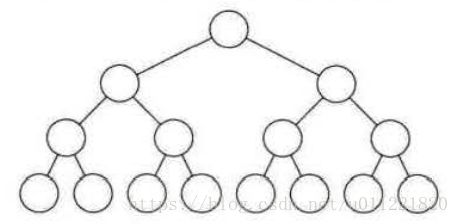
完全二叉树： 对一棵具有n个结点的二叉树按层序编号，如果编号为i(1≤i≤n)i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树

• 叶子结点只能出现在最下两层
• 最下层的叶子一定集中在左部连续位置
• 倒数二层，若有叶子结点，一定都在右部连续位置
• 如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况

二叉树的性质

• 在二叉树的第i层上至多有2i−12i−1个结点(i≥1)(i≥1)
• 深度为k的二叉树至多有2k−12k−1个结点(k≥1)(k≥1)
• 对任何一棵二叉树T， 如果其终端结点数为n0n0， 度为2的结点树为n2n2， 则n0=n2+1n0=n2+1
• 具有n个结点的完全二叉树的深度为⌊log2n⌋+1⌊log2n⌋+1 (⌊x⌋表示不大于x的最大整数)(⌊x⌋表示不大于x的最大整数)
• 如果对一棵具有n个结点的完全二叉树(其深度为⌊log2n⌋+1⌊log2n⌋+1)的结点按层序编号(从第1层到第⌊log2n⌋+1⌊log2n⌋+1层，每层从左到右)，对任一结点 i(1≤i≤n)i(1≤i≤n)有： 
  • 如果 i = 1， 则结点i是二叉树的根，无双亲；如果i>1i>1, 则其双亲是结点⌊i/2⌋⌊i/2⌋
  • 如果 2i>n2i>n， 则结点i无左孩子(结点i为叶子结点); 否则即2i≤n2i≤n时其左孩子是结点2i2i
  • 如果2i+1>n2i+1>n， 则结点i无右孩子；否则2i+1≤n2i+1≤n时， 其右孩子是结点2i+1

 

二叉树的存储结构

二叉树顺序存储结构

顺序存储结构一般只用于 完全二叉树，否则会造成空间浪费

二叉链表(链式存储结构)

二叉树每个结点最多有两个孩子，故结点结构为一个数据域和两个指针域

typedef struct node;
typedef node *tree;
struct node
{
	int data;
	tree L, R;
};

 

遍历二叉树

二叉树的遍历(traversing binary tree)是指从根节点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。 由前序和后序无法得到唯一二叉树

前序遍历

规则是若二叉树为空，则空操作返回，否则先返回根节点，然后前序遍历左子树，再前序遍历右子树。下图遍历顺序为ABDGHCEIF

 

中序遍历

规则是若树为空，则空操作返回，否则从根节点开始(注意并不是先访问根节点)，中序遍历根节点的左子树，然后是访问根节点，最后中序遍历右子树。下图遍历顺序为GDHBAEICF

 

后序遍历

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根节点。下图遍历顺序为GHDBIEFCA

 

层序遍历

规则是若树为空，则空操作返回，否则从树的第一层，也就是根节点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。下图遍历顺序为ABCDEFGHI

 

非递归实现四种遍历

#include
#include
#include
#include
#include
#include