计算智能-蚁群算法
一、蚁群算法原理介绍
定义:
蚁群算法(AG)是一种模拟蚂蚁觅食行为的模拟优化算法,它是由意大利学者Dorigo M等人于1991年首先提出,并首先使用在解决TSP(旅行商问题)上。
之后,又系统研究了蚁群算法的基本原理和数学模型.
基本流程:
用一只蚂蚁的行走路径代表一个可行解;
1、确定迭代周期;
2、确定蚂蚁数;
3、对每只蚂蚁;
3.a、随机选择起点;
3.b、选择下一步;
3.b.a、根据所有与当前节点有关的路径上的信息素多少,决定下一步,一般信息素越多,选择该路径的概率越高;
3.b.b、蚂蚁有一定概率选择错误,即随机选择下一步;
3.c、选择后,在选择的路径上按照一定规则留下一定量的信息素;
3.d、最终的蚂蚁路径就是本次搜索的最佳路径;
4、等待周期结束;
二、主要源代码
%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 150; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
figure;
while iter <= iter_max
fprintf('迭代第%d次\n',iter);
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
% figure;
%最佳路径的迭代变化过程
[Shortest_Length,index] = min(Length_best(1:iter));
Shortest_Route = Route_best(index,:);
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
pause(0.3);
iter = iter + 1;
Table = zeros(m,n);
% end
end
三、结果分析
1、通过更改信息素挥发因子的值来观察其迭代情况
(1)当alpha = 1;beta = 5; rho = 0.1时

最短距离:27799.6554
最短路径:8 31 22 43 49 4 10 41 19 2 25 14 34 15 28 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 5 9 7 38 12 33 44 39 29 21 32 48 45 23 1 42 20 8
(2)当alpha = 1;beta = 5; rho = 0.2时
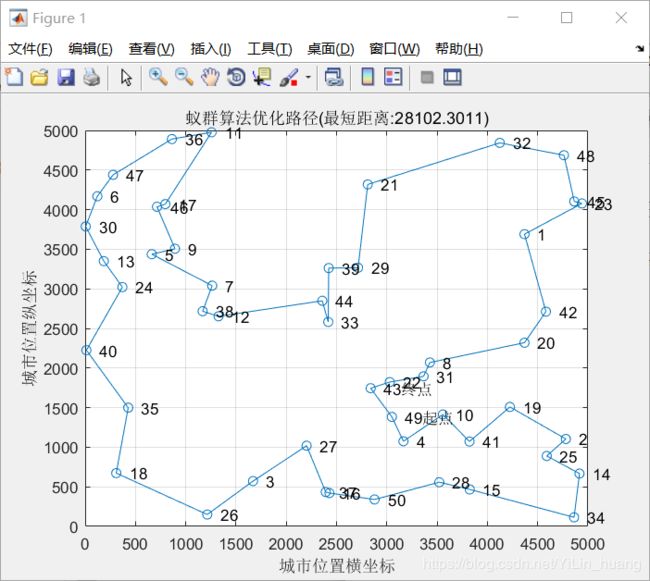
最短距离:28102.3011
最短路径:49 4 10 41 19 2 25 14 34 15 28 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 9 5 7 38 12 44 33 39 29 21 32 48 45 23 1 42 20 8 31 22 43 49
(3)当alpha = 1;beta = 5; rho = 0.5时
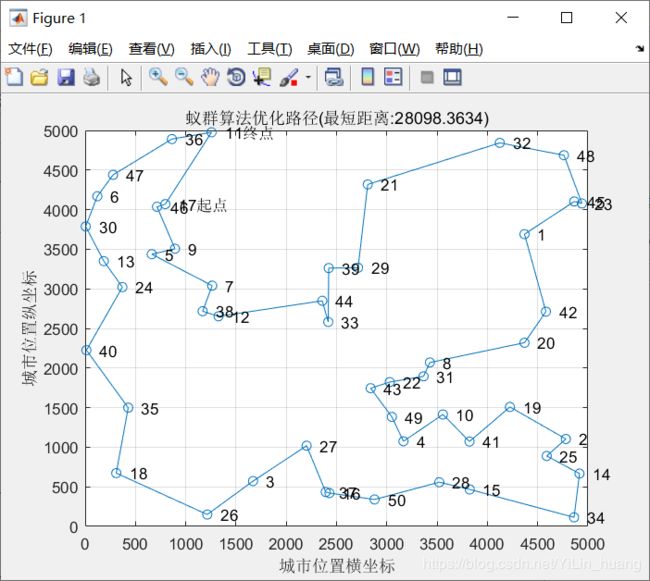
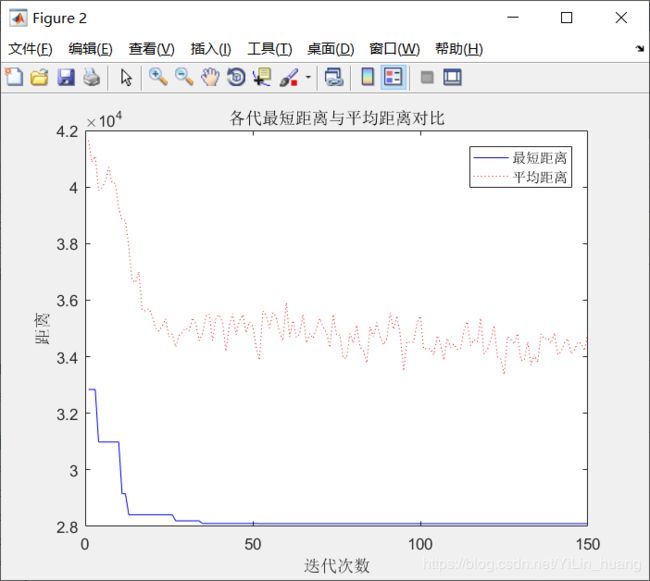
最短距离:28098.3634
最短路径:17 46 9 5 7 38 12 44 33 39 29 21 32 48 23 45 1 42 20 8 31 22 43 49 4 10 41 19 2 25 14 34 15 28 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17
(4)当alpha = 1;beta = 5; rho = 0.7时
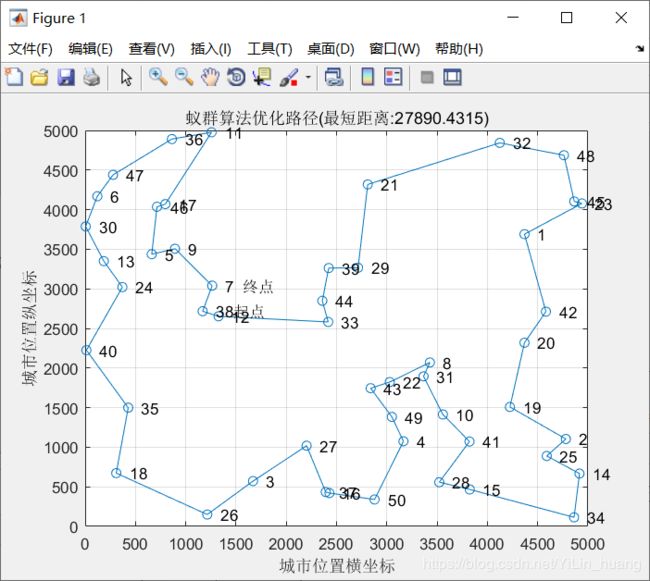
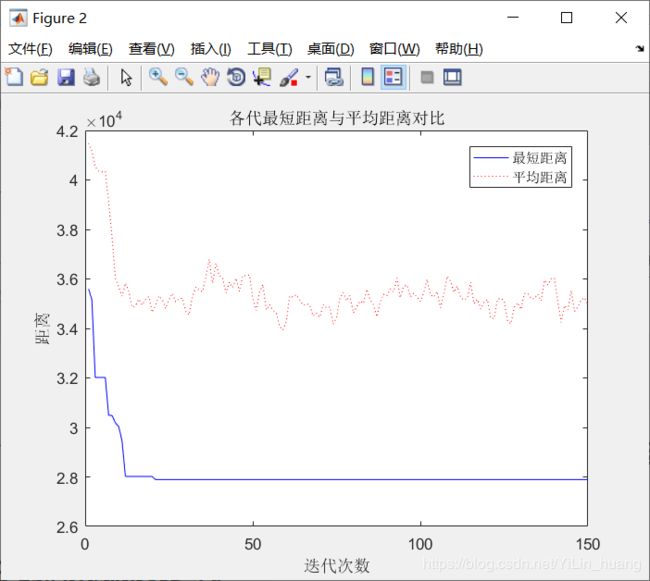
最短距离:27890.4315
最短路径:38 12 33 44 39 29 21 32 48 45 23 1 42 20 19 2 25 14 34 15 28 41 10 31 8 22 43 49 4 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 5 9 7 38
2、通过更改信息素重要程度因子的值来观察其迭代情况
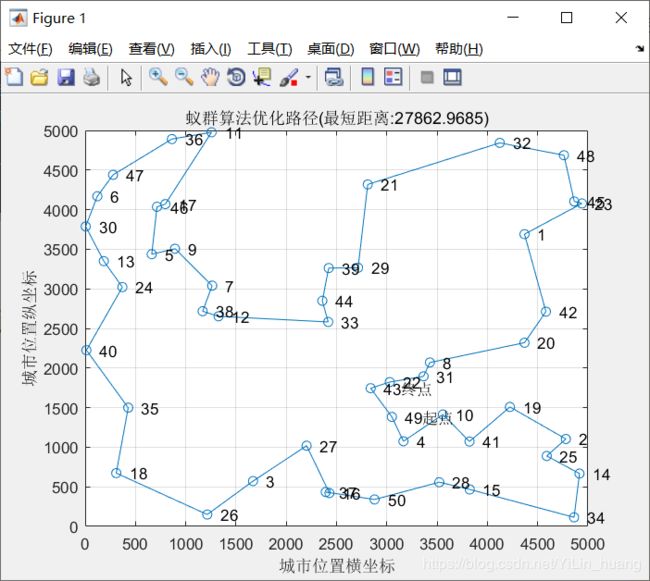
(1)当alpha = 1;beta = 5; rho = 0.2时
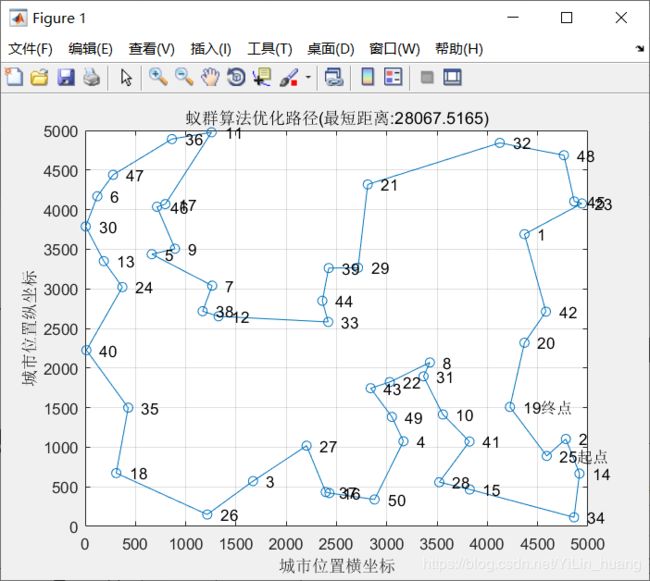

最短距离:28067.5165
最短路径:25 2 14 34 15 28 41 10 31 8 22 43 49 4 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 9 5 7 38 12 33 44 39 29 21 32 48 45 23 1 42 20 19 25
(2)当alpha = 2;beta = 5; rho = 0.2时
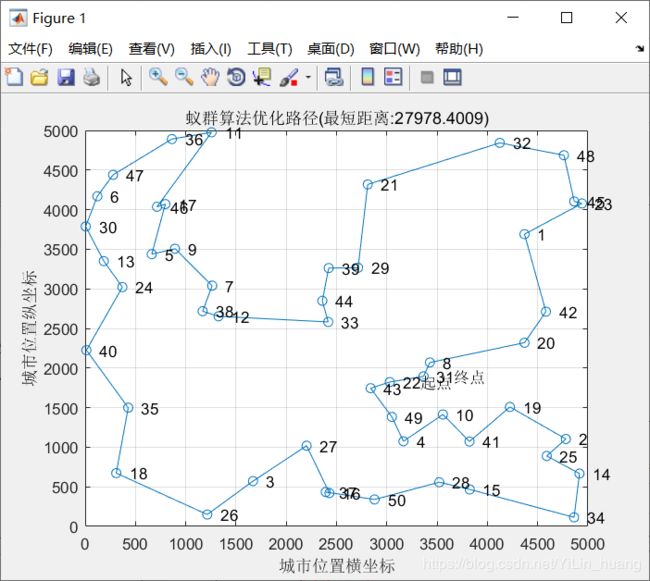
最短距离:27978.4009
最短路径:22 43 49 4 10 41 19 2 25 14 34 15 28 50 37 16 27 3 26 18 35 40 24 13 30 6 47 36 11 46 17 5 9 7 38 12 33 44 39 29 21 32 48 45 23 1 42 20 8 31 22
(3)当alpha = 5;beta = 5; rho = 0.2时
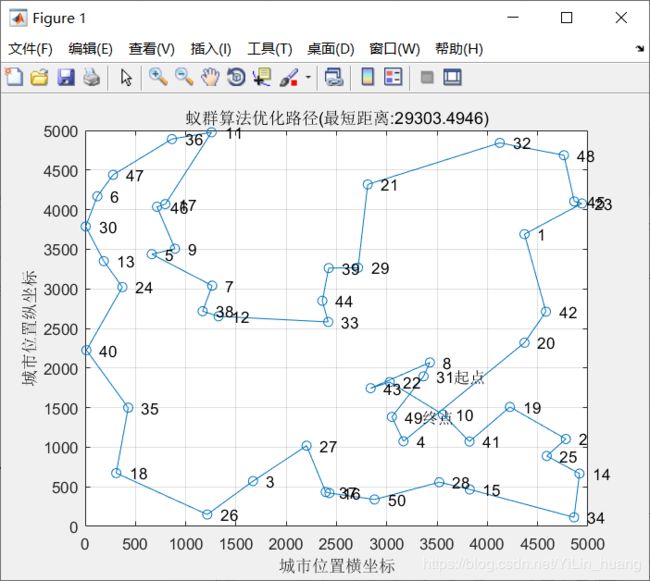
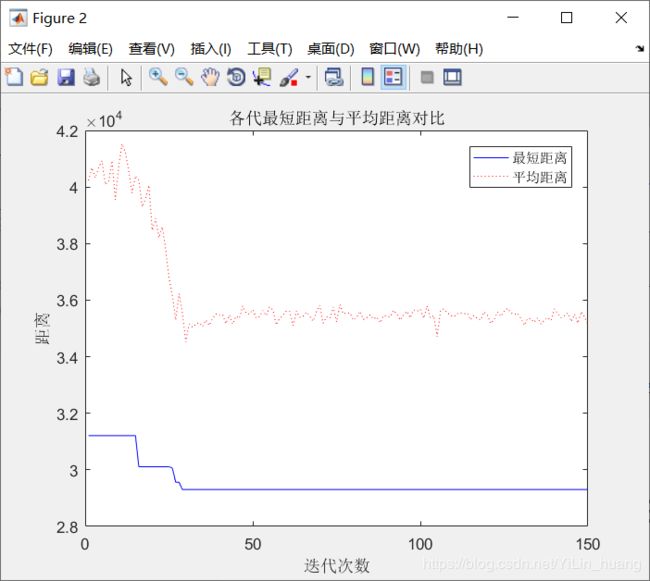
最短距离:29303.4946
最短路径:31 8 43 22 10 41 19 2 25 14 34 15 28 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 9 5 7 38 12 33 44 39 29 21 32 48 45 23 1 42 20 4 49 31
3、通过更改启发函数重要程度因子的值来观察其迭代情况
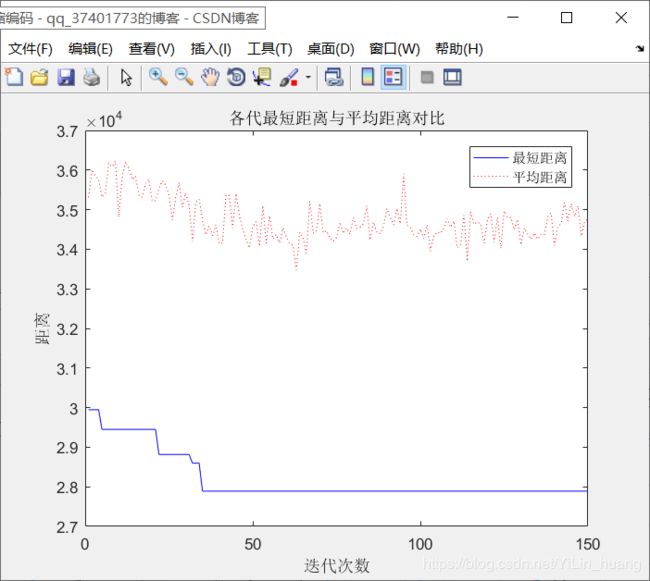
(1)当alpha = 1;beta = 5; rho = 0.2时
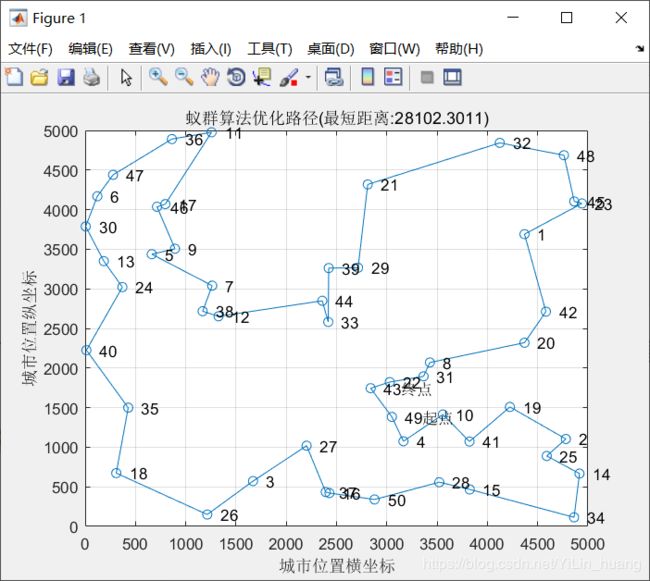
最短距离:28102.3011
最短路径:49 4 10 41 19 2 25 14 34 15 28 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 9 5 7 38 12 44 33 39 29 21 32 48 45 23 1 42 20 8 31 22 43 49
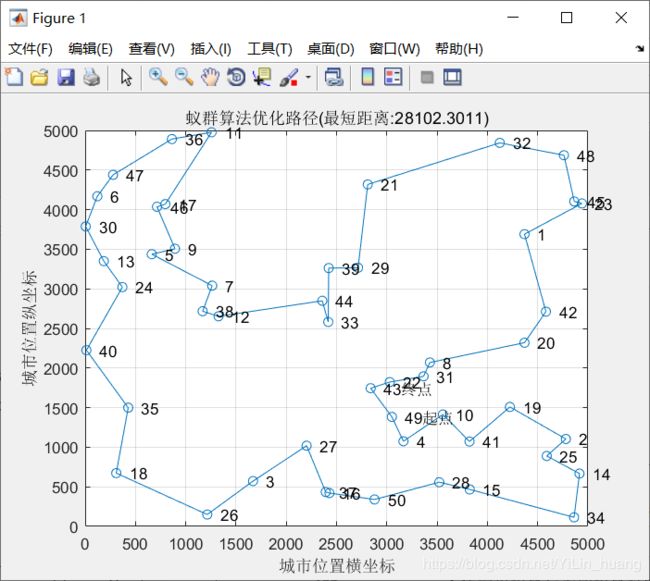
(2)当alpha = 1;beta = 10; rho = 0.2时
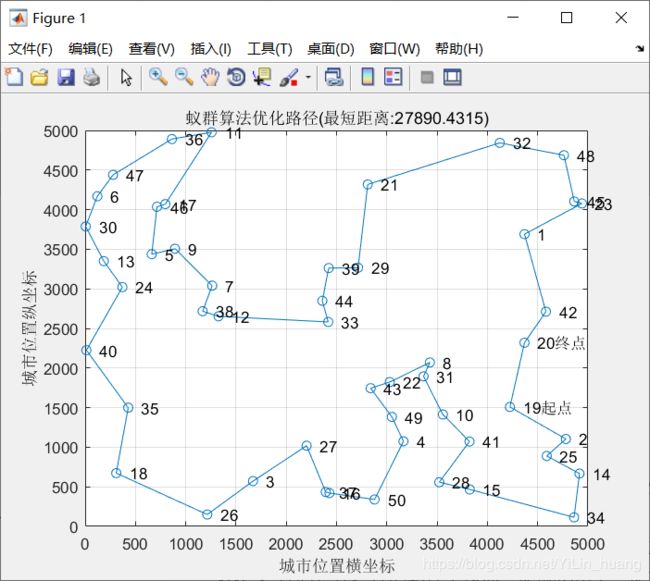
最短距离:27890.4315
最短路径:19 2 25 14 34 15 28 41 10 31 8 22 43 49 4 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 5 9 7 38 12 33 44 39 29 21 32 48 45 23 1 42 20 19
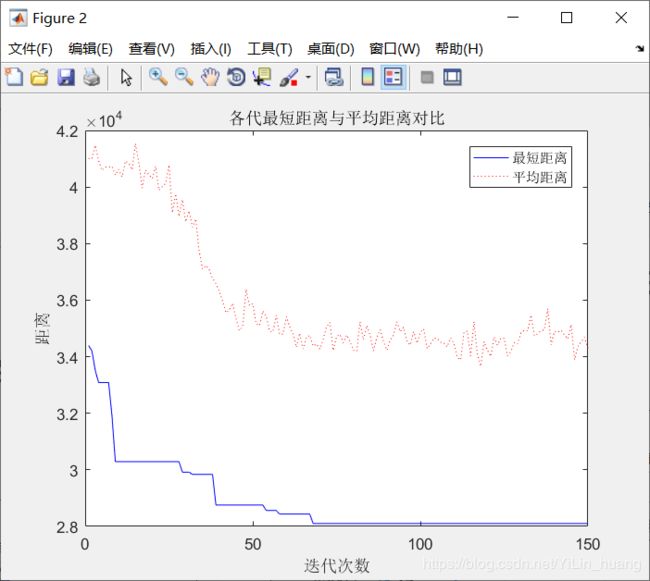
(3)当alpha = 1;beta =20; rho = 0.2时
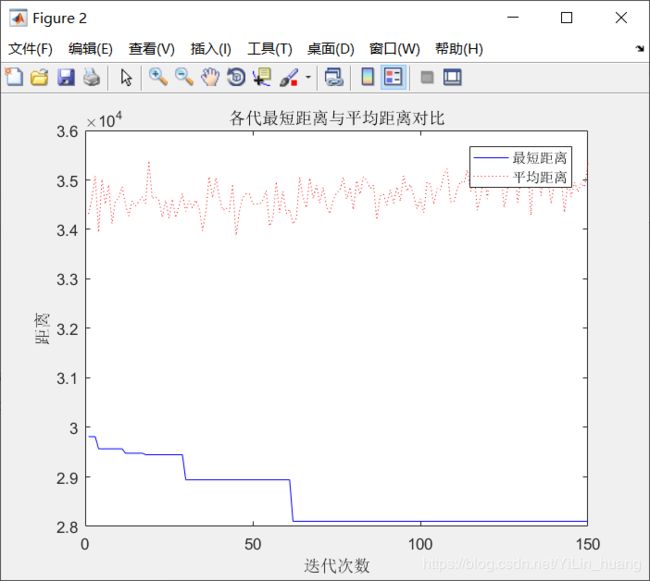
最短距离:28102.3011
最短路径:49 4 10 41 19 2 25 14 34 15 28 50 16 37 27 3 26 18 35 40 24 13 30 6 47 36 11 17 46 9 5 7 38 12 44 33 39 29 21 32 48 45 23 1 42 20 8 31 22 43 49
四、结论
1、通过更改信息素挥发因子的值来观察其迭代情况
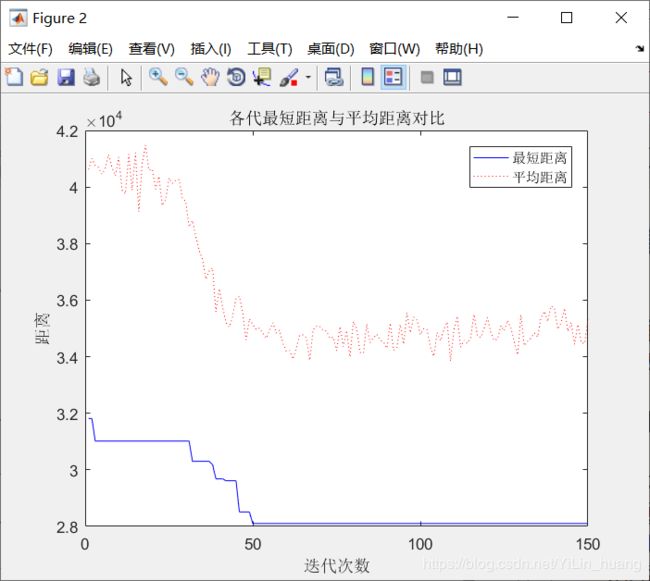
rho 影响蚂蚁个体之间互相影响的强弱,关系到算法的全局搜索能力和收敛速度。他的挥发速度越快,迭代次数就会越快,反之,则减慢。
信息素挥发因子的不断增加会使收敛速度会加快,每轮迭代的计算量越大,经过少次的迭代就可以得到最优路线。从实验结果来看,rho值越趋向1,他收敛就越快。
2、通过更改信息素重要程度因子的值来观察其迭代情况
alpha = 1时最短距离收敛的比较快,收敛的速度随着alpha的值不断的增加而增加。但是在值从2变到5时他的收敛速度并没有发生太大的改变,由此可见,值为2的时候为其优值。
3、通过更改启发函数重要程度因子的值来观察其迭代情况
beta 是指的期望启发因子,它反映的是启发式信息在影响蚁群搜索的过程当中的相对重要度,它的大小影响着蚁群在整个寻优的过程中的先验性和确定性。beta 值越大,蚁群就越容易选择局部较短路径,容易得到局部的相对最优。beta 越小,蚂蚁越倾向于根据信息素浓度确定路径,算法收敛越快。beta值从1升到5时,算法收敛速度加快,但是从5升到20的时候收敛速度反而是下降的,他的最优值应是在5左右。
实验小结
本次实验通过实验分析,分别研究信息素挥发因子、信息素重要程度因子、启发函数重要程度因子的值对蚁群算法的结果产生的影响。可以得到,这三种因子都对实验结果有不同程度的影响,在设置参数的时候应该要谨慎使用,应该通过反复实验来确定其范围,得到最优解。