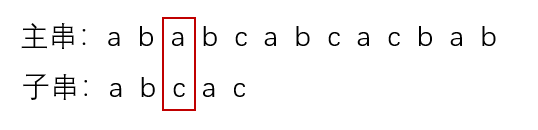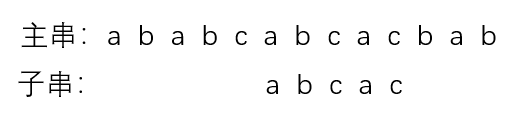【数据结构·考研】KMP算法

子串的定位操作通常称为串的模式匹配，它求的是子串（常称模式串）在主串中的位置。

我们平常遇到类似模式匹配的问题需求时，第一反应想到的就是朴素模式匹配算法（暴力匹配）。

朴素模式匹配算法：给定一个主串S和模式串T，从主串S的第pos个字符起，与模式串的第一个字符比较，若相等，则继续逐个比较后序字符；否则从主串pos位置的下一个字符起，重新和模式串的字符比较。以此类推，直至模式串T中的每个字符依次和主串S中的一个连续字符序列相等，则匹配成功。函数返回与模式串T中第一个字符相等的字符在主串S中的下标。匹配不成功返回-1。

朴素模式匹配算法实现：

主串S：ababcabcacbab      

模式串T：abcac

#include
#include
using namespace std;

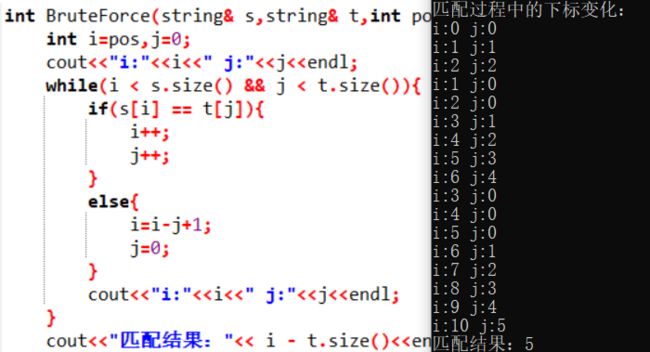
int BruteForce(string& s,string& t,int pos){
	int i=pos,j=0;
	while(i < s.size() && j < t.size()){
		if(s[i] == t[j]){
			i++;
			j++;
		}
		else{
			i=i-j+1;
			j=0;
		}
	}
	if(j == t.size()) return i - t.size();
	else return -1;
} 

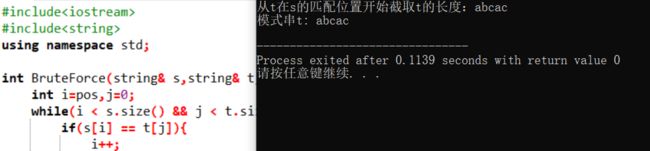
int main(){
	string s="ababcabcacbab";
	string t="abcac";
	cout<<"从t在s的匹配位置开始截取t的长度：";
	cout<

运行结果如下：

匹配过程中i，j的下标变化：

j值增加到5后结束循环，与模式串长度相同，返回结果。

最坏时间复杂度：O(m*n)。

空间复杂度：O(1)。

暴力匹配算法的缺点很明显，效率实在太低，每一轮只能老老实实地把模式串右移一位，实际上做了很多无谓的比较。

如何有效利用已匹配的前缀来消除主串指针的回溯，人们引出了KMP算法。

KMP算法利用比较过的信息，i指针不回溯，仅将子串向后滑动到一个合适的位置，并从这个位置开始和主串进行比较，这个合适的位置仅与子串本身结构有关，而与主串无关。

在正式理解KMP算法之前，我们来弄清几个概念：

前缀：除最后一个字符外，字符串的所有头部子串

后缀：除第一个字符外，字符串的所有尾部子串

部分匹配值：字符串前缀和后缀的最长相等前后缀长度

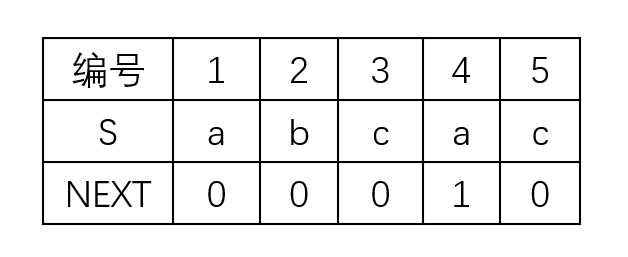
例如模式串“abcac”：

①'a'的前缀和后缀都为空集，最长相等前后缀长度为0。

②'ab'的前缀为{a}，后缀为{b},最长相等前后缀长度为0。

③'abc'的前缀为{a,ab}，后缀为{c,bc},最长相等前后缀长度为0。

以此类推'abca'最长相等前后缀长度为1，即a。前缀{a,ab,abc}，后缀{a,ca,bca}。

'abcac'的最长相等前后缀长度为0。

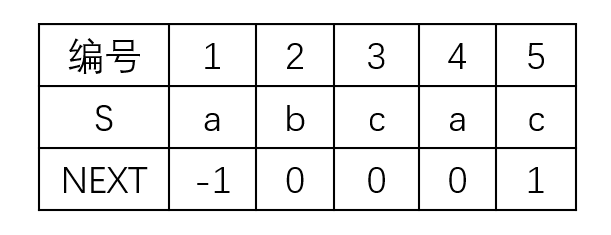
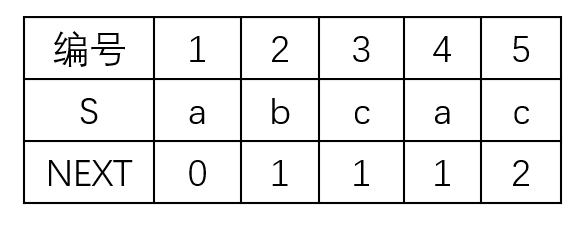
至此我们得到模式串“abcac”的部分匹配值数组：

我们称其为next数组。

当然在我们手撕next数组时，直接去找最长的相等前后缀长度即可，不需要将前后缀一一列举。

下面用next数组进行字符串匹配：

①第一趟匹配过程：

发现c与a不匹配，最后一个匹配字符b对应的部分匹配值为0，按照下面公式算出子串需要后移的位数：

移动位数 = 已匹配的字符数 - 对应的部分匹配值

2 - next[2] = 0，所以子串向后移动2位进行第二趟匹配。

②第二趟匹配过程：

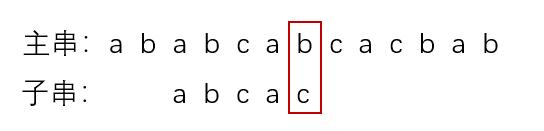
发现c与b不匹配，4 - next[4] = 3，子串向后移动三位，进行第三趟匹配。

③第三趟匹配：

匹配成功，整个匹配过程中主串始终没有回退。

其实KMP就是把我们人为的偷懒思想用数学的方式实现。

例如说第二趟过程，当我们发现b与c不匹配时，按照朴素模式匹配算法，我们要将模式串的首个字符滑动到主串的第四个字符处，这样模式串首字符与回溯后后面的字符b、c相比较都是徒劳的，人为的偷懒让我们期望模式串可以直接在主串的第六个字符对齐，主串就可以从当前指针位置继续往后匹配，主串指针不需要回退，许多不必要的比较也都被跳过。

而这一过程就是通过前缀后缀计算出的next数组来得到的。

在第二趟的比较的过程中，主串指针i向前移动了5个下标后指向了第七个字符，此时它发现b与c不同，检查next数组发现模式串的最长相等前后缀长度为1，那么我只要把模式串的头部移到我这一趟匹配成功的最后一个字符处即可，这样a与a是相同的，直接跳过中间徒劳的滑动；主串也可以接着自己当前的位置继续向后匹配。

这个需要移动的距离是3，就可以通过最后一个匹配成功字符的下标减去对应next数组的值(最后一个匹配成功字符所对应最长相等前后缀长度)来得到。4-1=3。这个公式清晰的体现出前后缀思想在next数组形成中的作用。

我们常常可以看到两种next数组的写法。

之前的next数组写法每当匹配失败时，主串指针和模式串指针都走到了失败的字符处，想要知道模式串下一次KMP匹配要滑动的长度，还需要去看前一个字符也就是最后一个成功字符的next数组值和j的下标值，这样使用起来有一点不方便。

所以我们把next数组整个右移一位，在第一位补 -1。这是next数组常见写法其一。

原先的移动位数公式就演变为 Move = (j - 1) - next[ j ]

这样移动后的j的下标变为j - Move = j - ((j - 1) - next[ j ]) = next[ j ] + 1

为了使公式更加简洁、计算简单，将next数组整体+1。也就变成另一种形态的next数组。

虽然不同的写法变来变去，但是理解几种next数组的由来后，就变得简单多了。

下面给出next数组的实现：

#include
#include
#include
using namespace std;

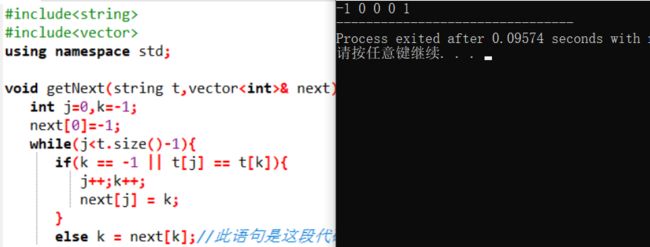
void getNext(string& t,vector& next){
   int j=0,k=-1;
   next[0]=-1;
   while(j next(t.size());
	getNext(t,next);
	for(int i=0;i

运行结果：

有了next数组，KMP算法就要简单得多了。

#include
#include
#include
using namespace std;

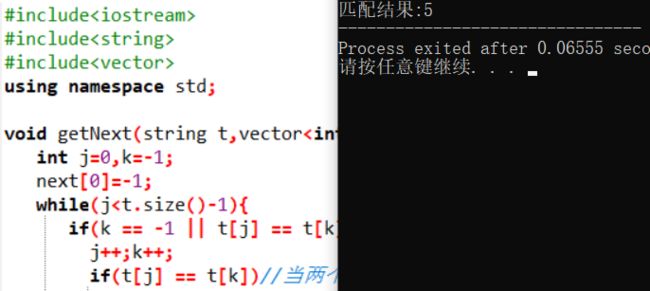
void getNext(string& t,vector& next){
   int j=0,k=-1;
   next[0]=-1;
   while(j& next){
   int i=0,j=0;
   getNext(t,next);
   while(i < s.size() && j < t.size()){
      if(j == -1 || s[i]==t[j]){
         i++;
         j++;
      }
      else j=next[j]; //j回退
   }
   if(j >= t.size()) return i-t.size(); //匹配成功，返回子串的位置
   else return -1; 
}

int main(){
	string s="ababcabcacbab";
	string t="abcac";
	vector next(t.size());
	cout<<"匹配结果:"<

KMP算法是改进的模式串匹配算法，而还有next数组的改进版next数组，有时又叫nextval。

#include
#include
#include
using namespace std;

void getNext(string& t,vector& next){
   int j=0,k=-1;
   next[0]=-1;
   while(j& next){
   int i=0,j=0;
   getNext(t,next);
   while(i < s.size() && j < t.size()){
      if(j == -1 || s[i]==t[j]){
         i++;
         j++;
      }
      else j=next[j]; //j回退
   }
   if(j >= t.size()) return i-t.size(); //匹配成功，返回子串的位置
   else return -1; 
}

int main(){
	string s="ababcabcacbab";
	string t="abcac";
	vector next(t.size());
	cout<<"匹配结果:"<

本文图例及部分算法思想参考博主DK丶S的文章，具体细节仍旧没有完全搞明白。

KMP算法—终于全部弄懂了