keras对猫、狗数据集进行分类(三)
目录
keras对猫、狗数据集进行分类(一)
keras对猫、狗数据集进行分类(二)
keras对猫、狗数据集进行分类(三)
数据集:关注下方公众号,发送 猫狗数据集 进行获取
![]()
使用已训练模型对猫狗图片进行测试,以及可视化模型训练过程。
示例代码:
# # 可视化卷积神经网络
#
# 人们常说,深度学习模型是“黑盒子”,学习表示难以提取并以人类可读的形式呈现。
# 虽然对于某些类型的深度学习模型来说这是部分正确的,但对于小行星来说绝对不是这样。
# 由convnets学习的表示非常适合可视化,这在很大程度上是因为它们是视觉概念的代表_。
# *可视化中间信号输出(“中间激活”)。 这有助于理解连续的convnet层如何转换其输入,并首先了解各个convnet过滤器的含义。
# *可视化convnets过滤器。 这有助于准确理解convnet中每个过滤器可以接受的视觉模式或概念。
# ## 可视化中间激活
#
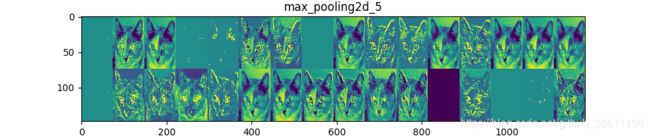
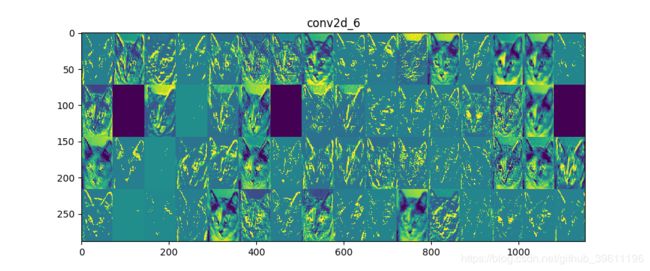
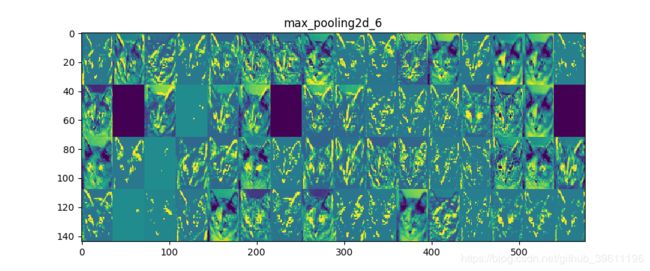
# 可视化中间激活包括在给定特定输入的情况下显示由网络中的各种卷积和池化层输出的特征图
# (层的输出通常称为“激活”,激活函数的输出)。 这给出了如何将输入分解为网络学习的不
# 同过滤器的视图。 我们想要可视化的这些要素图有3个维度:宽度,高度和深度(通道)。
# 每个通道编码相对独立的特征,因此可视化这些特征图的正确方法是通过独立地绘制每个通道的内容,作为2D图像。
from keras.models import load_model
# 使用前面训练得到的模型
model = load_model('cats_and_dogs_small_2.h5')
print(model.summary())
img_path = './cats_and_dogs_small/test/cats/cat.1700.jpg'
# 将图像预处理成4D张量
from keras.preprocessing import image
import numpy as np
img = image.load_img(img_path, target_size=(150, 150))
img_tensor = image.img_to_array(img)
img_tensor = np.expand_dims(img_tensor, axis=0)
img_tensor /= 255.
# shape (1, 150, 150, 3)
print(img_tensor.shape)
import matplotlib.pyplot as plt
plt.imshow(img_tensor[0])
plt.show()
# 为了提取我们想要查看的特征图,我们将创建一个Keras模型,该模型将批量图像作为输入,
# 并输出所有卷积和池化层的激活。 为此,我们将使用Keras类`Model`。 使用两个参数
# 来实例化“模型”:输入张量(或输入张量列表)和输出张量(或输出张量列表)。 生成的类
# 是Keras模型,就像您熟悉的`Sequential`模型一样,将指定的输入映射到指定的输出。
from keras import models
# 提取前8层的输出
layer_outputs = [layer.output for layer in model.layers[:8]]
# 在给定模型输入的情况下,创建将返回这些输出的模型
activation_model = models.Model(inputs=model.input, outputs=layer_outputs)
# 当输入图像输入时,此模型返回原始模型中图层激活的值。 这是您第一次在本书中遇到多输出模型:
# 到目前为止,您所看到的模型只有一个输入和一个输出。 在一般情况下,模型可以具有任意数量的输入和输出。
# 这个有一个输入和8个输出,每层激活一个输出。
# 这将返回5个Numpy数组的列表:
# 每层激活一个数组
activations = activation_model.predict(img_tensor)
# 这是我们猫图像输入的第一个卷积层的激活
first_layer_activation = activations[0]
print(first_layer_activation.shape)
# 这是一个包含32个频道的148x148功能图。 让我们尝试可视化第三个频道:
import matplotlib.pyplot as plt
plt.matshow(first_layer_activation[0, :, :, 3], cmap='viridis')
plt.show()
# This channel appears to encode a diagonal edge detector. Let's try the 30th channel -- but note that your own channels may vary, since the
# specific filters learned by convolution layers are not deterministic.
# In[9]:
plt.matshow(first_layer_activation[0, :, :, 30], cmap='viridis')
plt.show()
# This one looks like a "bright green dot" detector, useful to encode cat eyes. At this point, let's go and plot a complete visualization of
# all the activations in the network. We'll extract and plot every channel in each of our 8 activation maps, and we will stack the results in
# one big image tensor, with channels stacked side by side.
# In[10]:
import keras
# These are the names of the layers, so can have them as part of our plot
layer_names = []
for layer in model.layers[:8]:
layer_names.append(layer.name)
images_per_row = 16
# Now let's display our feature maps
for layer_name, layer_activation in zip(layer_names, activations):
# This is the number of features in the feature map
n_features = layer_activation.shape[-1]
# The feature map has shape (1, size, size, n_features)
size = layer_activation.shape[1]
# We will tile the activation channels in this matrix
n_cols = n_features // images_per_row
display_grid = np.zeros((size * n_cols, images_per_row * size))
# We'll tile each filter into this big horizontal grid
for col in range(n_cols):
for row in range(images_per_row):
channel_image = layer_activation[0,
:, :,
col * images_per_row + row]
# Post-process the feature to make it visually palatable
channel_image -= channel_image.mean()
channel_image /= channel_image.std()
channel_image *= 64
channel_image += 128
channel_image = np.clip(channel_image, 0, 255).astype('uint8')
display_grid[col * size: (col + 1) * size,
row * size: (row + 1) * size] = channel_image
# Display the grid
scale = 1. / size
plt.figure(figsize=(scale * display_grid.shape[1],
scale * display_grid.shape[0]))
plt.title(layer_name)
plt.grid(False)
plt.imshow(display_grid, aspect='auto', cmap='viridis')
plt.show()
# A few remarkable things to note here:
#
# * The first layer acts as a collection of various edge detectors. At that stage, the activations are still retaining almost all of the
# information present in the initial picture.
# * As we go higher-up, the activations become increasingly abstract and less visually interpretable. They start encoding higher-level
# concepts such as "cat ear" or "cat eye". Higher-up presentations carry increasingly less information about the visual contents of the
# image, and increasingly more information related to the class of the image.
# * The sparsity of the activations is increasing with the depth of the layer: in the first layer, all filters are activated by the input
# image, but in the following layers more and more filters are blank. This means that the pattern encoded by the filter isn't found in the
# input image.
#
# We have just evidenced a very important universal characteristic of the representations learned by deep neural networks: the features
# extracted by a layer get increasingly abstract with the depth of the layer. The activations of layers higher-up carry less and less
# information about the specific input being seen, and more and more information about the target (in our case, the class of the image: cat
# or dog). A deep neural network effectively acts as an __information distillation pipeline__, with raw data going in (in our case, RBG
# pictures), and getting repeatedly transformed so that irrelevant information gets filtered out (e.g. the specific visual appearance of the
# image) while useful information get magnified and refined (e.g. the class of the image).
#
# This is analogous to the way humans and animals perceive the world: after observing a scene for a few seconds, a human can remember which
# abstract objects were present in it (e.g. bicycle, tree) but could not remember the specific appearance of these objects. In fact, if you
# tried to draw a generic bicycle from mind right now, chances are you could not get it even remotely right, even though you have seen
# thousands of bicycles in your lifetime. Try it right now: this effect is absolutely real. You brain has learned to completely abstract its
# visual input, to transform it into high-level visual concepts while completely filtering out irrelevant visual details, making it
# tremendously difficult to remember how things around us actually look.
# ## Visualizing convnet filters
#
#
# Another easy thing to do to inspect the filters learned by convnets is to display the visual pattern that each filter is meant to respond
# to. This can be done with __gradient ascent in input space__: applying __gradient descent__ to the value of the input image of a convnet so
# as to maximize the response of a specific filter, starting from a blank input image. The resulting input image would be one that the chosen
# filter is maximally responsive to.
#
# The process is simple: we will build a loss function that maximizes the value of a given filter in a given convolution layer, then we
# will use stochastic gradient descent to adjust the values of the input image so as to maximize this activation value. For instance, here's
# a loss for the activation of filter 0 in the layer "block3_conv1" of the VGG16 network, pre-trained on ImageNet:
# In[12]:
from keras.applications import VGG16
from keras import backend as K
model = VGG16(weights='imagenet',
include_top=False)
layer_name = 'block3_conv1'
filter_index = 0
layer_output = model.get_layer(layer_name).output
loss = K.mean(layer_output[:, :, :, filter_index])
# To implement gradient descent, we will need the gradient of this loss with respect to the model's input. To do this, we will use the
# `gradients` function packaged with the `backend` module of Keras:
# In[13]:
# The call to `gradients` returns a list of tensors (of size 1 in this case)
# hence we only keep the first element -- which is a tensor.
grads = K.gradients(loss, model.input)[0]
# A non-obvious trick to use for the gradient descent process to go smoothly is to normalize the gradient tensor, by dividing it by its L2
# norm (the square root of the average of the square of the values in the tensor). This ensures that the magnitude of the updates done to the
# input image is always within a same range.
# In[14]:
# We add 1e-5 before dividing so as to avoid accidentally dividing by 0.
grads /= (K.sqrt(K.mean(K.square(grads))) + 1e-5)
# Now we need a way to compute the value of the loss tensor and the gradient tensor, given an input image. We can define a Keras backend
# function to do this: `iterate` is a function that takes a Numpy tensor (as a list of tensors of size 1) and returns a list of two Numpy
# tensors: the loss value and the gradient value.
# In[15]:
iterate = K.function([model.input], [loss, grads])
# Let's test it:
import numpy as np
loss_value, grads_value = iterate([np.zeros((1, 150, 150, 3))])
# At this point we can define a Python loop to do stochastic gradient descent:
# In[16]:
# We start from a gray image with some noise
input_img_data = np.random.random((1, 150, 150, 3)) * 20 + 128.
# Run gradient ascent for 40 steps
step = 1. # this is the magnitude of each gradient update
for i in range(40):
# Compute the loss value and gradient value
loss_value, grads_value = iterate([input_img_data])
# Here we adjust the input image in the direction that maximizes the loss
input_img_data += grads_value * step
# The resulting image tensor will be a floating point tensor of shape `(1, 150, 150, 3)`, with values that may not be integer within `[0,
# 255]`. Hence we would need to post-process this tensor to turn it into a displayable image. We do it with the following straightforward
# utility function:
# In[17]:
def deprocess_image(x):
# normalize tensor: center on 0., ensure std is 0.1
x -= x.mean()
x /= (x.std() + 1e-5)
x *= 0.1
# clip to [0, 1]
x += 0.5
x = np.clip(x, 0, 1)
# convert to RGB array
x *= 255
x = np.clip(x, 0, 255).astype('uint8')
return x
# Now we have all the pieces, let's put them together into a Python function that takes as input a layer name and a filter index, and that
# returns a valid image tensor representing the pattern that maximizes the activation the specified filter:
# In[18]:
def generate_pattern(layer_name, filter_index, size=150):
# Build a loss function that maximizes the activation
# of the nth filter of the layer considered.
layer_output = model.get_layer(layer_name).output
loss = K.mean(layer_output[:, :, :, filter_index])
# Compute the gradient of the input picture wrt this loss
grads = K.gradients(loss, model.input)[0]
# Normalization trick: we normalize the gradient
grads /= (K.sqrt(K.mean(K.square(grads))) + 1e-5)
# This function returns the loss and grads given the input picture
iterate = K.function([model.input], [loss, grads])
# We start from a gray image with some noise
input_img_data = np.random.random((1, size, size, 3)) * 20 + 128.
# Run gradient ascent for 40 steps
step = 1.
for i in range(40):
loss_value, grads_value = iterate([input_img_data])
input_img_data += grads_value * step
img = input_img_data[0]
return deprocess_image(img)
# Let's try this:
# In[19]:
plt.imshow(generate_pattern('block3_conv1', 0))
plt.show()
# It seems that filter 0 in layer `block3_conv1` is responsive to a polka dot pattern.
#
# Now the fun part: we can start visualising every single filter in every layer. For simplicity, we will only look at the first 64 filters in
# each layer, and will only look at the first layer of each convolution block (block1_conv1, block2_conv1, block3_conv1, block4_conv1,
# block5_conv1). We will arrange the outputs on a 8x8 grid of 64x64 filter patterns, with some black margins between each filter pattern.
# In[22]:
for layer_name in ['block1_conv1', 'block2_conv1', 'block3_conv1', 'block4_conv1']:
size = 64
margin = 5
# This a empty (black) image where we will store our results.
results = np.zeros((8 * size + 7 * margin, 8 * size + 7 * margin, 3))
for i in range(8): # iterate over the rows of our results grid
for j in range(8): # iterate over the columns of our results grid
# Generate the pattern for filter `i + (j * 8)` in `layer_name`
filter_img = generate_pattern(layer_name, i + (j * 8), size=size)
# Put the result in the square `(i, j)` of the results grid
horizontal_start = i * size + i * margin
horizontal_end = horizontal_start + size
vertical_start = j * size + j * margin
vertical_end = vertical_start + size
results[horizontal_start: horizontal_end, vertical_start: vertical_end, :] = filter_img
# Display the results grid
plt.figure(figsize=(20, 20))
plt.imshow(results)
plt.show()
# These filter visualizations tell us a lot about how convnet layers see the world: each layer in a convnet simply learns a collection of
# filters such that their inputs can be expressed as a combination of the filters. This is similar to how the Fourier transform decomposes
# signals onto a bank of cosine functions. The filters in these convnet filter banks get increasingly complex and refined as we go higher-up
# in the model:
#
# * The filters from the first layer in the model (`block1_conv1`) encode simple directional edges and colors (or colored edges in some
# cases).
# * The filters from `block2_conv1` encode simple textures made from combinations of edges and colors.
# * The filters in higher-up layers start resembling textures found in natural images: feathers, eyes, leaves, etc.
# ## Visualizing heatmaps of class activation
#
# We will introduce one more visualization technique, one that is useful for understanding which parts of a given image led a convnet to its
# final classification decision. This is helpful for "debugging" the decision process of a convnet, in particular in case of a classification
# mistake. It also allows you to locate specific objects in an image.
#
# This general category of techniques is called "Class Activation Map" (CAM) visualization, and consists in producing heatmaps of "class
# activation" over input images. A "class activation" heatmap is a 2D grid of scores associated with an specific output class, computed for
# every location in any input image, indicating how important each location is with respect to the class considered. For instance, given a
# image fed into one of our "cat vs. dog" convnet, Class Activation Map visualization allows us to generate a heatmap for the class "cat",
# indicating how cat-like different parts of the image are, and likewise for the class "dog", indicating how dog-like differents parts of the
# image are.
#
# The specific implementation we will use is the one described in [Grad-CAM: Why did you say that? Visual Explanations from Deep Networks via
# Gradient-based Localization](https://arxiv.org/abs/1610.02391). It is very simple: it consists in taking the output feature map of a
# convolution layer given an input image, and weighing every channel in that feature map by the gradient of the class with respect to the
# channel. Intuitively, one way to understand this trick is that we are weighting a spatial map of "how intensely the input image activates
# different channels" by "how important each channel is with regard to the class", resulting in a spatial map of "how intensely the input
# image activates the class".
#
# We will demonstrate this technique using the pre-trained VGG16 network again:
# In[24]:
from keras.applications.vgg16 import VGG16
K.clear_session()
# Note that we are including the densely-connected classifier on top;
# all previous times, we were discarding it.
model = VGG16(weights='imagenet')
# Let's consider the following image of two African elephants, possible a mother and its cub, strolling in the savanna (under a Creative
# Commons license):
#
# 
# Let's convert this image into something the VGG16 model can read: the model was trained on images of size 224x244, preprocessed according
# to a few rules that are packaged in the utility function `keras.applications.vgg16.preprocess_input`. So we need to load the image, resize
# it to 224x224, convert it to a Numpy float32 tensor, and apply these pre-processing rules.
# In[27]:
from keras.preprocessing import image
from keras.applications.vgg16 import preprocess_input, decode_predictions
import numpy as np
# The local path to our target image
img_path = '/Users/fchollet/Downloads/creative_commons_elephant.jpg'
# `img` is a PIL image of size 224x224
img = image.load_img(img_path, target_size=(224, 224))
# `x` is a float32 Numpy array of shape (224, 224, 3)
x = image.img_to_array(img)
# We add a dimension to transform our array into a "batch"
# of size (1, 224, 224, 3)
x = np.expand_dims(x, axis=0)
# Finally we preprocess the batch
# (this does channel-wise color normalization)
x = preprocess_input(x)
# In[29]:
preds = model.predict(x)
print('Predicted:', decode_predictions(preds, top=3)[0])
#
# The top-3 classes predicted for this image are:
#
# * African elephant (with 92.5% probability)
# * Tusker (with 7% probability)
# * Indian elephant (with 0.4% probability)
#
# Thus our network has recognized our image as containing an undetermined quantity of African elephants. The entry in the prediction vector
# that was maximally activated is the one corresponding to the "African elephant" class, at index 386:
# In[30]:
np.argmax(preds[0])
# To visualize which parts of our image were the most "African elephant"-like, let's set up the Grad-CAM process:
# In[31]:
# This is the "african elephant" entry in the prediction vector
african_elephant_output = model.output[:, 386]
# The is the output feature map of the `block5_conv3` layer,
# the last convolutional layer in VGG16
last_conv_layer = model.get_layer('block5_conv3')
# This is the gradient of the "african elephant" class with regard to
# the output feature map of `block5_conv3`
grads = K.gradients(african_elephant_output, last_conv_layer.output)[0]
# This is a vector of shape (512,), where each entry
# is the mean intensity of the gradient over a specific feature map channel
pooled_grads = K.mean(grads, axis=(0, 1, 2))
# This function allows us to access the values of the quantities we just defined:
# `pooled_grads` and the output feature map of `block5_conv3`,
# given a sample image
iterate = K.function([model.input], [pooled_grads, last_conv_layer.output[0]])
# These are the values of these two quantities, as Numpy arrays,
# given our sample image of two elephants
pooled_grads_value, conv_layer_output_value = iterate([x])
# We multiply each channel in the feature map array
# by "how important this channel is" with regard to the elephant class
for i in range(512):
conv_layer_output_value[:, :, i] *= pooled_grads_value[i]
# The channel-wise mean of the resulting feature map
# is our heatmap of class activation
heatmap = np.mean(conv_layer_output_value, axis=-1)
# For visualization purpose, we will also normalize the heatmap between 0 and 1:
# In[32]:
heatmap = np.maximum(heatmap, 0)
heatmap /= np.max(heatmap)
plt.matshow(heatmap)
plt.show()
# Finally, we will use OpenCV to generate an image that superimposes the original image with the heatmap we just obtained:
# In[ ]:
import cv2
# We use cv2 to load the original image
img = cv2.imread(img_path)
# We resize the heatmap to have the same size as the original image
heatmap = cv2.resize(heatmap, (img.shape[1], img.shape[0]))
# We convert the heatmap to RGB
heatmap = np.uint8(255 * heatmap)
# We apply the heatmap to the original image
heatmap = cv2.applyColorMap(heatmap, cv2.COLORMAP_JET)
# 0.4 here is a heatmap intensity factor
superimposed_img = heatmap * 0.4 + img
# Save the image to disk
cv2.imwrite('/Users/fchollet/Downloads/elephant_cam.jpg', superimposed_img)
测试图片:
结果:
欢迎关注我的公众号:
编程技术与生活(ID:hw_cchang)
![]()