IJCAI‘19 Semi-supervised User Profiling with Heterogeneous Graph Attention Networks阅读笔记
IJCAI19–Semi-supervised User Profiling with Heterogeneous Graph Attention Networks
引言
当前用户画像任务大多视为分类任务,利用文本或行为信息分类用户的个性化画像,如性别、年龄等,在这之中,将每一个用户看作是个体实例,但这存在两个问题:
- 只有一种类型的信息被用于推断用户画像,并且其他类型的数据无法自然地集成。极少地研究触及多类型用户画像问题。需要设计手工制作地特征或混合方法。
- 仅利用到了个体自己的特征,一些相同特征则被忽视掉,例如共同点击、共同购买,社交网络中用户的关系也可看做一种半监督信号用于提升用户画像构建。
本文贡献:
- 提出了异构图中半监督的用户画像构建方法,为开发多种类型数据集成的解决方案提供了思路。
- 我们开发了一个异构的图注意力网络框架HGAT,充分利用图结构和节点特性,从有限的标记数据中学习用户画像。
相关研究
用户画像
逻辑回归、支持向量机、梯度提升决策树对用户性别等信息进行预测
利用深度神经网络和注意力机制等进行预测,但是需要手工设计特征或混合方法。
图注意力网络
GAT是GCN的扩展,使用一个遮盖的自组伊利层,能够分配给不同邻居不同权重。
问题形式化T
异构图
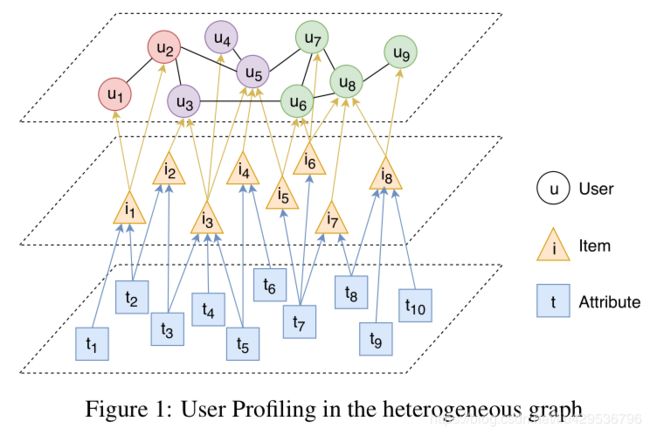
如图1,异构图G(V,E)中V包含用户、项目、属性,边包含用户间的关系 E u u E_{uu} Euu,用户项目的交互 E u i E_{ui} Eui,以及项目具有的属性 E i a E_{ia} Eia。
例如在电商场景中,item就是产品,属性可能就是商品标题中包含的词,每一个产品包含一些属性(词),每一名用户可能购买了一些产品。 E u u E_{uu} Euu表示用户有共同购买或是共同点击。
异构图中的子图
根据边的不同可以分为三个子图,即用户-用户子图、用户-项目子图、属性-项目子图
半监督的用户画像
一个用户画像问题是推断用户性别和年龄标签。
论文的目标是使用一些用户的标签和大量的异构图中的非监督信息,例如用户、项目、属性间的交互。
定义3.1半监督的用户画像问题
半监督用户画像旨在基于一些用户的监督标签和大量的异构图中的非监督信息推断用户标签。
异构图注意力网络(HGAT)
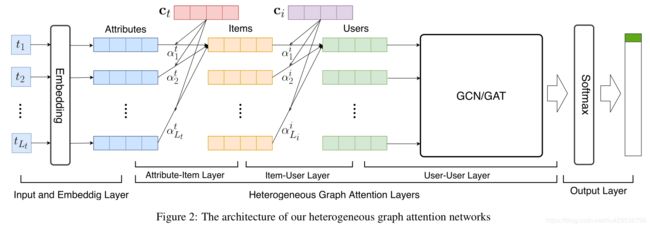
输入层和嵌入层
输入层是异构图中节点和边的信息。
属性嵌入使用Fast-Text利用整个项目标题语料库学习词嵌入。这些嵌入向量被看作属性的低维表示。
异构图注意力层
异构图表示学习的两个问题:
-
如何更新节点嵌入向量
-
信息如何在异构图中传播
对于问题一,使用3异构图注意力操作进行嵌入向量更新。对于问题二,提出源路径感知的图传播定义异构图中信息传播方法
异构图注意力操作
异构图注意力操作基于邻居节点信息更新节点的嵌入向量。将节点嵌入向量矩阵从 H ∈ R ∣ V ∣ × F \mathbf{H} \in \mathbb{R}^{|V| \times F} H∈R∣V∣×F转换为 H ′ ∈ R ∣ V ∣ × F ′ \mathbf{H}^{\prime} \in \mathbb{R}^{|V| \times F^{\prime}} H′∈R∣V∣×F′。这些操作的不同点在于计算方式。
论文中使用了三种异构图注意力操作: Vanilla Attention Operation,图卷积操作和图注意力操作
Vanilla Attention Operation
给定一个节点 i i i和他的邻居 N i \mathcal{N}_{i} Ni,它的新嵌入向量 h i ′ \mathbf{h}_{i}^{\prime} hi′被如下步骤计算:
e i j = c T tanh ( W h j + b ) α i j = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) h i ′ = ∑ j ∈ N i α i j h j \begin{array}{l} e_{i j}=\mathbf{c}^{T} \tanh \left(\mathbf{W h}_{j}+\mathbf{b}\right) \\ \alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)} \\ \mathbf{h}_{i}^{\prime}=\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{h}_{j} \end{array} eij=cTtanh(Whj+b)αij=∑k∈Niexp(eik)exp(eij)hi′=∑j∈Niαijhj {(1)}
其中 c ∈ R F ′ \mathbf{c} \in \mathbb{R}^{F^{\prime}} c∈RF′表示上下文向量,权重矩阵 W ∈ R F ′ × F \mathbf{W} \in \mathbb{R}^{F^{\prime} \times F} W∈RF′×F和偏置向量 b ∈ R F ′ \mathbf{b} \in \mathbb{R}^{F^{\prime}} b∈RF′是参数。这些参数用于计算注意力分数 α i j \alpha_{i j} αij,表示邻居节点 j j j和节点 i i i的重要性。
图卷积操作
A ^ = D ~ − 1 / 2 A ~ D ~ − 1 / 2 H ′ = σ ( A ^ H W T ) \begin{array}{l} \hat{\mathbf{A}}=\widetilde{\mathbf{D}}^{-1 / 2} \tilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-1 / 2} \\ \mathbf{H}^{\prime}=\sigma\left(\hat{\mathbf{A}} \mathbf{H} \mathbf{W}^{T}\right) \end{array} A^=D −1/2A~D −1/2H′=σ(A^HWT)
其中 A ~ = A + I ∣ V ∣ \tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}_{|V|} A~=A+I∣V∣是邻接矩阵加上自循环(相应的单位矩阵), D ~ ∈ \widetilde{\mathbf{D}} \in D ∈ R ∣ V ∣ × ∣ V ∣ \mathbb{R}^{|V| \times|V|} R∣V∣×∣V∣是矩阵 A ~ \tilde{\mathbf{A}} A~的都矩阵, W ∈ R F ′ × F \mathbf{W} \in \mathbb{R}^{F^{\prime} \times F} W∈RF′×F表示权重矩阵,其中 σ \sigma σ表示激活函数。
图注意力操作
图注意力操作利用被用于图注意力网络的多端图注意力操作。首先,它基于一个共享的注意机制 a t t att att计算节点间的注意力分数: R F ′ × R F ′ → R \mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R} RF′×RF′→R。节点 i i i的邻居表示为 N i \mathcal{N_{i}} Ni对于每一个 j ∈ N i j \in \mathcal{N}_{i} j∈Ni,节点 i i i和节点 j j j的注意力系数为 e i j e_{ij} eij。利用softmax函数将分数进行标准化:
e i j = a t t ( W h i , W h j ) α i j = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) \begin{array}{l} e_{i j}=a t t\left(\mathbf{W} \mathbf{h}_{i}, \mathbf{W h}_{j}\right) \\ \alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)} \end{array} eij=att(Whi,Whj)αij=∑k∈Niexp(eik)exp(eij)
其中注意力机制 a t t att att是单层前馈神经网络,参数化 W ∈ R F ′ × F \mathbf{W} \in \mathbb{R}^{F^{\prime} \times F} W∈RF′×F和 a ∈ R 2 F ′ \mathbf{a} \in \mathbb{R}^{2 F^{\prime}} a∈R2F′,并使用LeakyReLU映射到非线性空间:
att ( W h i , W h j ) = Leaky Re L U ( a T [ W h i ∣ ∣ W h j ] ) \operatorname{att}\left(\mathbf{W} \mathbf{h}_{i}, \mathbf{W} \mathbf{h}_{j}\right)=\text {Leaky} \operatorname{Re} L U\left(\mathbf{a}^{T}\left[\mathbf{W} \mathbf{h}_{i}|| \mathbf{W} \mathbf{h}_{j}\right]\right) att(Whi,Whj)=LeakyReLU(aT[Whi∣∣Whj])
其中 ∣ ∣ || ∣∣表示两个向量的串联。第二,节点新的嵌入向量 h i ′ \mathbf{h}_{i}^{\prime} hi′由加和它邻居的特征并通过注意力分数加权得到:
h i ′ = σ ( ∑ j ∈ N i α i j W h j ) \mathbf{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \mathbf{h}_{j}\right) hi′=σ⎝⎛j∈Ni∑αijWhj⎠⎞
多端注意力记住被用于增强表示能力。具体来说,就是由 K K K个独立的注意力机制使用上面的灯饰,之后得到 K K K个结果 h i ′ ( 1 ) , h i ′ ( 2 ) , … , h i ′ ( K ) \mathbf{h}_{i}^{\prime(1)}, \mathbf{h}_{i}^{\prime(2)}, \ldots, \mathbf{h}_{i}^{\prime(K)} hi′(1),hi′(2),…,hi′(K)聚合为结果:
h i ′ = σ ( agg ( h i ′ ( 1 ) , h i ′ ( 2 ) , … , h i ′ ( K ) ) ) \mathbf{h}_{i}^{\prime}=\sigma\left(\operatorname{agg}\left(\mathbf{h}_{i}^{\prime(1)}, \mathbf{h}_{i}^{\prime(2)}, \ldots, \mathbf{h}_{i}^{\prime(K)}\right)\right) hi′=σ(agg(hi′(1),hi′(2),…,hi′(K)))
聚合函数 a g g agg agg可以是串联或者平均。特别地,如果我们在最后一层使用多端注意力机制,会采用平均。否则使用串联操作。
源路径感知图注意力传播
属性项目层
属性项目层传播属性到项目的信息。本层使用Vanilla Attention Operation传播属性项目子图并且借助属性嵌入向量和项目和属性的边学习项目嵌入向量。
项目用户层
本层传播项目到用户的信息,也是用Vanilla Attention Operation传播项目-用户子图信息并且借助项目嵌入向量和用户项目间的边歇息用户嵌入向量。
用户用户层
本层传播用户到用户的信息。本层应用图卷积操作或是图注意力操作传播用户用户子图信息并且学习用户嵌入向量。最终,模型会将所有相关用户映射到矩阵 H u ∈ R ∣ U ∣ × F Y \mathbf{H}_{u} \in \mathbb{R}^{|U| \times F_{Y}} Hu∈R∣U∣×FY其中 F Y F_{Y} FY是用户嵌入向量的维度,将会被设置为与用户画像任务标签的数量相等。
输出层
输出层基于学得的用户嵌入向量预测用户标签。对于用户画像任务中的 F Y F_{Y} FY是类型数量(例如用户标签),对用户嵌入向量矩阵 H u \mathbf{H}_{u} Hu使用行级别的softmax函数并获得 Z ∈ R ∣ U ∣ × F Y \mathbf{Z} \in\mathbb{R}^{|U| \times F_{Y}} Z∈R∣U∣×FY,为预测的用户标签分布。
模型训练
交叉熵损失函数
L = − ∑ u ∈ U L ∑ f = 1 F Y Y u f log Z u f \mathcal{L}=-\sum_{u \in U_{L}} \sum_{f=1}^{F_{Y}} Y_{u f} \log Z_{u f} L=−u∈UL∑f=1∑FYYuflogZuf
其中 U L U_{L} UL是存在标签的用户集合, Y \mathbf{Y} Y和 Z \mathbf{Z} Z分别是真实地标签值和预测的用户标签概率分布。
个人感悟
论文利用三种不同的注意力机制(Vanilla Attention、GCN、Graph Attention Operation)分别应用于计算每个实体下各个属性(标题中的词)的嵌入向量权重和用户交互项目和用户权重以及用户之间的嵌入向量相似度权重。这种方法能够很好地对属性和项目进行区分,因为论文所描述的异构图中各个子图的边是相同含义的,所以需要加入注意力机制进行区分。
论文提出的模型和微软亚洲研究院在WWW‘19上提出的KGCN模型都表明:利用图学习用户或项目的嵌入向量一定要加入一个注意力机制的操作,对边权重加以区分。