高斯牛顿法的曲线拟合实验
最小二乘法:又称最小平方法,是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。完整代码可见
https://github.com/YCJin9/sparse_BA
高斯牛顿法是最优化算法当中最简单的一种,这会便于我们去实现,但同时高斯牛顿法有着他本身的问题,这会在本篇博客的最后进行展示。
高博十四讲中第六讲提供了用Ceres和g2o实现曲线拟合的程序,这篇博客是要手写一个高斯牛顿法实现这个拟合曲线的程序,同时最小二乘法的理论基础也可以在第六讲找到,相信大家也都了解。
1、构建最小二乘问题:
假设有一条满足一下方程的曲线:
![]()
其中a, b, c为曲线参数, 为高斯噪声。有N个关于x, y的观测数据点,根据这些数据求出曲线参数。那么,可以求解下面的最小二乘问题以估计曲线参数:
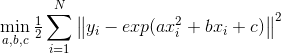
先根据模型生成N个关于x, y的真值,然后在真值中添加高斯分布的噪声产生观测数据。
为方便验证,我们使用的观测数据产生方式与高博十四讲中第六讲Ceres和g2o相同,使用OpenCV的随机数产生器。
double a=1.0, b=2.0, c=1.0; // 真实参数值
int N=100; // 数据点
double w_sigma=1.0; // 噪声Sigma值
cv::RNG rng; // OpenCV随机数产生器
double ae=2.0, be=-1.0, ce=5.0; // abc参数的估计值
vector x_data, y_data; // 数据
cout<<"generating data…… "< 2、实现高斯牛顿迭代
高斯牛顿法的主要步骤是在每一次迭代中用作为Hessian矩阵的近似,求解增量方程。
单个数据点的误差
![]()
雅克比矩阵
![]()
// 开始Gauss-Newton迭代
int iterations = 100; // 迭代次数
double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost
for (int iter = 0; iter < iterations; iter++) {
Matrix3d H = Matrix3d::Zero(); // Hessian = J^T J
Vector3d b = Vector3d::Zero(); // bias
cost = 0;
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据点
double error = 0; // 第i个数据点的计算误差
error = yi-exp(ae * xi * xi + be * xi + ce);
Vector3d J; // 雅可比矩阵
J[0] = -xi*xi*exp(ae*xi*xi+be*xi+ce);
J[1] = -xi*exp(ae*xi*xi+be*xi+ce);
J[2] = -exp(ae*xi*xi+be*xi+ce);
H += J * J.transpose();
b += -error * J;
cost += error * error;
}
Vector3d dx;
dx = H.inverse()*b;
//dx = H.colPivHouseholderQr().solve(b); //QR分解,可加快求解速度
//dx = H.ldlt().solve(b); //ldlt分解,可加快求解速度
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost > lastCost) {
// 误差增长了,说明近似的不够好
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// 更新abc估计值
ae += dx[0];
be += dx[1];
ce += dx[2];
lastCost = cost;
cout << "total cost: " << cost << endl;
}
// 开始Gauss-Newton迭代
int iterations = 100; // 迭代次数
double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost
for (int iter = 0; iter < iterations; iter++) {
Matrix3d H = Matrix3d::Zero(); // Hessian = J^T J
Vector3d b = Vector3d::Zero(); // bias
cost = 0;
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据点
double error = 0; // 第i个数据点的计算误差
error = yi-exp(ae * xi * xi + be * xi + ce);
Vector3d J; // 雅可比矩阵
J[0] = -xi*xi*exp(ae*xi*xi+be*xi+ce);
J[1] = -xi*exp(ae*xi*xi+be*xi+ce);
J[2] = -exp(ae*xi*xi+be*xi+ce);
H += J * J.transpose();
b += -error * J;
cost += error * error;
}
Vector3d dx;
dx = H.inverse()*b;
//dx = H.colPivHouseholderQr().solve(b); //QR分解,可加快求解速度
//dx = H.ldlt().solve(b); //ldlt分解,可加快求解速度
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost > lastCost) {
// 误差增长了,说明近似的不够好
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// 更新abc估计值
ae += dx[0];
be += dx[1];
ce += dx[2];
lastCost = cost;
cout << "total cost: " << cost << endl;
}
cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
3、程序运行结果
最后输出的结果应该与十四讲中的结果基本一致,即 a = 0.890912, b = 2.1719, c = 0.943629
4、高斯牛顿法缺点展示
在程序中我们改变abc的参数估计初值,可能会导致结果不收敛,例如:我们更改abc初值为0, 0, 0,程序运行结果如下:

迭代结果不收敛的原因:一是因为高斯牛顿法使用作为Hessian矩阵的近似,原则上H矩阵是可逆且正定的,但实际数据计算得到的可能出现为奇异矩阵或者病态的情况,此时增量的稳定性较差,导致算法不收敛;另一方面,高斯牛顿法将f(x)一阶泰勒展开进行近似,即:,当求出的步长 太大时也会导致近似不够准确使得结果不收敛。
当然我们并不能因为这些问题就放弃高斯牛顿法的学习,高斯牛顿法是最简单的非线性优化方法,同时也是很多优化算法的基础,很多算法都可以看作是高斯牛顿法的变种,借助了高斯牛顿法的思想改进修正其缺点。
5.整体代码
//
// on 2017/12/15.
//
#include
#include
#include
#include
using namespace std;
using namespace Eigen;
int main(int argc, char **argv) {
double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值
int N = 100; // 数据点
double w_sigma = 1.0; // 噪声Sigma值
cv::RNG rng; // OpenCV随机数产生器
vector x_data, y_data; // 生成数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma));
}
// 开始Gauss-Newton迭代
int iterations = 100; // 迭代次数
double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost
for (int iter = 0; iter < iterations; iter++) {
Matrix3d H = Matrix3d::Zero(); // Hessian = J^T J in Gauss-Newton
Vector3d b = Vector3d::Zero(); // bias
cost = 0;
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据
// start your code here
double error = 0; // 第i个数据点的计算误差
error = yi-exp(ae*xi*xi+be*xi+ce); // 填写计算error的表达式
Vector3d J; // 雅可比矩阵
J[0] = -xi*xi*exp(ae*xi*xi+be*xi+ce); // de/da
J[1] = -xi*exp(ae*xi*xi+be*xi+ce); // de/db
J[2] = -exp(ae*xi*xi+be*xi+ce); // de/dc
H += J * J.transpose(); // GN近似的H
b += -error * J;
// end your code here
cost += error * error;
}
// 求解线性方程 Hx=b,建议用ldlt
// start your code here
Vector3d dx;
dx=H.inverse()*b;
//dx = H.colPivHouseholderQr().solve(b); //QR分解,可加快求解速度
//dx = H.ldlt().solve(b); //ldlt分解,可加快求解速度
// end your code here
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost > lastCost) {
// 误差增长了,说明近似的不够好
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// 更新abc估计值
ae += dx[0];
be += dx[1];
ce += dx[2];
lastCost = cost;
cout << "total cost: " << cost << endl;
}
cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
return 0;
}