矩阵快速幂+费马小定理---牛客寒假集训营1-u's的影响力+M斐波那契数列 HDU - 4549
矩阵快速幂+费马小定理—牛客寒假集训营1-u’s的影响力+M斐波那契数列 HDU - 4549
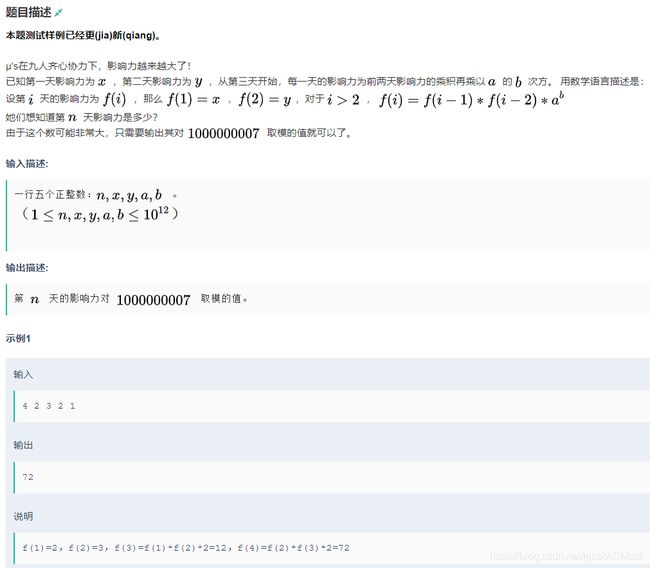
给 定 表 达 式 f ( i ) = f ( i − 1 ) ∗ f ( i − 2 ) ∗ a b ( i > 2 ) , 现 输 入 n 、 f ( 1 ) 、 f ( 2 ) 、 a 、 b , 求 f ( n ) 给定表达式f(i)=f(i-1)*f(i-2)*a^b \ (i>2),现输入n、f(1)、f(2)、a、b,求f(n) 给定表达式f(i)=f(i−1)∗f(i−2)∗ab (i>2),现输入n、f(1)、f(2)、a、b,求f(n)
题解:
矩 阵 快 速 幂 + 整 数 快 速 幂 + 费 马 小 定 理 , 算 法 时 间 复 杂 度 O ( l o g n ) 矩阵快速幂+整数快速幂+费马小定理,算法时间复杂度O(logn) 矩阵快速幂+整数快速幂+费马小定理,算法时间复杂度O(logn)
整 个 算 法 分 为 两 个 部 分 , 整个算法分为两个部分, 整个算法分为两个部分,
一 、 矩 阵 快 速 幂 计 算 指 数 。 一、矩阵快速幂计算指数。 一、矩阵快速幂计算指数。
二 、 整 数 快 速 幂 + 费 马 小 定 理 计 算 最 终 结 果 。 二、整数快速幂+费马小定理计算最终结果。 二、整数快速幂+费马小定理计算最终结果。
先 写 几 项 找 找 递 推 的 规 律 : 先写几项找找递推的规律: 先写几项找找递推的规律:
f ( 1 ) = x 1 y 0 a 0 , f(1)=x^1y^0a^0, f(1)=x1y0a0,
f ( 2 ) = x 0 y 1 a 0 , f(2)=x^0y^1a^0, f(2)=x0y1a0,
f ( 3 ) = x 1 y 1 a b , f(3)=x^1y^1a^b, f(3)=x1y1ab,
f ( 4 ) = x 1 y 2 a 2 b , f(4)=x^1y^2a^{2b}, f(4)=x1y2a2b,
f ( 5 ) = x 2 y 3 a 4 b , f(5)=x^2y^3a^{4b}, f(5)=x2y3a4b,
f ( 6 ) = x 3 y 5 a 7 b , f(6)=x^3y^5a^{7b}, f(6)=x3y5a7b,
. . . . . . ...... ......
我 们 发 现 , 从 第 三 项 起 , 每 一 项 指 数 都 是 前 两 项 对 应 的 指 数 之 和 我们发现,从第三项起,每一项指数都是前两项对应的指数之和 我们发现,从第三项起,每一项指数都是前两项对应的指数之和
因 为 原 递 推 式 是 前 两 项 之 积 , 那 么 转 化 到 指 数 上 来 就 是 指 数 之 和 因为原递推式是前两项之积,那么转化到指数上来就是指数之和 因为原递推式是前两项之积,那么转化到指数上来就是指数之和
设 斐 波 那 契 数 列 F ( n ) = F ( n − 1 ) + F ( n − 2 ) ( n > = 3 ) , 设斐波那契数列F(n)=F(n-1)+F(n-2) (n>=3), 设斐波那契数列F(n)=F(n−1)+F(n−2)(n>=3),
①、
对 x 和 y 而 言 , 它 们 在 f ( 1 ) 和 f ( 2 ) 中 的 指 数 分 别 是 { 1 , 0 } 和 { 0 , 1 } , 对x和y而言,它们在f(1)和f(2)中的指数分别是\{1,0\}和\{0,1\}, 对x和y而言,它们在f(1)和f(2)中的指数分别是{1,0}和{0,1},
那 么 在 第 n 项 f ( n ) 中 , x 和 y 的 指 数 分 别 对 应 为 F x ( n ) 和 F y ( n ) 那么在第n项f(n)中,x和y的指数分别对应为F_x(n)和F_y(n) 那么在第n项f(n)中,x和y的指数分别对应为Fx(n)和Fy(n)
F x ( 1 ) = 1 , F x ( 2 ) = 0 , F x ( n ) = F x ( n − 1 ) + F x ( n − 2 ) ( n > = 3 ) F_x(1)=1,F_x(2)=0,F_x(n)=F_x(n-1)+F_x(n-2) (n>=3) Fx(1)=1,Fx(2)=0,Fx(n)=Fx(n−1)+Fx(n−2)(n>=3)
F y ( 1 ) = 0 , F y ( 2 ) = 1 , F y ( n ) = F y ( n − 1 ) + F y ( n − 2 ) ( n > = 3 ) F_y(1)=0,F_y(2)=1,F_y(n)=F_y(n-1)+F_y(n-2) (n>=3) Fy(1)=0,Fy(2)=1,Fy(n)=Fy(n−1)+Fy(n−2)(n>=3)
斐 波 那 契 数 列 的 变 换 矩 阵 是 : 斐波那契数列的变换矩阵是: 斐波那契数列的变换矩阵是:
M = ∣ 0 1 1 1 ∣ , 则 ∣ 0 1 1 1 ∣ ⋅ ∣ f ( i − 2 ) f ( i − 1 ) ∣ = ∣ f ( i − 1 ) f ( i − 1 ) + f ( i − 2 ) ∣ = ∣ f ( i − 1 ) f ( i ) ∣ M=\begin{vmatrix} 0 & 1 \\ 1 & 1 \\ \end{vmatrix},则\begin{vmatrix} 0 & 1 \\ 1 & 1 \\ \end{vmatrix}·\begin{vmatrix} f(i-2) \\ f(i-1) \end{vmatrix}=\begin{vmatrix} f(i-1) \\f(i-1)+ f(i-2) \end{vmatrix}=\begin{vmatrix} f(i-1) \\ f(i) \end{vmatrix} M=∣∣∣∣0111∣∣∣∣,则∣∣∣∣0111∣∣∣∣⋅∣∣∣∣f(i−2)f(i−1)∣∣∣∣=∣∣∣∣f(i−1)f(i−1)+f(i−2)∣∣∣∣=∣∣∣∣f(i−1)f(i)∣∣∣∣
②、
对 a 而 言 , 每 一 项 的 指 数 都 是 前 两 项 指 数 之 和 再 加 上 1 , 对a而言,每一项的指数都是前两项指数之和再加上1, 对a而言,每一项的指数都是前两项指数之和再加上1,
F a ( 1 ) = 0 , F a ( 2 ) = 0 , F x ( n ) = F a ( n − 1 ) + F a ( n − 2 ) + 1 ( n > = 3 ) F_a(1)=0,F_a(2)=0,F_x(n)=F_a(n-1)+F_a(n-2)+1 (n>=3) Fa(1)=0,Fa(2)=0,Fx(n)=Fa(n−1)+Fa(n−2)+1(n>=3)
于 是 可 以 设 关 系 矩 阵 : 于是可以设关系矩阵: 于是可以设关系矩阵:
A = ∣ f ( i − 2 ) f ( i − 1 ) 1 ∣ A=\begin{vmatrix} f(i-2) \\ f(i-1)\\1 \end{vmatrix} A=∣∣∣∣∣∣f(i−2)f(i−1)1∣∣∣∣∣∣
进 而 得 到 矩 阵 a 的 指 数 的 变 换 矩 阵 : 进而得到矩阵a的指数的变换矩阵: 进而得到矩阵a的指数的变换矩阵:
M a = ∣ 0 1 0 1 1 1 0 0 1 ∣ , 那 么 ∣ 0 1 0 1 1 1 0 0 1 ∣ ⋅ ∣ f ( i − 2 ) f ( i − 1 ) 1 ∣ = ∣ f ( i − 1 ) f ( i − 2 ) + f ( i − 1 ) + 1 1 ∣ = ∣ f ( i − 1 ) f ( i ) 1 ∣ Ma=\begin{vmatrix} 0 & 1 & 0 \\ 1 & 1 & 1\\0 & 0 & 1 \end{vmatrix},那么\begin{vmatrix} 0 & 1 & 0 \\ 1 & 1 & 1\\0 & 0 & 1 \end{vmatrix}·\begin{vmatrix} f(i-2) \\ f(i-1)\\1 \end{vmatrix}=\begin{vmatrix} f(i-1) \\ f(i-2)+f(i-1)+1\\1 \end{vmatrix}=\begin{vmatrix} f(i-1) \\ f(i)\\1 \end{vmatrix} Ma=∣∣∣∣∣∣010110011∣∣∣∣∣∣,那么∣∣∣∣∣∣010110011∣∣∣∣∣∣⋅∣∣∣∣∣∣f(i−2)f(i−1)1∣∣∣∣∣∣=∣∣∣∣∣∣f(i−1)f(i−2)+f(i−1)+11∣∣∣∣∣∣=∣∣∣∣∣∣f(i−1)f(i)1∣∣∣∣∣∣
③、
到 这 里 , f ( n ) = x F x ( n ) ⋅ y F y ( n ) ⋅ a F a ( n ) ⋅ b , 就 可 以 计 算 出 来 了 。 到这里,f(n)=x^{F_x(n)}·y^{F_y(n)}·a^{F_a(n)·b} ,就可以计算出来了。 到这里,f(n)=xFx(n)⋅yFy(n)⋅aFa(n)⋅b,就可以计算出来了。
但 是 考 虑 到 取 模 问 题 , m o d = 1 e 9 + 7 是 质 数 , 但是考虑到取模问题,mod=1e9+7是质数, 但是考虑到取模问题,mod=1e9+7是质数,
根 据 费 马 小 定 理 , 若 p 与 q 互 质 , 则 p q − 1 ≡ 1 ( m o d q ) 根据费马小定理,若p与q互质,则p^{q-1}≡1(mod\ q) 根据费马小定理,若p与q互质,则pq−1≡1(mod q)
若 p 与 1 e 9 + 7 互 质 ( a 不 是 1 e 9 + 7 的 倍 数 ) , 则 p 1 e 9 + 6 ≡ 1 ( m o d 1 e 9 + 7 ) 若p与1e9+7互质(a不是1e9+7的倍数),则\ p^{1e9+6}≡1(mod\ 1e9+7) 若p与1e9+7互质(a不是1e9+7的倍数),则 p1e9+6≡1(mod 1e9+7)
因 此 在 计 算 快 速 幂 时 , 可 将 指 数 对 m o d − 1 = 1 e 9 + 6 取 模 来 优 化 计 算 因此在计算快速幂时,可将指数对\ mod-1=1e9+6\ 取模来优化计算 因此在计算快速幂时,可将指数对 mod−1=1e9+6 取模来优化计算
代码:
#include///—HDU - 4549
HDU有一道类似但是更简单的一道题:M斐波那契数列 HDU - 4549
记下来做个对比
题目:
M斐波那契数列F[n]是一种整数数列,它的定义如下:
F[0] = a
F[1] = b
F[n] = F[n-1] * F[n-2] ( n > 1 )
现在给出a, b, n,你能求出F[n]的值吗?
Input
输入包含多组测试数据;
每组数据占一行,包含3个整数a, b, n( 0 <= a, b, n <= 10^9 )
Output
对每组测试数据请输出一个整数F[n],由于F[n]可能很大,你只需输出F[n]对1000000007取模后的值即可,每组数据输出一行。
Sample Input
0 1 0
6 10 2
Sample Output
0
60
题解:
牛客的题应该就是改编了这题,同样的模板,唯一的区别就是HDU这道题是从第0项开始,修改输入即可。
代码:
#include