cv论文笔记：Semi-Supervised Deep Learning for Monocular Depth Map Prediction（无监督深度预测系列3：半监督方法）

一、基本信息

标题：Semi-Supervised Deep Learning for Monocular Depth Map Prediction
时间：2017
引用格式：Kuznietsov Y, Stuckler J, Leibe B. Semi-supervised deep learning for monocular depth map prediction[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 6647-6655.

二、研究背景

监督学习：需要大量标记数据，激光雷达RGBD等获取的数据存在噪声且稀疏，激光与照相机的投影中心不重合
无监督学习：对应没有纹理的地方，预测不了

总结一下深度预测发展：

• Saxena et al. 第一个基于监督学习方法，使用MRF，手动提取特征
• Eigen et al.使用CNN，由粗到细的多层网络。笔记
• Li et al.使用CNN结合CRFs超像素分割
• Liu et al.端到端训练一元势和成对势的CNN特征，连续深度和高斯假设？？
• Laina et al.使用ResNet构建深度卷积，得到预测密度更大
• 此后，图像的深度转移的思想[或者将深度图预测与语义分割相结合
• Garg et al. FCN FlowNet 使用光测误差。（利用一阶泰勒近似将损失线性化，因此需要从粗到细的训练？？）
• Xie et al. 视差方法，最小化像素级重建误差。
• Godard et al.也是视差方法，最小重建误差，但是使用左右约束。笔记

三、创新点

本文提出使用监督和非监督结合的方法。一个训练配对图需要2张深度图（LiDAR获得），2张RGB图。

令CNN预测的深度倒数$\rho (\mathbf{x})$和激光雷达得到的深度$Z(\mathbf{x})$对应关系：
$$\rho (\mathbf{x}{)}^{-1}\stackrel{!}{=}Z(\mathbf{x})$$

图像减去视差$fb\rho (\mathbf{x})$：
$$\omega (\mathbf{x},\rho (\mathbf{x})):=\mathbf{x}-fb\rho (\mathbf{x})$$

令左图$I_1$等于右图$I_2$-视差：
$$I_1(\mathbf{x})\stackrel{!}{=}{I}_2(\omega (\mathbf{x},\rho (\mathbf{x})))$$

结合左右图像：
$$\begin{array}{c}{I}_{\text{left}}(\mathbf{x})\stackrel{!}{=}{I}_{\text{right}}(\omega (\mathbf{x},\rho (\mathbf{x})))\\ I_{\text{right}}(\mathbf{x})\stackrel{!}{=}{I}_{\text{left}}(\omega (\mathbf{x},-\rho (\mathbf{x})))\end{array}$$

损失函数

Supervised loss.

$$\begin{array}{rl}{\mathcal{L}}_{\mathbf{\theta }}^S=\sum _{\mathbf{x}\in {\Omega }_{Z,l}}{\Vert {\rho }_{l,\mathbf{\theta }}(\mathbf{x}{)}^{-1}-Z_l(\mathbf{x})\Vert }_{\delta }& +\sum _{\mathbf{x}\in {\Omega }_{Z,r}}{\Vert {\rho }_{r,\mathbf{\theta }}(\mathbf{x}{)}^{-1}-Z_r(\mathbf{x})\Vert }_{\delta }\end{array}$$

$\theta$是CNN参数那么预测的深度倒数：${\rho }_{r/l,\theta }$，$\Vert \cdot {\Vert }_{\delta }$是berHu范数，结合了L1和L2范数：
$$\Vert d{\Vert }_{\delta }=\{\begin{array}{l}|d|,d\le \delta \\ \frac{d^2+{\delta }^2}{2\delta },d>\delta \end{array}$$

$$\delta =0.2\underset{\mathbf{x}\in {\Omega }_Z}{\max }\left(\left|\rho (\mathbf{x}{)}^{-1}-Z(\mathbf{x})\right|\right)$$

Unsupervised loss.

$$\begin{array}{c}{\mathcal{L}}_{\mathbf{\theta }}^U={\sum }_{\mathbf{x}\in {\Omega }_{U,l}}\left|\left({\mathbf{G}}_{\sigma }\ast I_l\right)(\mathbf{x})-\left({\mathbf{G}}_{\sigma }\ast I_r\right)\left(\omega \left(\mathbf{x},{\rho }_{l,\mathbf{\theta }}(\mathbf{x})\right)\right)\right|\\ +{\sum }_{\mathbf{x}\in {\Omega }_{U,r}}\left|\left({\mathbf{G}}_{\sigma }\ast I_r\right)(\mathbf{x})-\left({\mathbf{G}}_{\sigma }\ast I_l\right)\left(\omega \left(\mathbf{x},-{\rho }_{r,\mathbf{\theta }}(\mathbf{x})\right)\right)\right|\end{array}$$

${\mathrm{G}}_{\sigma }$是高斯核，模糊是为了去噪，使用$\sigma =1\mathrm{p}\mathrm{x}$

Regularization loss.

$$L_{\mathbf{\theta }}^R=\sum _{i\in \{l,r\}}\sum _{\mathbf{x}\in \Omega }\left|\varphi {\left(\nabla I_i(\mathbf{x})\right)}^{\top }\nabla {\rho }_i(\mathbf{x})\right|$$

$$\varphi (\mathbf{g})={\left(\exp \left(-\eta \left|g_x\right|\right),\exp \left(-\eta \left|g_y\right|\right)\right)}^{\top }$$

$$\eta =\frac{1}{255}$$
防止预测梯度太大作用，个人理解：当预测梯度$\nabla {\rho }_i(\mathbf{x})$很大时，而真实梯度很小，导致$\varphi {\left(\nabla I_i(\mathbf{x})\right)}^{\top }$很大，所以$L_{\mathbf{\theta }}^R$就很大。保持梯度一致性的意思。。。

总损失

$$\begin{array}{l}{\mathcal{L}}_{\mathbf{\theta }}\left(I_l,I_r,Z_l,Z_r\right)={\lambda }_t{\mathcal{L}}_{\mathbf{\theta }}^S\left(I_l,I_r,Z_l,Z_r\right)+\gamma {\mathcal{L}}_{\mathbf{\theta }}^U\left(I_l,I_r\right)+{\mathcal{L}}_{\mathbf{\theta }}^R\left(I_l,I_r\right)\end{array}$$
${\lambda }_t$ 和$\gamma$是权衡参数

网络结构

用的残差网络Flownet

2种残差块：

上投影残差块：

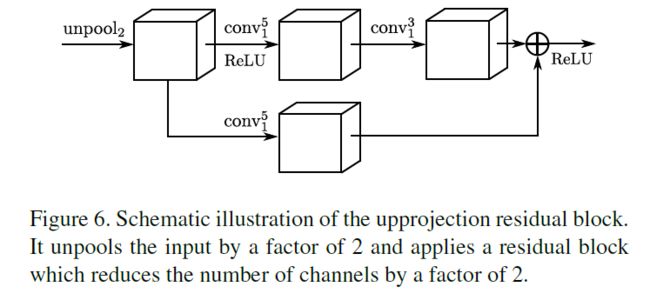
具体网络结构：

四、实验结果

9就是系列2左右约束方法，然后看到本文方法可以结合真实深度预测得到比较精准结果，同时对于真实深度没有扫描的地方，通过CNN进行学习。

五、结论与思考

作者结论

总结

本文在有深度标签数据下是个结合CNN的方法，但是大多数情况是没有深度。要是以后有深度相机集成到手机上，这个方法不失为增强方法。

思考

参考