【读书笔记】【机器学习实战】第七章：集成学习和随机森林

阅读书籍为《Hands-On Machine Learning with Scikit-Learn & TensorFlow》王静源等翻译的中文译版《机器学习实战，基于 Scikit-Learn 和 TensorFlow》

集成学习就是将多种学习模型单独学习的结果综合以获取比单一学习模型更好的结果。也就是所谓三个臭皮匠顶一个诸葛亮的群体智慧的体现。

1.投票分类器VotingClassifier

投票分类器是集成学习最简单的实现办法：聚合每个单独分类器的预测，将投票最多的结果为最终预测类别，这种大多数投票分类器也被称为硬投票分类器。
这里使用卫星数据集，综合三个单独分类器预测，投票产生最佳预测结果，代码如下：

```
from sklearn.datasets import make_moons
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score


log_clf = LogisticRegression()
ran_clf = RandomForestClassifier()
svm_clf = SVC()
tree_clf = DecisionTreeClassifier()

//此处voting=‘hard’意为投票类型为硬投票分类器
voting_clf = VotingClassifier(
    estimators=[('lr', log_clf), ('ran', ran_clf), ('tree', tree_clf)],
    voting='hard'
)

data = make_moons()
X_train = data[0][0:80]
Y_train = data[1][0:80]
X_test = data[0][80:]
y_test = data[1][80:]

for clf in (log_clf, ran_clf, tree_clf, voting_clf):
    clf.fit(X_train, Y_train)
    y_pred = clf.predict(X_test)
    print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
```	

投票分类和单独分类器的对比结果如下：

集成学习为什么会这样呢？最好的解释就是大数定理。
大数定理：假设有一个略有偏倚的硬币，每次抛掷有51%的概率正面向上，49%的概率反面向上，一千次抛掷与概率分布一致，但在一千次后投掷正面向上的概率会达到75%，而且投掷的次数越多，正面向上的概率越大。
大数定理起作用的前提是每次投掷都相互独立这也就要求我们的分类器完全独立。
遗憾的是我们的分类器都使用了同样的数据训练，根本没有办法做到完全独立，就导致了集成的准确率有所降低。

2.bagging和pasting

投票分类器依赖于不同的分类模型进行集成，现在我们要介绍一种依赖于不同训练集的集成方法：bagging和pasting；
这两种基于不同数据集的集成方法的区别在于：
bagging：每次对数据集随机抽样一部分数据进行训练，抽取出来使用过的数据不放回，下次训练在剩下的数据中随机抽取；
pasting：每次对数据集随机抽样一部分数据进行训练，使用过的数据放回，下次训练在完成数据集上随机抽取；

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_moons
from sklearn.metrics import accuracy_score

data = make_moons()
X_train = data[0][0:80]
Y_train = data[1][0:80]
X_test = data[0][80:]
y_test = data[1][80:]

dec_clf = DecisionTreeClassifier()
bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), n_estimators=500,
    max_samples=50, bootstrap=True, n_jobs=-1
)
bag_clf.fit(X_train, Y_train)
dec_clf.fit(X_train, Y_train)
y_pred_D = dec_clf.predict(X_test)
y_pred_b = bag_clf.predict(X_test)
print(bag_clf.__class__.__name__, accuracy_score(y_test, y_pred_b))
print(dec_clf.__class__.__name__, accuracy_score(y_test, y_pred_D))

可以看出单个决策树的正确率为0.85，而500个决策树的正确率上升了0.1：

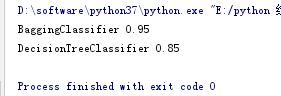
包外评估：
由于数据采集的随机性，有很多数据会被重复使用，而有些数据可能永远不会被采样，一般来说随着数据量的增长，会有37%（对于不同的预测器这是不一样的37%）的数据从未被采样，这些没有采样的数据被称为包外数据。那我们可以很顺手的就用预测器从未见过的这部分包外数据进行模型的检测评估。

bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), n_estimators=200,
    max_samples=50, bootstrap=True, n_jobs=-1,oob_score=True
)
bag_clf.fit(X_train, Y_train)
print(bag_clf.oob_score_)

可以得见和正式训练集上的准确率非常接近：

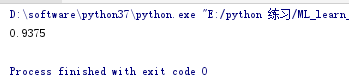
除了仅仅只对数据集随机抽取，这里还有对特征随机抽取的方法：**Random Patches随机子空间法：**可以使用max_features和bootstrap_features替换max_samples和bootstrap，实现对特征的抽取，其他的功能与上面一样，只是我们运算的对象变成了特征而不是实例。此方法适合高维数据集。

3.随机森林

随机森林就是决策树的集成，通常使用bagging方法训练。
除了这种方法还可以直接使用RandomForestClassifier库进行训练：

 Ran_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1)
 Ran_clf.fit(X_train, Y_train)

随机森林之所以称为随机森林是因为：树的节点分裂更加自由，分裂节点时不搜索最好的特征，而是在一个生成的随机特征子集里找最好的一个。
极端随机树：树的节点分裂更加自由，对每个特征使用随机阈值，而不是搜索最佳阈值。由极端随机树组成的森林称为极端随机森林。由于省去了搜索最佳阈值的时间，极端随机树比普通树快的多。
使用from sklearn.tree import ExtraTreeClassifier, ExtraTreeRegressor API接口实现。

除上述一些功能外，随机森林还提供一个特殊的功能：帮助查看特征的重要性。
原理是由于随机森林的树状结构，一般离根越近的特征越重要，所以可以根据树的节点深度估计特征的重要性与否。实现如下：

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
iris = load_iris()
name = ["sepal length", "sepal width", "petal length", "petal width"]

rnd_clf = RandomForestClassifier(n_estimators=500, n_jobs=-1)
rnd_clf.fit(iris["data"], iris["target"])
for name, score, in zip(name, rnd_clf.feature_importances_):
    print(name, score)

4.提升法boosting

是指将几个弱学习器结合成一个强学习器的任意集成方法。
大部分提升法的思路是循环训练预测器，每一次都对上一次做一点改正。目前最流行的方法有二：AdaBoost和梯度提升。

1. AdaBoost
   更加关注（增大错误判断实例的权值）上一次被错误判断的类。从而使新的预测器越来越专注于难缠的问题。
   1.原始条件下，为每一个实例初始化一个权值：
   
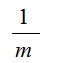
   2.经预测器训练后计算不同实例的加权误差率：
   
   3.根据误差率更新实例权重：
   
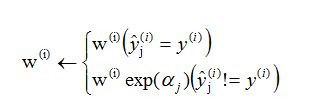
   4.循环提升过程结束后预测：
   
   

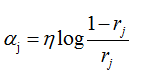
   from sklearn.ensemble import AdaBoostClassifier
   ada_clf = AdaBoostClassifier(
       DecisionTreeClassifier(max_depth=1), n_estimators=200,
       algorithm="SAMME.R", learning_rate=0.5
   )
   
   ada_clf.fit(X_train, Y_train)
   y_pred = ada_clf.predict(X_test)
   print(accuracy_score(y_test, y_pred))
   

2. 梯度提升（后面的调整和限制看的不是很明白，后期再慢慢理解吧）
   与AdaBoost不同，梯度提升的原理是让新的预测器针对上一个预测器的残差进行拟合。

   from sklearn.tree import DecisionTreeRegressor
   import numpy as np
   
   m = 100
   x = 4*np.random.rand(m, 1)-2
   y = x**2 + x + 2 + np.random.randn(m, 1)
   
   tree_reg1 = DecisionTreeRegressor(max_depth=2)
   tree_reg1.fit(x,y)
   
   #对第一次残差拟合
   y2 = y - tree_reg1.predict(x)
   tree_reg2 = DecisionTreeRegressor(max_depth=2)
   tree_reg2.fit(x,y2)
   
   #对第二次残差拟合
   y3 = y - tree_reg1.predict(x)
   tree_reg3 = DecisionTreeRegressor(max_depth=2)
   tree_reg3.fit(x,y3)
   
   #最终预测
   y_pred = sum(tree.predict(x) for tree in (tree_reg1, tree_reg2, tree_reg3))
   

   使用库实现：

   gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3, 
   learning_rate=1.0)
   gbrt.fit(X_train, Y_train)
   

5.堆叠法stacking（层叠泛化法）

简单一点来解释：
1.首先将训练集分为两个子集
2.第一个子集来训练第一层预测器
3.用第一层预测器在第二个子集上进行预测。
4.现在每个实例都有三个预测值，用这些所有实例的预测值创建一个新的训练集（三维），并保留目标值。
5.在这个新的训练集上训练混合器。
6.通过这种方法可以训练多种不同学习模型的混合器。于是我们就有一个混合器层。

诀窍就在于将训练集分为三个，第一个训练第一层。第二个用来创造训练第二层的新训练集（通过第一层的预测），第三个用来创造训练第三层的新训练集（使用第二层的预测）。一旦训练完成，我们就可以按照顺序遍历每层来对新实例进行预测。

备注：
在某些情况下可以称为堆叠（stacking），但多数情况下当我们使用留存集进行堆叠时，确切一点应该称为混合(blending)
这个方法看起来仿佛很高效，但并没有库函数，可以参考一些开源代码实现一波。