SLAM基础问题总结（3）

1、推导直接法BA，直接法的分类，三个假设及优劣
$${\mathbf{p}}_1=\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{Z_1}\mathbf{K}\mathbf{P}$$.$${\mathbf{p}}_2=\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{Z_2}\mathbf{K}(\mathbf{R}\mathbf{P}+\mathbf{t})=\frac{1}{Z_2}\mathbf{K}{\left(\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}\right)}_{1:3}$$
优化相机的位姿，来寻找与 p1 更相似的 p2 。这同样可以通过解一个优化问题，但此时最小化的不是重投影误差，而是光度误差（Photometric Error），也就是 P 的两个像素的亮度误差：$$e={\mathbf{I}}_1\left({\mathbf{p}}_1\right)-{\mathbf{I}}_2\left({\mathbf{p}}_2\right)$$在直接法中，假设一个空间点在各个视角下，成像的灰度是不变的。有许多个（比如 N 个）空间点 Pi ，那么，整个相机位姿估计问题变为：$$\underset{\xi }{\min }J(\mathbf{\xi })=\sum _{i=1}^N{e}_i^T{e}_i,e_i={\mathbf{I}}_1\left({\mathbf{p}}_{1,i}\right)-{\mathbf{I}}_2\left({\mathbf{p}}_{2,i}\right)$$给 exp(ξ) 左乘一个小扰动 exp(δξ)，得：$$\begin{array}{rl}e(\mathbf{\xi }\oplus \delta \mathbf{\xi })& ={\mathbf{I}}_1\left(\frac{1}{Z_1}\mathbf{K}\mathbf{P}\right)-{\mathbf{I}}_2\left(\frac{1}{Z_2}\mathbf{K}\exp \left(\delta {\mathbf{\xi }}^{\wedge }\right)\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}\right)\\ & \approx {\mathbf{I}}_1\left(\frac{1}{Z_1}\mathbf{K}\mathbf{P}\right)-{\mathbf{I}}_2\left(\frac{1}{Z_2}\mathbf{K}\left(1+\delta {\mathbf{\xi }}^{\wedge }\right)\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}\right)\\ & ={\mathbf{I}}_1\left(\frac{1}{Z_1}\mathbf{K}\mathbf{P}\right)-{\mathbf{I}}_2\left(\frac{1}{Z_2}\mathbf{K}\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}+\frac{1}{Z_2}\mathbf{K}\delta {\mathbf{\xi }}^{\wedge }\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}\right)\end{array}$$记：$$\begin{array}{rl}\mathbf{q}& =\delta {\mathbf{\xi }}^{\wedge }\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}\\ \mathbf{u}& =\frac{1}{Z_2}\mathbf{K}\mathbf{q}\end{array}$$利用一阶泰勒展开，有：$$\begin{array}{rl}e(\mathbf{\xi }\oplus \delta \mathbf{\xi })& ={\mathbf{I}}_1\left(\frac{1}{Z_1}\mathbf{K}\mathbf{P}\right)-{\mathbf{I}}_2\left(\frac{1}{Z_2}\mathbf{K}\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}+\mathbf{u}\right)\\ & \approx {\mathbf{I}}_1\left(\frac{1}{Z_1}\mathbf{K}\mathbf{P}\right)-{\mathbf{I}}_2\left(\frac{1}{Z_2}\mathbf{K}\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{P}\right)-\frac{\partial {\mathbf{I}}_2}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{q}}\frac{\partial \mathbf{q}}{\partial \delta \xi }\delta \mathbf{\xi }\\ & =e(\mathbf{\xi })-\frac{\partial {\mathbf{I}}_2}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{q}}\frac{\partial \mathbf{q}}{\partial \delta \mathbf{\xi }}\delta \mathbf{\xi }\end{array}$$ ∂I2 /∂u 为 u 处的像素梯度；
∂u/∂q 为投影方程关于相机坐标系下的三维点的导数。$$\frac{\partial \mathbf{u}}{\partial \mathbf{q}}=\left[\begin{array}{ccc}\frac{\partial u}{\partial X}& \frac{\partial u}{\partial Y}& \frac{\partial u}{\partial Z}\\ \frac{\partial v}{\partial X}& \frac{\partial v}{\partial Y}& \frac{\partial v}{\partial Z}\end{array}\right]=\left[\begin{array}{ccc}\frac{f_x}{Z}& 0& -\frac{f_{x}X}{Z^2}\\ 0& \frac{f_y}{Z}& -\frac{f_{y}Y}{Z^2}\end{array}\right]$$∂q/∂δξ 为变换后的三维点对变换的导数：$$\frac{\partial \mathbf{q}}{\partial \delta \mathbf{\xi }}=\left[\mathbf{I},-{\mathbf{q}}^{\wedge }\right]$$推导了误差相对于李代数的雅可比矩阵：$$\mathbf{J}=-\frac{\partial {\mathbf{I}}_2}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{\xi }}$$其中：$$\frac{\partial \mathbf{u}}{\partial \delta \mathbf{\xi }}=\left[\begin{array}{cccccc}\frac{f_x}{Z}& 0& -\frac{f_{x}X}{Z^2}& -\frac{f_{x}XY}{Z^2}& f_x+\frac{f_x{X}^2}{Z^2}& -\frac{f_{x}Y}{Z}\\ 0& \frac{f_y}{Z}& -\frac{f_{y}Y}{Z^2}& -f_y-\frac{f_y{Y}^2}{Z^2}& \frac{f_{y}XY}{Z^2}& \frac{f_{y}X}{Z}\end{array}\right]$$然后使用 G-N 或L-M 计算增量，迭代求解。

直接法分类：

• 稀疏直接法通常我们使用数百个至上千个关键点，并且像 L-K 光流那样，假设它周围像素也是不变的。这种稀疏直接法不必计算描述子，并且只使用数百个像素，因此速度最快，但只能计算稀疏的重构。
• 考虑只使用带有梯度的像素点，舍弃像素梯度不明显的地方。这称之为半稠密（Semi-Dense）的直接法，可以重构一个半稠密结构。
• P 为所有像素，称为稠密直接法。稠密重构需要计算所有像素（一般几十万至几百个），因此多数不能在现有的 CPU 上实时计算，需要GPU 的加速。

直接法完全依靠优化来求解相机位姿。像素梯度引导着优化的方向。如果我们想要得到正确的优化结果，就必须保证大部分像素梯度能够把优化引导到正确的方向。

优点：

• 可以省去计算特征点、描述子的时间。
• 只要求有像素梯度即可，无须特征点。因此，直接法可以在特征缺失的场合下使用。比较极端的例子是只有渐变的一张图像。它可能无法提取角点类特征，但可以用直接法估计它的运动。
• 可以构建半稠密乃至稠密的地图，这是特征点法无法做到的。

缺点：

• 非凸性——直接法完全依靠梯度搜索，降低目标函数来计算相机位姿。其目标函数中需要取像素点的灰度值，而图像是强烈非凸的函数。这使得优化算法容易进入极小，只在运动很小时直接法才能成功。
• 单个像素没有区分度。找一个和他像的实在太多了！——于是我们要么计算图像块，要么计算复杂的相关性。由于每个像素对改变相机运动的“意见”不一致。只能少数服从多数，以数量代替质量。
• 灰度值不变是很强的假设。如果相机是自动曝光的，当它调整曝光参数时，会使得图像整体变亮或变暗。光照变化时亦会出现这种情况。特征点法对光照具有一定的容忍性，而直接法由于计算灰度间的差异，整体灰度变化会破坏灰度不变假设，使算法失败。针对这一点，目前的直接法开始使用更细致的光度模型标定相机，以便在曝光时间变化时也能让直接法工作。

2、什么是闭环检测？常用的方法有哪些？有没有创新？
闭环检测：

• 相机经过了同一个地方，采集到了相似的数据。回环检测的关键，就是如何有效地检测出相机经过同一个地方这件事。可以为后端的 Pose
  Graph 提供更多的有效数据，使之得到更好的估计，特别是得到一个全局一致（GlobalConsistent）的估计。还可以利用回环检测进行重定位。

方法：

• 对任意两张图像都做一遍特征匹配，根据正确匹配的数量确定哪两个图像存在关联。
• Bag-of-Words（BoW）----k-means++、K 叉树字典

创新：

• 是否能对机器学习的图像特征进行聚类，而不是 SURF、ORB 这样的人工设计特征 进行聚类？
• 是否有更好的方式进行聚类，而不是用树结构加上 K-means 这些较朴素的方式？结合目前机器学习的发展，二进制描述子的学习和无监督的聚类，都是很有望在深度学习框架中得以解决的问题。
• HBST：https://gitlab.com/srrg-software/srrg_hbst

3、简单描述Ceres优化库
Ceres 库面向通用的最小二乘问题的求解，Ceres 求解的最小二乘问题最一般的形式如下（带边界的核函数最小二乘）：$$\begin{array}{ll}{\min }_x& \frac{1}{2}{\sum }_i{\rho }_i\left({\Vert f_i\left(x_{i_1},\dots x_{i_n}\right)\Vert }^2\right)\\ \text{ s.t. }& l_j\le x_j\le u_j\end{array}$$核函数 ρ(·)，优化变量为 x1 ,…,xn ，fi 称为代价函数（Cost function），在 SLAM 中亦可理解为误差项。lj 和 uj 为第 j 个优化变量的上限和下限。在 Ceres 中，将定义优化变量 x 和每个代价函数 fi ，再调用 Ceres 进行求解。可以选择使用 G-N 或者 L-M 进行梯度下降，并设定梯度下降的条件，Ceres 会在优化之后，将最优估计值返回

4、描述（扩展）卡尔曼滤波与粒子滤波。
KF：主要参考这篇博客https://blog.csdn.net/u010720661/article/details/63253509

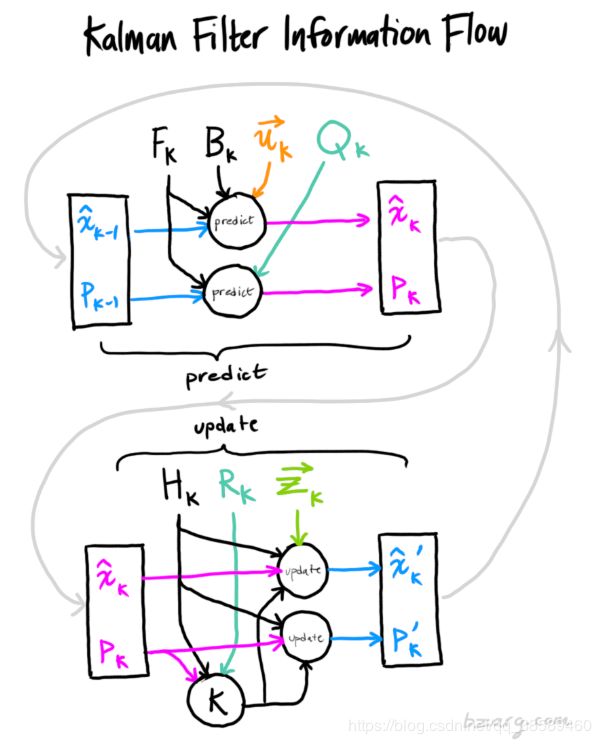
EKF：

• KF主要针对的是线性系统，SLAM 中的运动方程和观测方程通常是非线性函数，尤其是视觉 SLAM中的相机模型，需要使用相机内参模型以及李代数表示的位姿，更不可能是一个线性系统。
• 一个高斯分布，经过非线性变换后，往往不再是高斯分布，所以在非线性系统中，必须取一定的近似，将一个非高斯的分布近似成一个高斯分布。

把卡尔曼滤波器的结果拓展到非线性系统中来，称为扩展卡尔曼滤波器（Ex-tended Kalman Filter，EKF）。通常的做法是，在某个点附近考虑运动方程以及观测方程的一阶泰勒展开，只保留一阶项，即线性的部分，然后按照线性系统进行推导。令 k−1 时刻的均值与协方差矩阵为：

$${\hat{\mathbf{x}}}_{k-1},{\hat{\mathbf{P}}}_{k-1}$$卡尔曼增益${\mathbf{K}}_k$$${\mathbf{K}}_k={\overline{\mathbf{P}}}_k{\mathbf{H}}^{\mathrm{T}}{\left(\mathbf{H}{\overline{\mathbf{P}}}_k{\mathbf{H}}^{\mathrm{T}}+{\mathbf{Q}}_k\right)}^{-1}$$预测和更新方程：$${\hat{\mathbf{x}}}_k={\overline{\mathbf{x}}}_k+{\mathbf{K}}_k\left({\mathbf{z}}_k-h\left({\overline{\mathbf{x}}}_k\right)\right),{\hat{\mathbf{P}}}_k=\left(\mathbf{I}-{\mathbf{K}}_k\mathbf{H}\right){\overline{\mathbf{P}}}_k$$
EKF的局限：

• 滤波器方法在一定程度上假设了马尔可夫性，也就是 k 时刻的状态只与 k −1时刻相关，而与 k − 1 之前的状态和观测都无关。如果当前帧确实与很久之前的数据有关（例如回环），那么滤波器就会难以处理这种情况。
• EKF 滤波器仅在 ${\hat{\mathbf{x}}}_{k-1}$处做了一次线性化，但一阶泰勒展开并不一定能够近似整个函数。如果系统有强烈的非线性，那线性近似就只在很小范围内成立，不能认为在很远的地方仍能用线性来近似。这就是 EKF 的非线性误差，是它的主要问题所在。
• 从程序实现上来说，EKF 需要存储状态量的均值和方差，并对它们进行维护和更新。如果把路标也放进状态的话，由于视觉 SLAM 中路标数量很大，这个存储量是相当可观的，且与状态量呈平方增长（因为要存储协方差矩阵）。因此，EKF SLAM 普遍被认为不可适用于大型场景。

通常认为，在同等计算量的情况下，非线性优化能取得更好的效果。
粒子滤波：
主要参考博客：https://blog.csdn.net/piaoxuezhong/article/details/78619150

未完待续。。。。