SVM学习笔记
分析转载自:https://zhuanlan.zhihu.com/p/28660098 & https://blog.csdn.net/arthur503/article/details/19966891
什么是线性分类器?
可以把两种不同类别样本分开的线性模型(或者超平面)。
什么是最大间隔分类器?
所有线性分类器(或者超平面)中,可以把不同类别样本分的最开的那个。
什么是支持向量机?
对于线性可分两类数据,支持向量机就是条直线(对于高维数据点就是一个超平面),。两类数据点中的的分割线有无数条,SVM就是这无数条中最完美的一条,可以把不同类别样本分的最开。
怎么样才算最完美呢?
就是这条线距离两类数据点越远,则当有新的数据点的时候我们使用这条线将其分类的结果也就越可信。
- 我们需要先找到数据点中距离分割超平面距离最近的点(找最小)
- 然后尽量使得距离超平面最近的点的距离的绝对值尽量的大(求最大)
什么是支持向量?
距离分割平面最近的点。
总结:
支持向量机就是用来分割数据点那个分割面,他的位置是由支持向量确定的(如果支持向量发生了变化,往往分割面的位置也会随之改变), 因此这个面就是一个支持向量确定的分类器即支持向量机。
SVM的分类:
1.硬间隔支持向量机:
硬间隔分类即线性可分支持向量机。假设直线为y=wx+b,那么只要使所有正分类点到该直线的距离与所有负分类点到该直线的距离的总和达到最大,这条直线就是最优分类直线。这样,原问题就转化为一个约束优化问题,可以直接求解。这叫做硬间隔最大化,得到的SVM模型称作硬间隔支持向量机。
2.软间隔支持向量机:
软间隔分类即线性不可分支持向量机。利用软间隔分类时是因为存在一些训练集样本不满足函数间隔(泛函间隔)大于等于1的条件(个别噪声点),于是加入一个非负的参数 C(松弛变量),让得出的函数间隔加上 C 满足条件。通过加入松弛变量,在原距离函数中需要加入新的松弛变量带来的误差,这样,最终的优化目标函数变成了两个部分组成:距离函数和松弛变量误差。如果我们能够容忍噪声,那就把C调小,让他的权重降下来,从而变得不重要;反之,我们需要很严格的噪声小的模型,则将C调大一点,权重提升上去,变得更加重要。通过对参数C的调整,可以对模型进行控制。这叫做软间隔最大化,得到的SVM称作软间隔支持向量机。
3.非线性支持向量机:
硬间隔支持向量机和软间隔支持向量机都是解决线性可分数据集或近似线性可分数据集的问题的。
但是如果噪点很多,甚至会造成数据变成了线性不可分的。
思想:对于在N维空间中线性不可分的数据,在N+1维以上的空间会有更大到可能变成线性可分的,但并不是一定会在N+1维上线性可分。维度越高,线性可分的可能性越大。
对于线性不可分的数据,我们可以将它映射到线性可分的新空间中,之后就可以用刚才说过的硬间隔支持向量机或软间隔支持向量机来进行求解了。
高斯核函数对应的支持向量机是高斯径向基函数(RBF),是最常用的核函数。作用就是把数据映射到线性可分的新空间中。
RBF核函数可以将维度扩展到无穷维的空间,因此,理论上讲可以满足一切映射的需求。原因是:RBF对应的是泰勒级数展开,在泰勒级数中,一个函数可以分解为无穷多个项的加和,其中,每一个项可以看做是对应的一个维度,这样,原函数就可以看做是映射到了无穷维的空间中。
总结2:
对于线性不可分的数据,可以通过RBF等核函数来映射到高维,甚至无穷维的空间中而变得线性可分。通过计算间隔和松弛变量等的最大化,可以对问题进行求解。
求解支持向量机
就是求解分割超平面。
将一维直线和二维平面拓展到任意维, 分割超平面可以表示成:
其中 和 就是SVM的参数,不同的 和 确定不同的分割面。
根据数据点到分割超平面的距离公式:
可见,在距离公式中有两个绝对值,其中分母上是常量,分子上则是与数据点相关的。
如果数据点在分割平面上方, ; 数据点在分割平面下方, 。
这样我们在表示任意数据点到分割面的距离就会很麻烦,但是我们通过将数据标签设为+1/-1来讲距离统一用一个公式表示:
当数据点在分割面上方时, , 且数据点距离分割面越远 越大,
当数据点在分割面下方时, , , 且数据点距离分割面越远 越大。
目标函数
我们现在已经有了间隔的公式,我们需要找到一组最好的 和 确定的分割超平面使得支持向量距离此平面的间隔最大。
在数据点中找到距离分割平面最近的点(支持向量),然后优化w和b来最大化支持向量到分割超平面的距离。
等比例改变参数 和
首先看下分割超平面的一个性质。当我们等比例的扩大或缩小ww和bb并不会改变超平面的位置。例如对于位于三维空间中的二维平面 , , ,我们扩大或者缩小 和 并不会影响平面,即 与原始平面相同。
这样我们就可以任意等比例修改参数,来使我们优化的目标表达起来更加友好。
几何间隔和函数间隔
- 函数间隔(Functional Margin):
- 几何间隔(Geometry Margin):
可见由于我们可以等比例的改变参数,函数间隔相当于参数都乘上了 。
目标函数:
subject to
其中 是支持向量到超平面的函数间隔。
我们将所有参数 和 除以 ,便有 , 于是有:
subject to
将最大化问题转换为求最小值:
subject to
这便是一个线性不等式约束下的二次优化问题, 使用拉格朗日乘子法来获取我们优化目标的对偶形式。
通过拉格朗日乘子法和KKT条件将约束条件放入到目标函数中
拉格朗日乘数法是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这样我们可以将我们带约束的目标函数通过拉格朗日乘子法将约束放入到目标函数中方便优化。KKT条件是拉格朗日乘子法在约束条件为不等式的一种延伸。下面我就对拉格朗日乘子法和KKT条件进行下简单总结。
拉格朗日乘子法和KKT条件
我们从无约束优化到带有不等式约束条件逐渐介绍下几种不同类型的优化问题。
无约束优化问题
对于无约束优化问题
梯度 是局部最小点的必要条件,这样,优化问题的求解变成了对该必要条件解方程组。
带等式约束的优化问题
添加了等式限制条件,优化函数为: , subject to
拉格朗日乘子法就是通过引入新的位置变量(拉格朗日橙子)将上式的约束条件一起放到目标函数中:
subject to
通过求解方程组: 便可得到局部最小值的必要条件。
拉格朗日乘子法原理
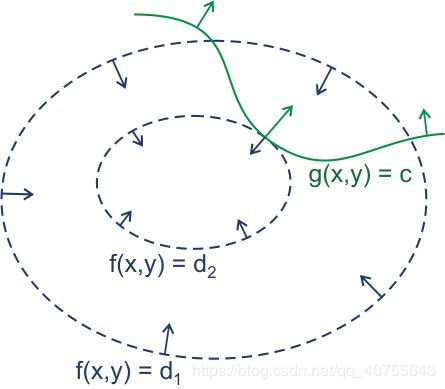
我在这里稍微总结下Lagrange Multiplier的原理吧。
参考上图(忽略函数形式的差异),当约束条件 与 的等高线相切的时候,切点具有局部最优值。此时 的梯度与 梯度同向,我们可以加入一个参数 ,得到他们之间的关系:
上式便是对 求梯度等于0的结果, 这也就是拉格朗日函数了,其中那个关联梯度方向的 就是拉格朗日乘子.
KKT条件
KKT条件是对于有不等式和等式约束的最优化问题具有局部最优解的必要条件。
因为是我们现在的SVM目标函数只有不等式约束没有等式约束,我们可以将优化问题写成:
subject to (这里我们列出两个约束条件)
对应的拉格朗日函数:
则KKT条件(具有局部最优点的必要条件)为:
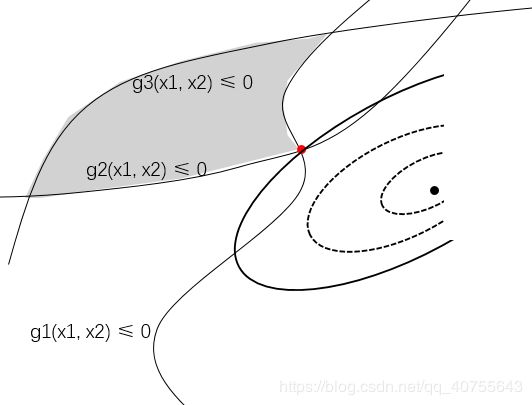
不等式约束边界与目标函数的交接点不一定是切点了,如下图,如果两个不等式同时活跃(起作用),则约束条件与等高线相遇的点是在顶点上。
等式约束函数和目标函数在切点的梯度方向同向,而不等式约束则有目标函数的梯度是约束函数在最优点的负梯度的线性组合(上图的红线和绿线), 于是我们便有约束和目标函数梯度的关系:
其中 , 。
当然,最优点一定是在约束条件那条线上的,也就是满足
但是嘞,有的时候在最优点,不是所有的约束条件都起作用的。
对于有约束优化:
subject to , ,
如上图所示, 约束条件并没有起作用,因此对于有三个约束条件的问题我们的另一个必要条件还可以写成:
为了统一表示,我们可以写成:
由于 ,
- 当约束条件 不起作用时,,便得到了与 相同的条件。
- 当约束条件起作用时,
SVM的拉格朗日函数
上面对拉格朗日乘子法和KKT条件进行了简单的总结,下面我们将其应用在SVM目标函数上。
我们现在求解SVM,是要进行带约束的优化问题:
subject to
对应的拉格朗日函数:
其中,
令 ,则有 .
- 如果 , 根据KKT条件 , 推出 , 则约束 是一个有效约束(active constraint), 对应的 为支持向量
- 如果 , 即 , 为不起作用的约束,对应的 不是支持向量
可见,支持向量对应的约束为活动约束, 我们的目标函数是由支持向量决定的,毕竟我们就是支持向量机嘛.
对偶形式
接下来我们要获取目标函数的对偶问题,通过求解对偶问题的解来获取逼近SVM最优解的解。
我们的目标是求 的最大值,因此我们先把 看成是 的函数,通过梯度为零获取获取极小值的必要条件:
- 对于 : ,得到
我们可以看到,最终的参数 是输入向量的线性组合, 就是其权重 - 对于 :
将上面的到的式子回代,得到对偶形式:
对偶问题:
subject to
关于对偶问题,这里我也稍微做下简单的总结。
通过获取优化问题的对偶问题,我们可以通过优化对偶问题来逼近原问题的最优解。就好像我们上面的拉格朗日函数,我们先将函数看作 的函数,求最小值,然后再把函数看成拉格朗日橙子的函数,并求最大值逼近原始问题的最优解。
例如在SVM中的拉格朗日函数为:
其中, 可知,
因此我们需要求 来使得对偶问题的最大值接近原问题的最小值。
Ok. 最终我们的优化目标函数可以写成:
约束条件:
它是一个线性约束条件下多变量二次函数,一旦得到 的解,便可以根据 和 关系求出 ,进而在得到 ,于是我们就可以得到一个最优分割超平面。