计算智能——粒子群优化算法

 

目录

 粒子群优化算法

算法思想

算法实现

算法流程图

算法代码

实验过程

第一组（w,c1,c2)

第二组（sizepop，dim）

参数更改结果展示

实验结果分析

---

粒子群优化算法

算法思想

  粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。

算法实现

1)初始化一群微粒（群体规模为sizepop），包括随机的位置和速度；
2)评价每个微粒的适应度；
3)对每个微粒，将它的适应值和它经历过的最好位置pbest的作比较，如果较好，则将其作为当前的最好位置pbest；
4)对每个微粒，将它的适应值和全局所经历最好位置gbest的作比较，如果较好，则重新设置gbest的索引号；
5)变化微粒的速度和位置；

公式：V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:))

其中：w是惯性权值

         c1和c2是加速因子
6)如未达到结束条件（通常为足够好的适应值或达到一个预设最大代数Gmax），回到2）。

 

算法流程图

算法代码

PSO.m

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的三个参数
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.8  %惯性权重

maxgen=1000;   % 进化次s数  
sizepop=200;   %种群规模1

Vmax=1;       %限制速度围
Vmin=-1;     
popmax=5;    %变量取值范围
popmin=-5;
dim=2;       %适应度函数维数1

func=1;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(func);%画出待优化的函数，只画出二维情况作为可视化输出

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,dim);    %初始种群
    V(i,:)=Vmax*rands(1,dim);             %初始化速度
                                     %计算适应度
    fitness(i)=fun(pop(i,:),func);   %粒子的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
gbest=pop(bestindex,:);   %全局最佳
pbest=pop;                %个体最佳
fitnesspbest=fitness;     %个体最佳适应度值
fitnessgbest=bestfitness; %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    fprintf('第%d代，',i);
    fprintf('最优适应度%f\n',fitnessgbest);

    for j=1:sizepop
        
        %速度更新
        V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:)); %根据个体最优pbest和群体最优gbest计算下一时刻速度
        V(j,find(V(j,:)>Vmax))=Vmax;   %限制速度不能太大
        V(j,find(V(j,:)popmax))=popmax;%坐标不能超出范围
        pop(j,find(pop(j,:)0.98                         %加入变异种子，用于跳出局部最优值
            pop(j,:)=rands(1,dim);
        end
        
        %更新第j个粒子的适应度值
        fitness(j)=fun(pop(j,:),func); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnesspbest(j)
            pbest(j,:) = pop(j,:);
            fitnesspbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnessgbest
            gbest = pop(j,:);
            fitnessgbest = fitness(j);
        end
    end 
    yy(i)=fitnessgbest;    
        
end
%% 结果分析
figure;
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

Drawfunc.m

function Drawfunc(label)

x=-5:0.05:5;%41列的向量
if label==1
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==2
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Schaffer([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==3
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Griewank([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end



    

fun.m

function y = fun(x,label)
%函数用于计算粒子适应度值
%x           input           输入粒子 
%y           output          粒子适应度值 
if label==1
    y=Rastrigin(x);
elseif label==2
    y=Schaffer(x);
else
    y= Griewank(x);
end

Griewank.m

function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人：
%编制日期：
[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
    y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;

Schaffer.m

function y=Schaffer(x)

[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;

实验过程

本实验将五个参数c1,c2,w,sizepop,dim 分成两组进行测试，以寻找参数的合理设置和参数更改对算法的影响

每个参数的调整都运行了10遍，将得到的最优适应度结果取平均以考量其影响，这里只展示其中的6次结果

第一组（w,c1,c2)

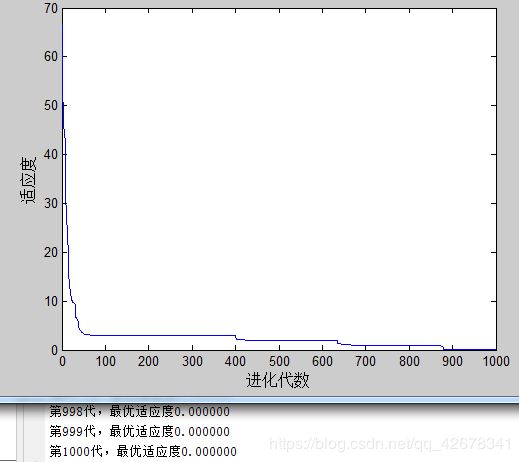
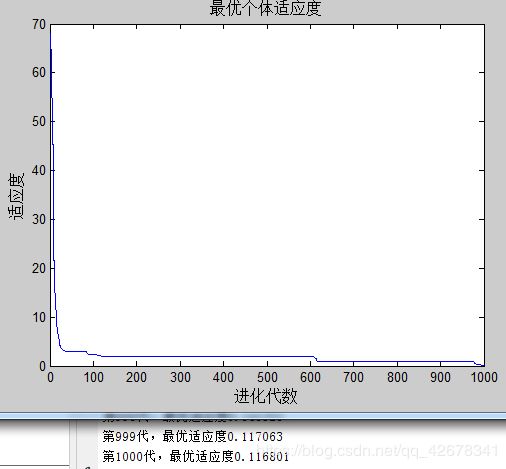
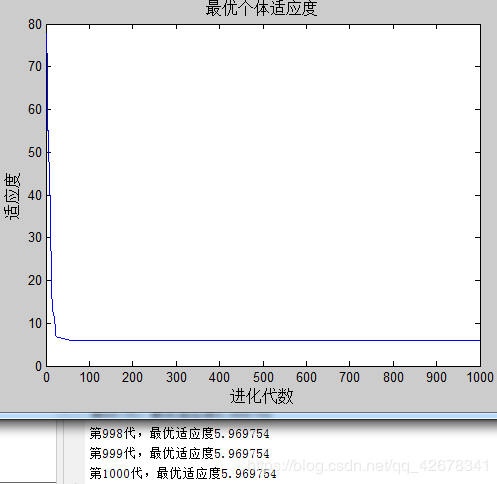
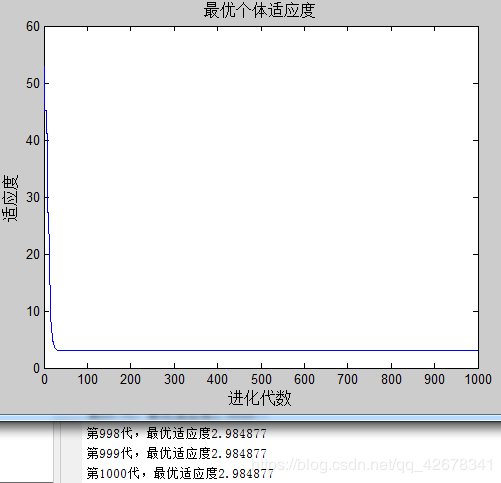
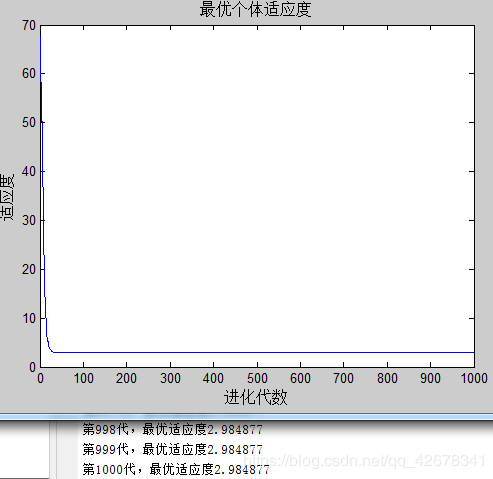
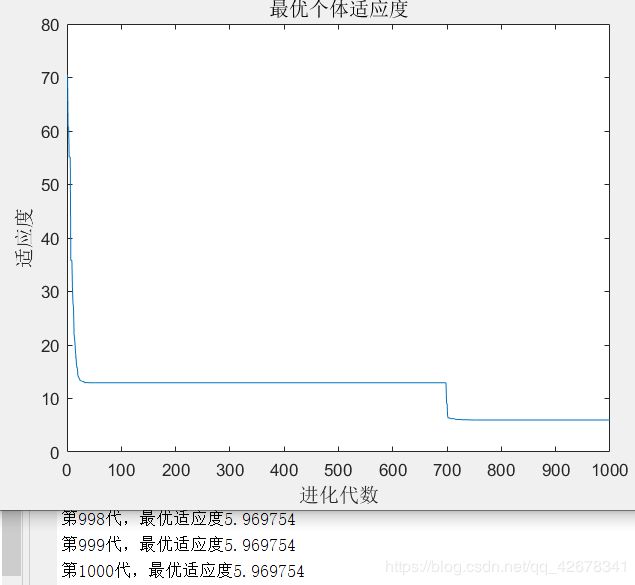
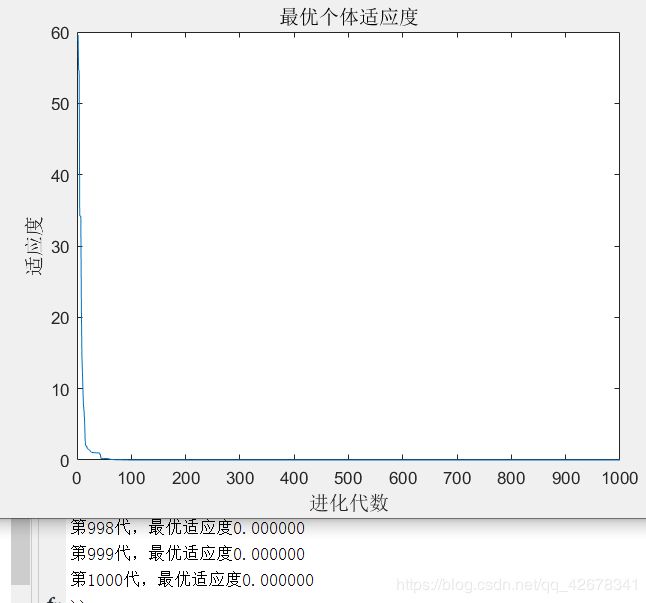
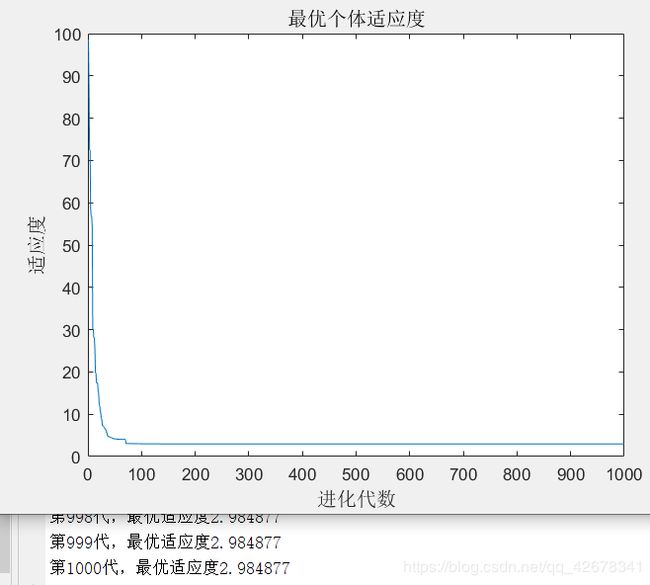
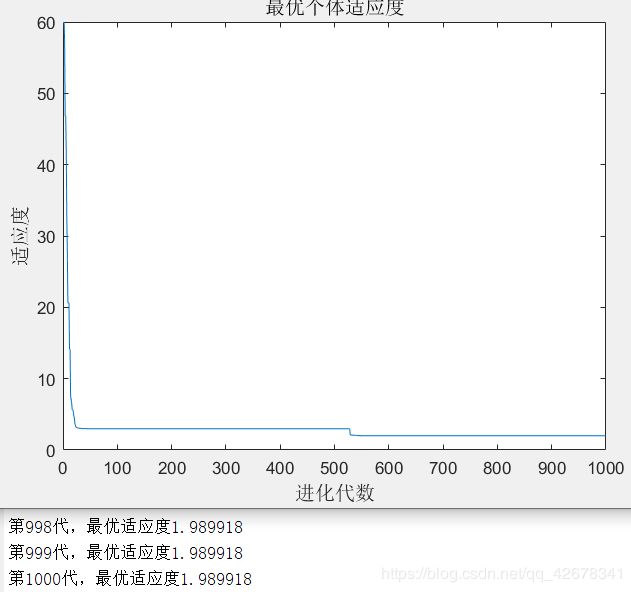
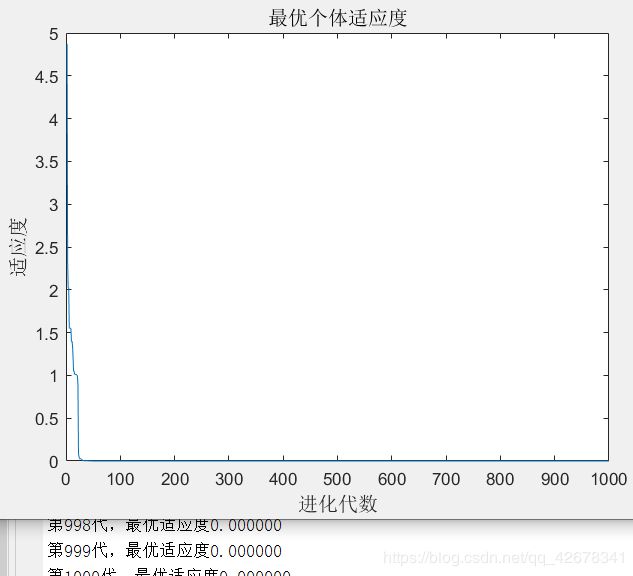
1.c1 = 1.49445;c2 = 1.49445;w=0.4~0.8

说明：设置c1与c2不变，让惯性权重w逐代递减

实验结果

分析：通过设置参数惯性权重w逐代线性递减可以看出，

当惯性权重在初期比较大时，粒子的移动速度多受之前移动速度的影响；

当惯性权重在多代之后变得越来越小，粒子的原移动速度对当前移动速度的影响较小，粒子比较不容易陷入局部最优

 

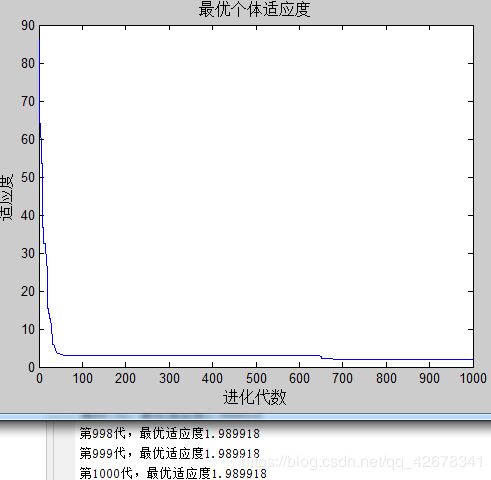
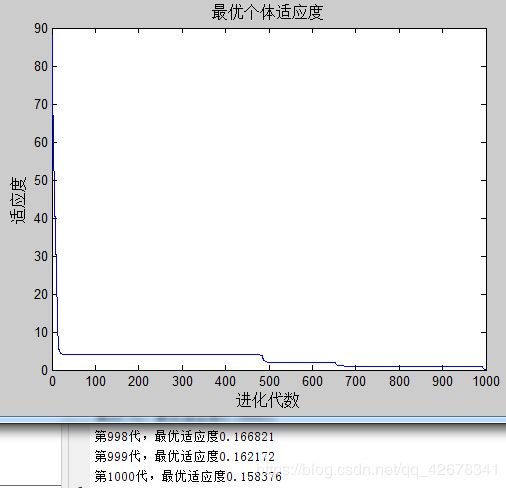
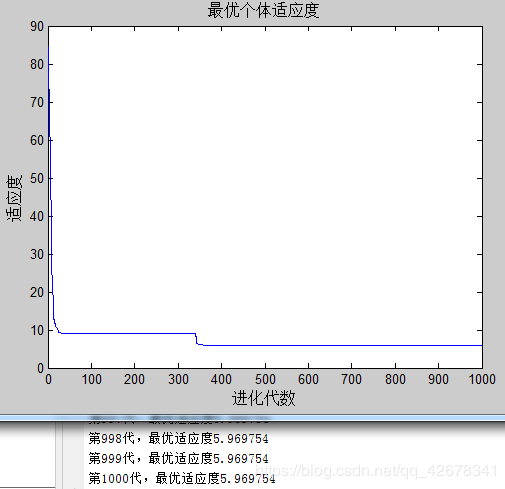
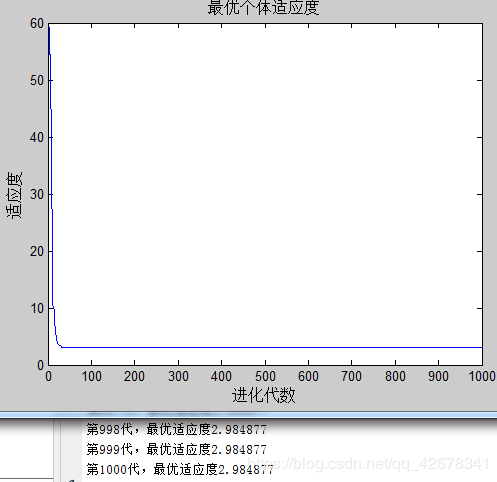
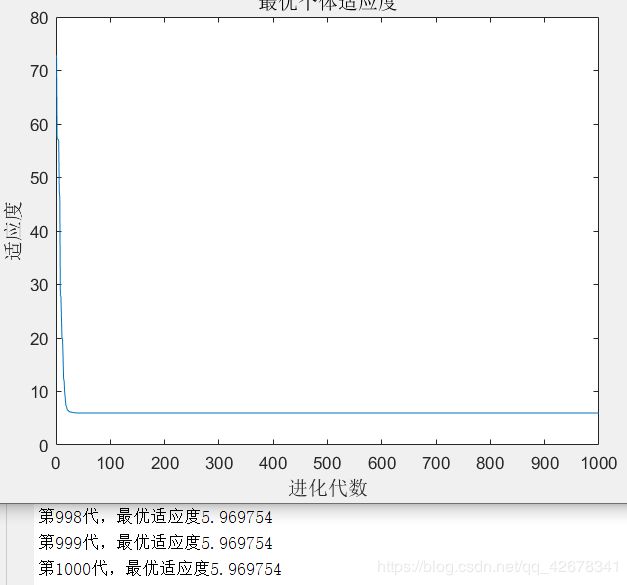
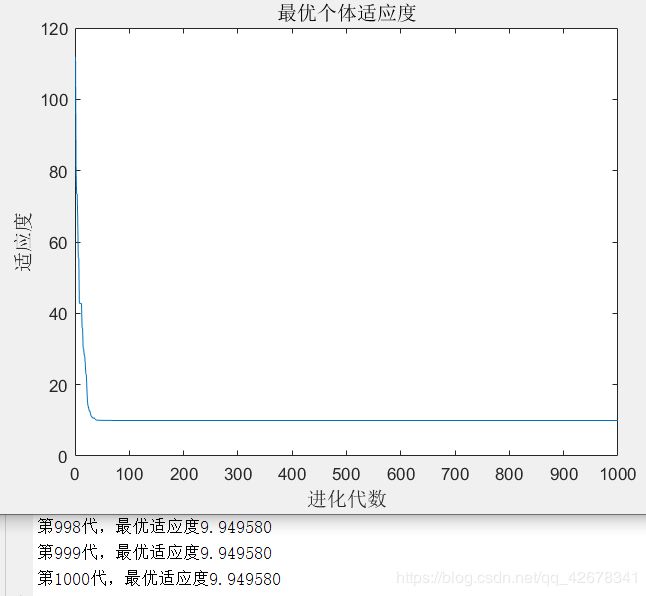
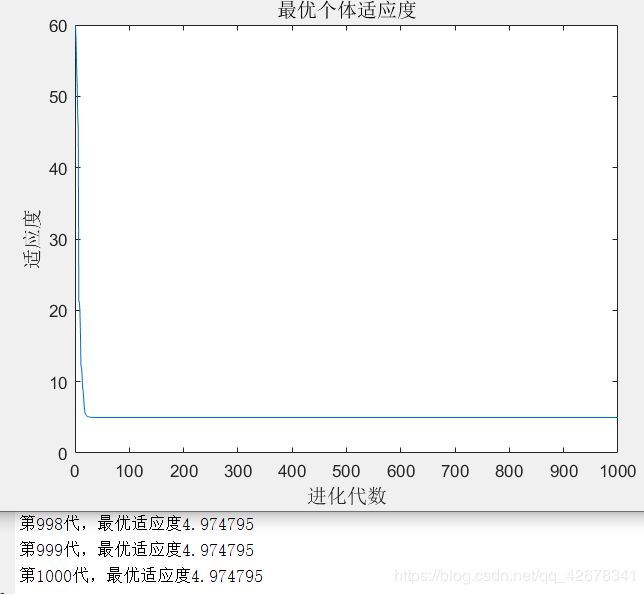
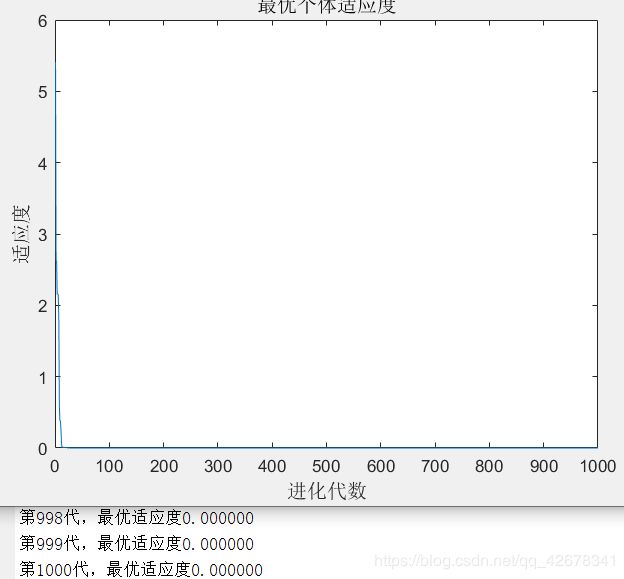
2.c1 = 1.49445;c2 = 1.49445;w=0.6~0.9

说明：设置c1与c2不变，让惯性权重w逐代递减

 

 

 

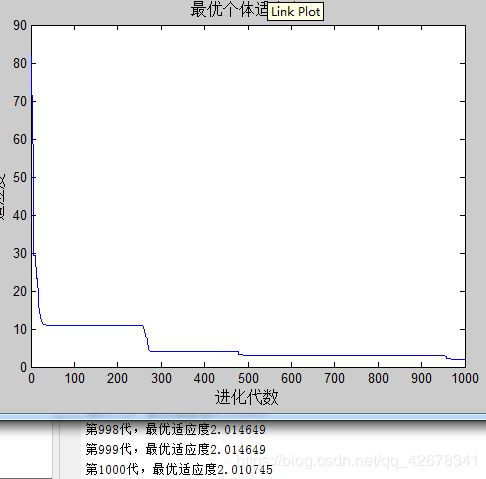
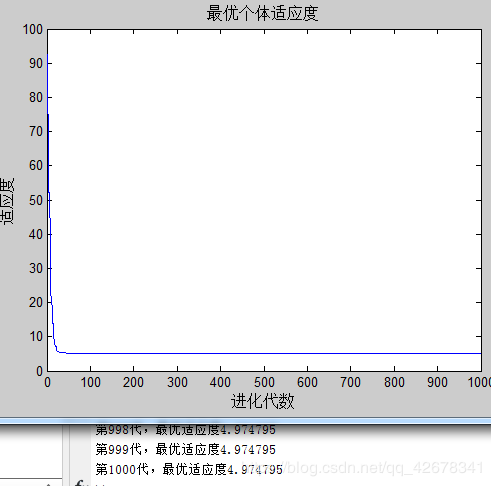
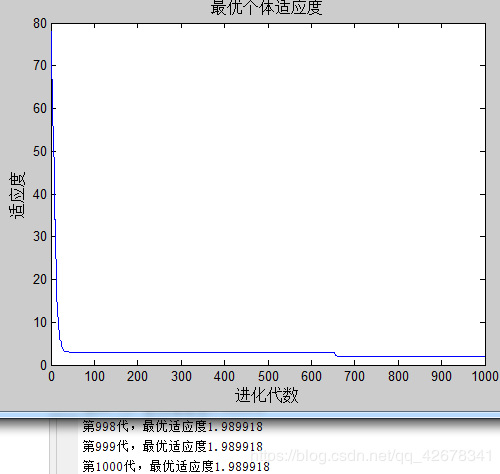
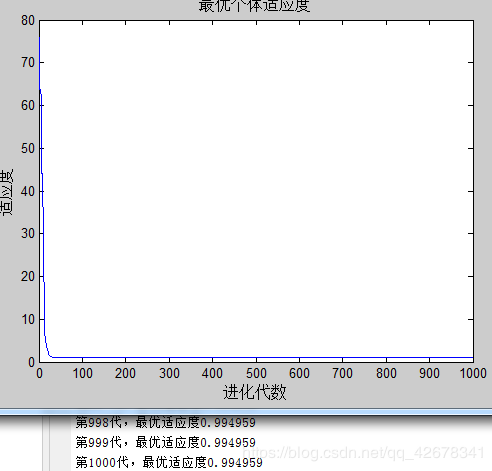
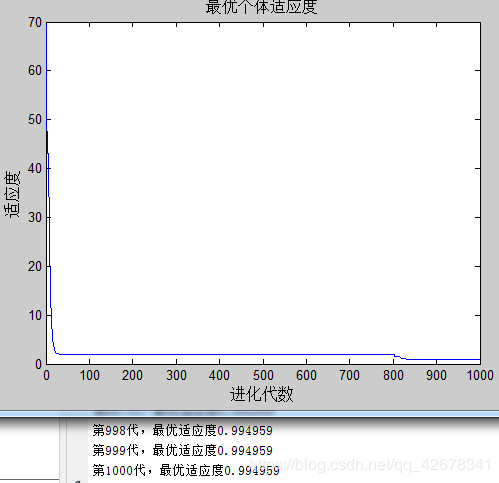
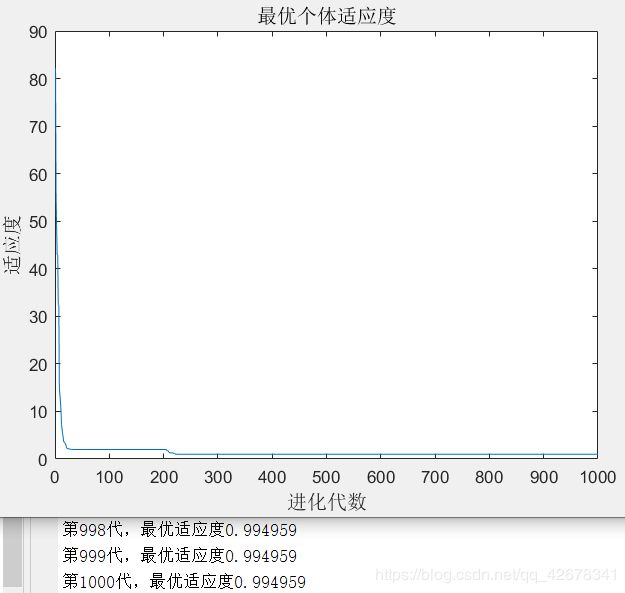
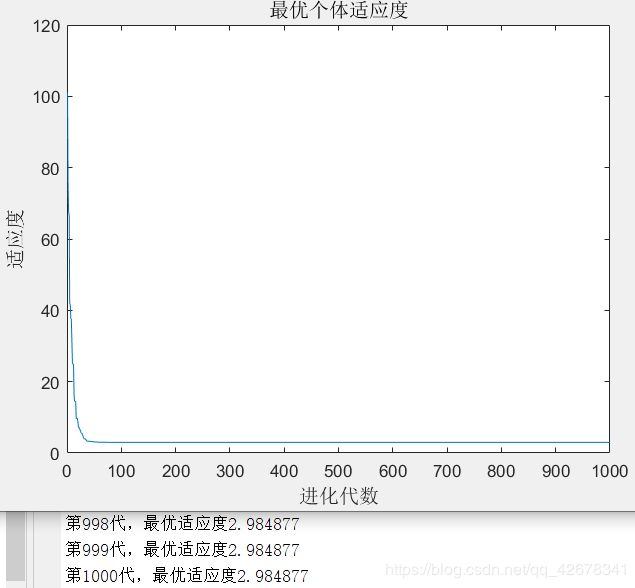
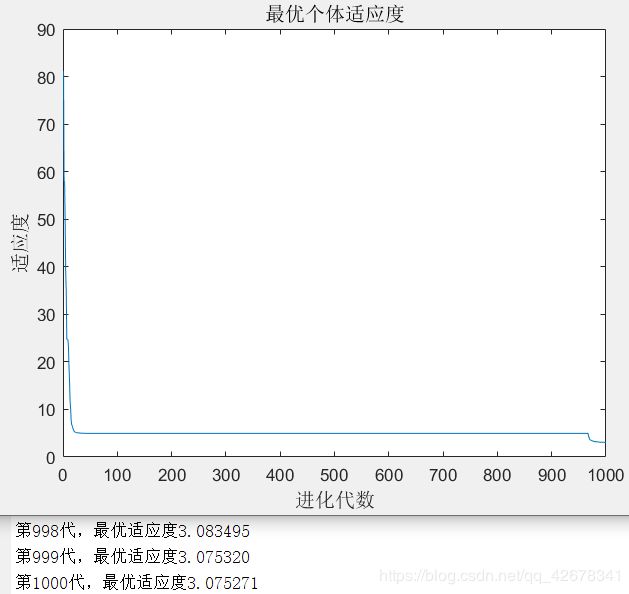
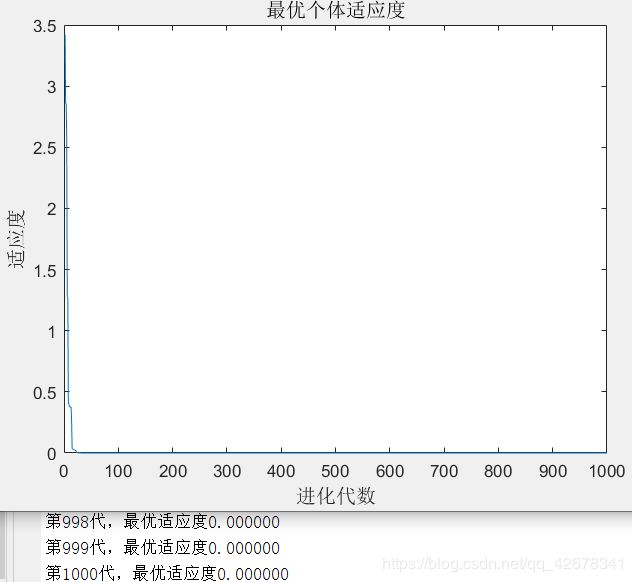
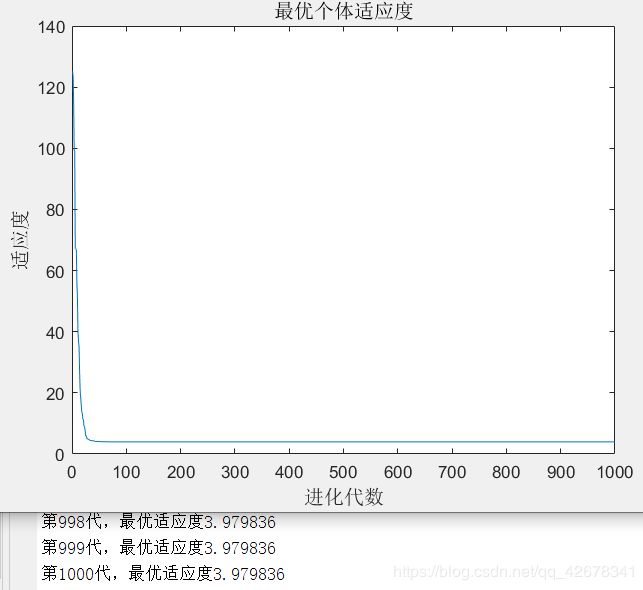
3.c1 = 1~2 ;c2 = 1.49445;w=0.8

说明：设置w与c2不变，让加速因子c1逐代递减

 

分析：通过设置参数加速因子c1逐代线性递减可以看出，

当加速因子c1在初期较大时，粒子会更加偏向自身的极值；

当加速因子c1在多代之后变得越来越小，粒子就会减小对自身极值的依赖，这样容易摆脱局部最优。

 

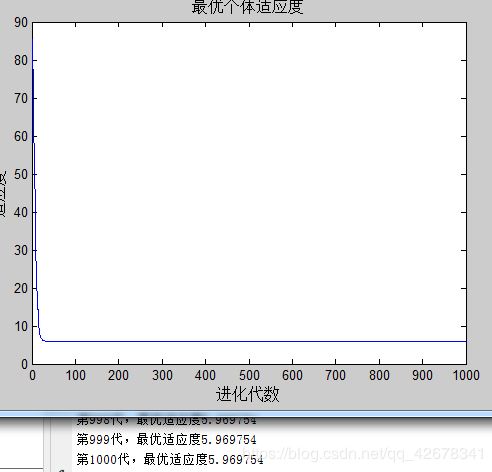
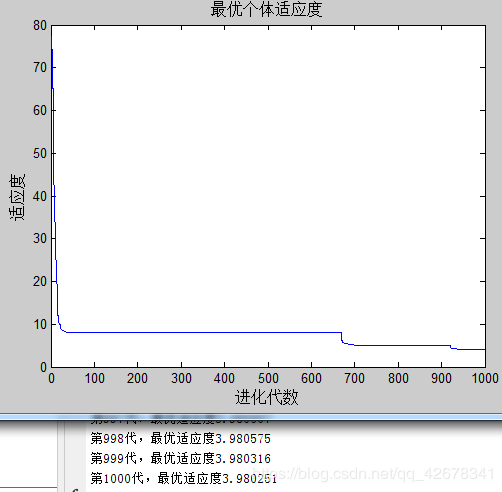
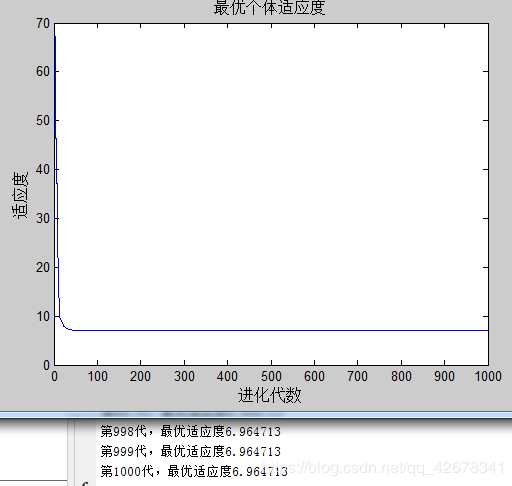
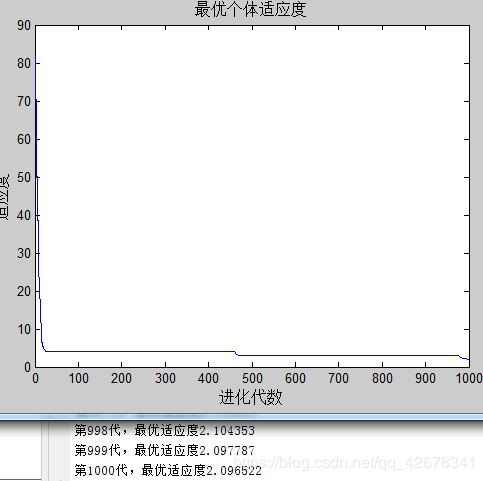
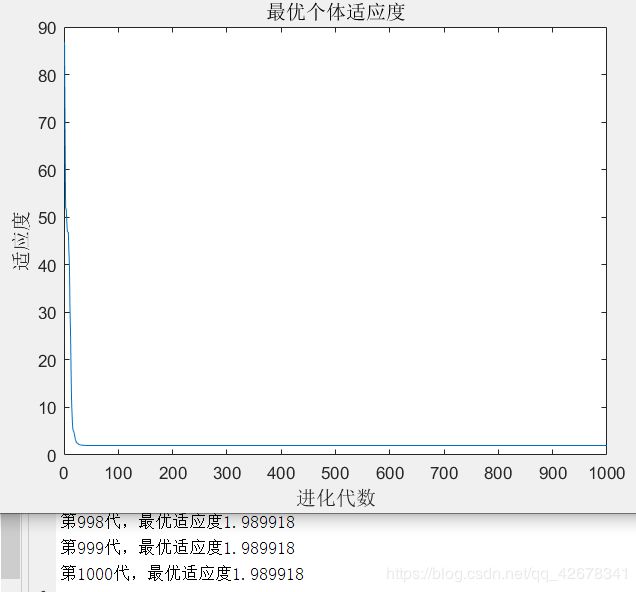
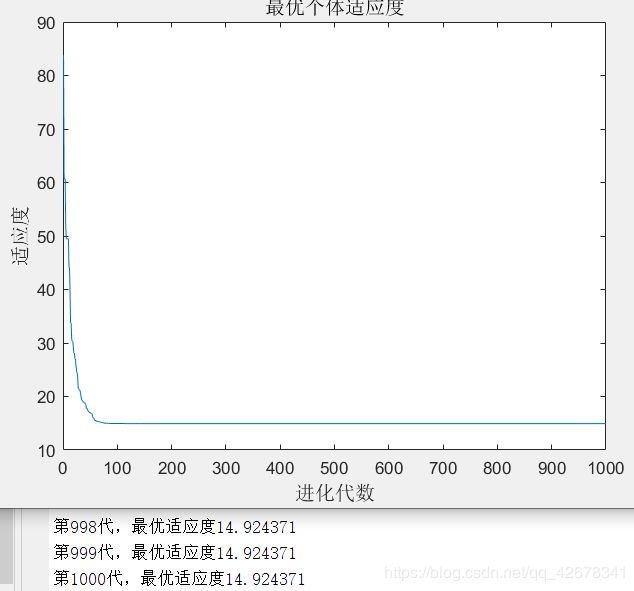
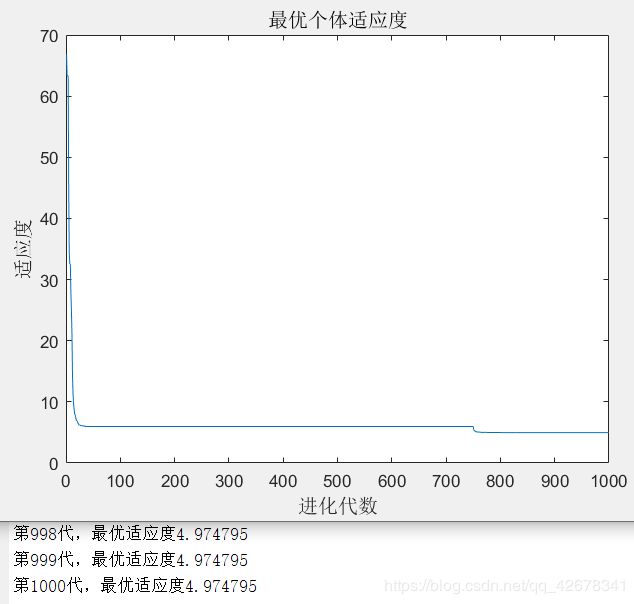
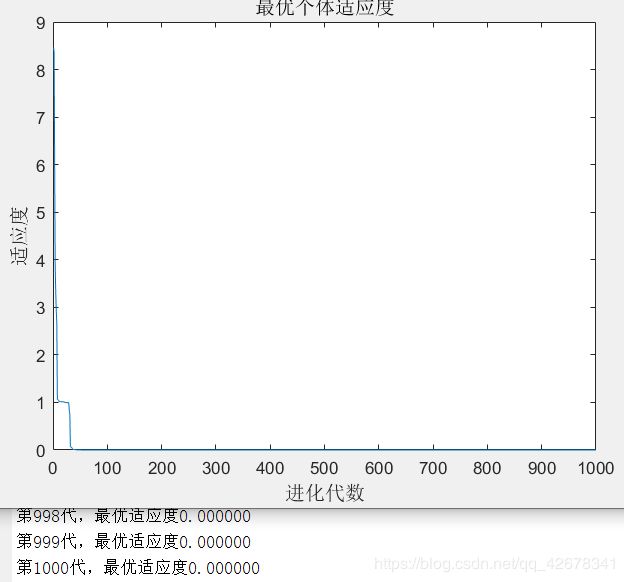
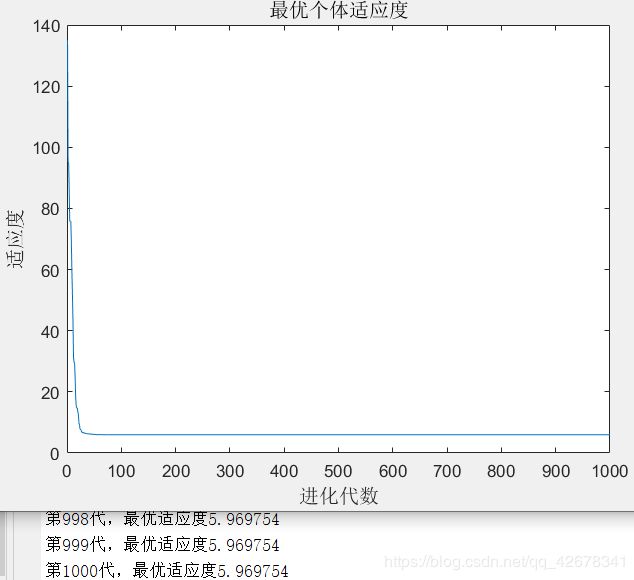
4.c1 = 1.49445 ; c2  = 1~2 ;w = 0.8

说明：设置w与c1不变，让加速因子c2逐代递增

 

分析：通过设置参数加速因子c2逐代线性递增可以看出，

当加速因子c2在初期较小时，粒子对全局极值的推进会较慢；

当加速因子c2在多代之后变得越来越大，粒子就会增加对全局极值的加速推进。

 

第二组（sizepop，dim）

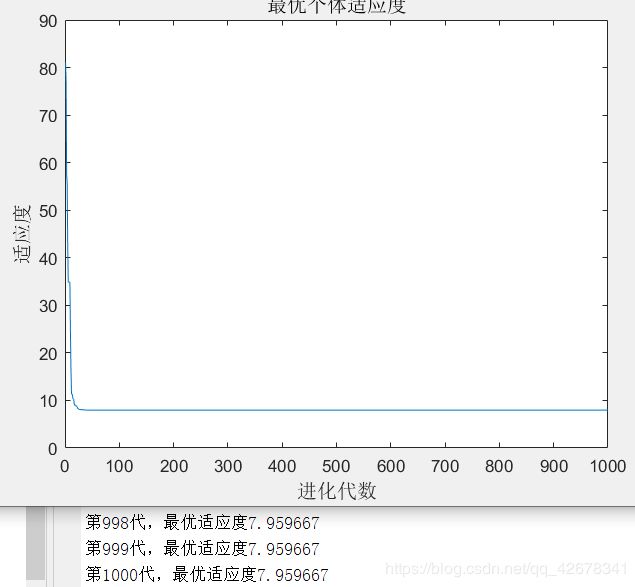
1.Sizepop = 200；dim = 10;

 

 

 

 

2.Sizepop = 50；dim = 10;

 

 

 

3.Sizepop = 400；dim = 10;

 

 

分析：通过更改参数 种群规模sizepop 可以看出，种群规模影响着算法的搜索能力和计算量，

当种群规模较小时，算法能够快速的完成搜索，用时较短；

当种群规模较大时，算法的运行时间也会更长。

 

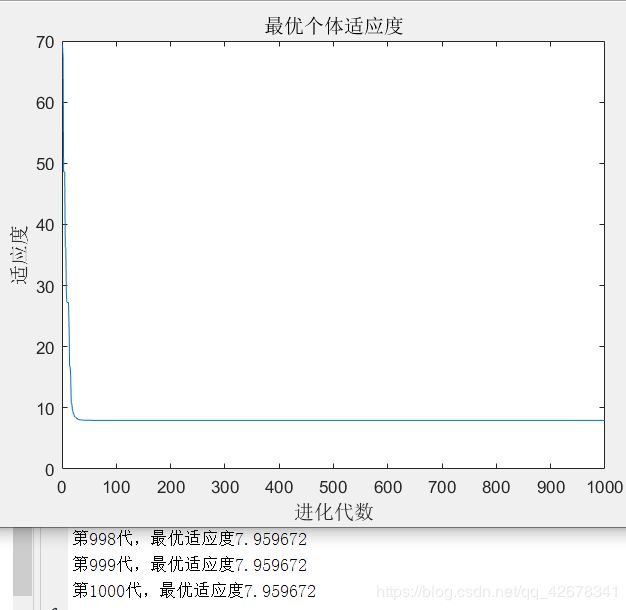
4.Sizepop = 200；dim = 3;

 

 

5.Sizepop = 200；dim = 15;

 

分析：通过更改参数 适应度函数维数dim 可以看出，

当维数较少时，函数复杂性较低，粒子的搜索速度和搜索结果都是特别优异的；

当维数较多时，待搜索的函数复杂度较高，粒子的搜索速度较慢，也容易陷入局部最优。

参数更改结果展示

各参数结果展示

	平均最优适应度
c1 = 1.49445;c2 = 1.49445;w=0.4~0.8	1.212348
c1 = 1~2 ;c2 = 1.49445;w=0.8	2.076157
c1 = 1.49445 ;c2 = 1~2 ;w = 0.8	1.974352
sizepop = 50；dim = 10;	7.846987
sizepop = 200；dim = 10;	2.512741
sizepop = 400；dim = 10;	3.894112
sizepop = 200；dim = 3;	0.000000
sizepop = 200；dim = 10;	2.512741
sizepop = 200；dim = 15;	6.178924

实验结果分析

1. 种群规模sizepop影响着算法的搜索能力和计算能力，一般取值100~200都是可行的
2. 惯性权重w控制着前一速度对当前速度的影响，用于平衡算法的探索和开发能力，设置w线性递减有利于实验结果
3. 加速因子c1和c2代表了粒子向自身极值和全局极值推进的加速权值，设置加速因子c1线性递减同时设置加速因子c2线性递增，可以动态平衡算法的多样性和收敛性
4. 适应度函数维数dim影响适应度函数的复杂性，也直接影响到粒子的搜索速度和效率。