《神经网络与深度学习》 第一章读书笔记

投入情感是精通技艺的关键！

---

感知器

第一节内容非常的简单，定义了一种感知器。介绍了感知器的定义和权重、阈值的概念。然后根据
b=-threshold，用偏置来代替阈值。
我们可以通过设计学习算法能自动调整人工神经元的权重和偏置，自动响应外部的刺激。

---

S型神经元

S型神经元和感知器类似，但是被修改为权重和偏置的微小变化只会引起输出的微小变化。

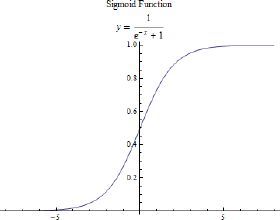
其实这个形状是阶跃函数平滑后的版本。
利用S的平滑性质，我们可以得到一个平滑的感知器。他的平滑意味着权重和偏置的微小变化，然后产生一个输出OUT。然后根据微积分可以将输出表示为一个权重和偏置的线性函数形式。

---

神经网络的结构

输入层、输出层，和隐含层，作者这里很有意思，“隐藏这一术语也许听上去很神秘，但是它仅仅意味着‘既非输入也非输出’”。
隐含层的设计堪称一门艺术。相关研究人员已经为他们开发了许多设计最优原则，使得网络和人们最初预想的一样。
目前我们讨论的网络都是上一层的输出作为下一层的输入，这叫前馈神经网络。
当然也存在递归神经网络，但是本书不对其进行研究。

---

设计一个简单的分类手写数字的网络

本节开始进入正题。
识别手写数字主要是两个问题。一是，分割成单个的数字。，二是识别单独的数字。 我们选择集中精力设计一个识别单个数字的神经网络。
我们将使用一个三层神经网络。如图所示

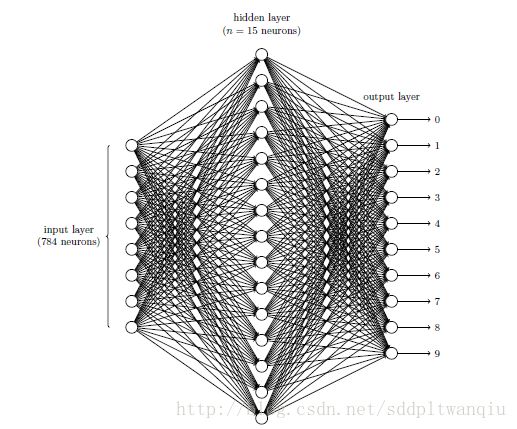
网络的输入层包含给输入像素的值进行编码的神经元。这里是指28*28的手写数字的图像。
第二层是隐藏层。使用n来表示神经元的数量。这里我们先设定为15。
输出层包含10个神经元。然后我们将输出的神经元分别编号为0-9，并计算出哪个神经元具有最高的激活值。然后输出相应的值。
这里作者讲述了一个很重要的思想是为什么不用4个输出神经元。因为2的4次方等于16，完全可以表示数字。但是针对这个特定的问题而言，10个的效果是好于4个的。这是一个启发性的算法，在此附原文：

为了理解为什么我们这么做，我们需要从根本原理上理解神经⽹络究竟在做些什么。⾸先考虑有10 个神经元的情况。我们⾸先考虑第⼀个输出神经元，它告诉我们⼀个数字是不是0。它能那么做是因为可以权衡从隐藏层来的信息。隐藏层的神经元在做什么呢？假设隐藏层的第⼀个神经元只是⽤于检测如下的图像是否存在：

如果所有这四个隐藏层的神经元被激活那么我们就可以推断出这个数字是0。当然，这不是我们推断出0 的唯⼀⽅式——我们能通过很多其他合理的⽅式得到0 （举个例⼦来说，通过上述图像的转换，或者稍微变形）。但⾄少在这个例⼦中我们可以推断出输⼊的数字是0。
假设神经⽹络以上述⽅式运⾏，我们可以给出⼀个貌似合理的理由去解释为什么⽤10 个输出⽽不是4 个。如果我们有4 个输出，那么第⼀个输出神经元将会尽⼒去判断数字的最⾼有效位是什么。把数字的最⾼有效位和数字的形状联系起来并不是⼀个简单的问题。很难想象出有什么恰当的历史原因，⼀个数字的形状要素会和⼀个数字的最⾼有效位有什么紧密联系。
上⾯我们说的只是⼀个启发性的⽅法。没有什么理由表明这个三层的神经⽹络必须按照我所描述的⽅式运⾏，即隐藏层是⽤来探测数字的组成形状。可能⼀个聪明的学习算法将会找到⼀些合适的权重能让我们仅仅⽤4 个输出神经元就⾏。但是这个启发性的⽅法通常很有效，它会节省你⼤量时间去设计⼀个好的神经⽹络结构。

使用梯度下降算法进行学习

首先需要数据集，称为训练数据集。这里使用的是MNIST数据集。 分为两个部分。第一部分是60000幅用于训练的图像，第二部分是10000用于测试的图像。
使用X来表示一个训练输入。为了方便，将每个训练输入X看作是一个28*28=784维的向量。每个向量的项目代表单个像素的灰度值。使用y=y(x)来表示对应的期望输出，y是一个10维的向量。
为了量化我们的目标，定义一个代价函数。如图

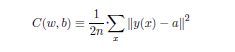
这里W是权重的集合，b是所有的偏置，n是训练输入数据的个数，a是输出的向量。
作者称其为二次代价函数， 其实就是均方误差或者MSE。
这里，我们的目标就成为了寻找最小的代价函数C.
为什么要使用C呢？作者这么解释：

这么做是因为在神经⽹络中，被正确分类的图像数量所关于权重和偏置的函数并不是⼀个平滑的函数。⼤多数情况下，对权重和偏置做出的微⼩变动完全不会影响被正确分类的图像的数量。这会导致我们很难去解决如何改变权重和偏置来取得改进的性能。⽽⽤⼀个类似⼆次代价的平滑代价函数则能更好地去解决如何⽤权重和偏置中的微⼩的改变来取得更好的效果

然后我们把这个问题简化为一个最小化一个给定的多元函数上来。 所以我们选择使用一种梯度下降的技术。

实现网络

当然，第一是下载数据。MNIST数据是60000个训练数据加上10000测试数据。我们进行了调整。用50000数据验证呢个，然后预留一个单独的10000个图像的验证集，作用日后再说。
当然，还需要安装Numpy.

在列出完整代码前，先解释一下核心特性。核心片段是一个Network类，用来表示一个神经网络。这是用来初始化Network对象的代码：

class Network(object)
    def __init__(self,sizes):
    self.num_layers = len(sizes)
    self.sizes = sizes
    self.biases = [np.random.randn(y,1) for y in sizes[1:]]
    self.weights = [np.random.randn(y,x) for x,y in zip(sizes[:-1],sizes[1:])]

在这段代码里，列表sizes包含各层神经元的数量。例如，如果我们想创建一个在第一层有2个，第二层有3个，最后层有1个神经元的对象，代码应该写：

net=Network([2,3,1])

Network对象中的偏置和权重都是被随机初始化的，使用Numpy的np.random.randn函数来生成均值为0，标准差为1的高斯分布。这样的随机初始化给了我们的随机梯度下降算法一个起点。
另外，偏置和权重以Numpy矩阵列表的形式存储。例如，net.weights[1]是一个存储着连接第二层和第三层神经元权重的Numpy矩阵。

有了这些，很容易写出从一个Network实例计算输出的代码我们从定义S型函数开始：

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

当输入z是一个向量或者Numpy数组是，Numpy自动按元素应用sigmoid函数。
然后添加一个feedforward方法，对于给定的输入a，返回对应的输出。

def feedforward(self,a):
    for b,w in zip(self.biases,self.weights):
        a=sigmiod(np.dot(w,a)+b)
    return a

当然，我们想要Network所做的主要工作就是学习。为此我们添加一个实现随机梯度下降的SGD方法。

def SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None):
    if test_data:n_test = len(test_data)
    n= len(training_data)
    for j in xrange(epochs)
        random.shuffle(training_data)
        mini_batches=[training_data[k:k+mini_batch_size]
        for k in xrange(0,n,mini_batch_size)
    for mini_batch in mini_batches:
        self.update_mini_batch(mini_batch,eta)
    if test_data:
        print "Epoch {0};{1}/{2}".format(j,self.evaluate(test_data),n_test)
    else:
        print "Epoch {0} complete".format(j)

training_data 是一个（x,y）元组的列表，表示训练输入和其对应的期望输出。变量epochs 和 mini_batch_size是迭代期变量和采样时小批量数据 的大小。eta是学习速率。如果给定了可选参数test_data，那么程序会在训练器后评估网络，并打印进展，但会拖慢速度。
代码在每个迭代期，首先随机的将训练数据打乱，然后将他分为多个适当大小的小批量数据。然后对于每一个mini_batch，我们应用一次梯度下降。这是通过self.update_mini_batch(mini_batch,eta)完成的。他仅仅使用mini_batch中的训练数据，根据单次梯度下降的迭代更新网络的权重和偏置。

def update_mini_batch(self,mini_batch,eta):
    nabla_b=[np.zeros(b.shape) for b in self.biases]
    nabla_w=[np.zeros(w.shape) for w in self.weights]
    for x,y in mini_batch:
        delta_nabla_b,delta_nabla_w = self.backprop(x,y)
        nabla_b = [nb+dnb for nb,dnb in zip(nabla_b,delta_nabla_b)]
        nabla_w = [nw+dnw for nw,dnw in zip(nabla_w,delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch)*nw for w,nw in zip(self.weights,nabla_w)]
        self.biases = [b-(eta/len(mini_batch)*nb for b,nb in zip(self.biases,nabla_b)]

大部分工作由delta_nabla_b,delta_nabla_w = self.backprop(x,y)完成。
这里调用了反向传播的算法。一种快速计算代价函数的梯度的算法。因此上述函数仅仅是对mini_batch中的每一个训练样本计算梯度，然后适当的更新self.weights和self.biases。

完整的代码如下：

"""
network.py
~~~~~~~~~~

一种实现随机梯度下降学习算法的前馈神经网络模块。 使用反向传播计算梯度。 注意，作者专注于使代码简单，易于阅读，并且容易修改。 它没有被优化，并且省略了许多期望的特征。
"""

#### Libraries
# Standard library
import random

# Third-party libraries
import numpy as np

class Network(object):

    def __init__(self, sizes):
        """列表“sizes”包含网络各层中的神经元数量。 使用具有均值0和方差1的高斯分布来随机地初始化网络的偏差和权重。注意，第一层被假定为输入层，并且按照惯例，我们将不为这些神经元设置任何偏差， 因为偏差只用于计算来自后续层的输出。"""
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]

    def feedforward(self, a):
        """如果输入“a”，则返回网络的输出。"""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """使用随机梯度下降训练神经网络。 ``training_data``是一个表示训练输入和所需输出的元组“（x，y）”的列表。 其他非可选参数是不言自明的。 如果提供了``test_data``，那么网络将在每个迭代之后针对测试数据进行评估，并且打印出来。 这对于跟踪进度很有用，但会大大减慢速度。"""
        if test_data: n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(
                    j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)

    def update_mini_batch(self, mini_batch, eta):
        """通过对单个迭代单元使用反向传播应用梯度下降来更新网络的权重和偏差。
         ``mini_batch``是元组“`（x，y）``的列表，`eta``是学习率。"""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        """返回表示成本函数C_x的梯度的元组“`（nabla_b，nabla_w）``。 “nabla_b”和“nabla_w”是numpy数组的逐层列表，类似于“self.biases”和“self.weights”。"""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def evaluate(self, test_data):
        """返回神经网络输出正确结果的测试输入数。 注意，神经网络的输出被假定为最终层中具有最高激活的任何神经元的指数。"""
        test_results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)

    def cost_derivative(self, output_activations, y):
        """返回偏导数的向量\ partial C_x / \ partial a用于输出激活。"""
        return (output_activations-y)

#### Miscellaneous functions
def sigmoid(z):
    """S函数"""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """sigmoid函数的导数。"""
    return sigmoid(z)*(1-sigmoid(z))

为验证这个程序的效果，我们先加载MNIST数据

"""
mnist_loader
~~~~~~~~~~~~
用于加载MNIST图像数据的库。 有关返回的数据结构的详细信息，请参阅“load_data”和“load_data_wrapper”的doc字符串。 在实践中，``load_data_wrapper``是通常由神经网络代码调用的函数。
"""

#### Libraries
# Standard library
import cPickle
import gzip

# Third-party libraries
import numpy as np

def load_data():
    """将MNIST数据作为包含训练数据，验证数据和测试数据的元组返回。
``training_data``作为一个具有两个条目的元组返回。
     第一个条目包含实际的训练图像。 这是一个numpy ndarray有50,000个条目。 每个条目又是具有784个值的numpy ndarray，表示单个MNIST图像中的28 * 28 = 784个像素。

     ``training_data``元组中的第二个条目是一个numpy ndarray，包含50,000个条目。 这些条目仅是包含在元组的第一条目中的相应图像的数字值（0 ... 9）。

     “validation_data”和“test_data”是相似的，除了每个只包含10,000个图像。

     这是一个很好的数据格式，但是对于在神经网络中使用有帮助的是，稍微修改``training_data``的格式。 这在包装函数“load_data_wrapper（）”中完成，见下文。
    """
    f = gzip.open('../data/mnist.pkl.gz', 'rb')
    training_data, validation_data, test_data = cPickle.load(f)
    f.close()
    return (training_data, validation_data, test_data)

def load_data_wrapper():
    """返回一个包含``（training_data，validation_data，test_data）`的元组。 基于``load_data``，但是这种格式在我们的神经网络实现中更方便。

    特别是，``training_data``是一个包含50,000个2元组“（x，y）”的列表。 ``x``是一个包含输入图像的784维numpy.ndarray。 ``y``是一个10维的numpy.ndarray，表示对应于``x``的正确数字的单位向量。

    “validation_data”和“test_data”是包含10,000个2元组“（x，y）”的列表。 在每种情况下，``x``是一个包含输入图像的784维numpy.ndarry，``y``是相应的分类，即对应于``x``的数字值（整数）。

     显然，这意味着我们对训练数据和验证/测试数据使用稍微不同的格式。 这些格式证明是最方便的在我们的神经网络代码中使用。"""
    tr_d, va_d, te_d = load_data()
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    training_data = zip(training_inputs, training_results)
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    validation_data = zip(validation_inputs, va_d[1])
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    test_data = zip(test_inputs, te_d[1])
    return (training_data, validation_data, test_data)

def vectorized_result(j):
    """返回一个10维的单位向量，在第j个位置为1.0，在其他位置为零。 这用于将数字（0 ... 9）转换成来自神经网络的对应的期望输出。"""
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

在Python shell中执行以下的指令，加载MNIST数据

>>>import mnist_loader
>>>training_data,validation_data,test_data = mnist_loader.load_data_wrapper()

加载完成之后，设计一个Network.

>>>improt Network
>>>net = network.Network([784,30,10])

最后，使用随机梯度下降来从mnist数据学习超过30次迭代期，小批量数据大小为10，学习速率为3.0，

>>>net.SGD(training_data,30,10,3.0,test_data=test_data)

这样就可以等待程序结果了。因为我们开始是随机的，所以每次运行的结果不会相同。
而且，我们可以通过通过改进隐含层神经元数量来改进程序。使用更多的神经元可能会获得更好的结果，但是这不是绝对的。

我们不得不对训练的迭代期数量，小批量数据大小和学习速率做特别的选择，这些参数被称为超参数。
上文我们把学习速率选择了3.0，如果是0.001的话，效果会非常的不理想，但是网络的性能会随着时间的推移慢慢的变好。
但是学习速率太高时，结果会越来越差。

如果我们第一次遇到网络效果很差的问题时，我们就应该考虑是否用了让网络很难学习的初始权重和偏置？是否没有足够的训练数据？是否没有进行足够的迭代期？学习速率是否太高或者太低？对于这样的网络，识别手写数字是不是不可能？

教训是调试一个神经网络不是琐碎的，而是一门艺术，我们需要学习更好的艺术来使神经网络获得更好的结果。更普遍的是，我们需要启发式的方法来选择超参数和好的结构。

什么是好

对比一些普通的基线。如随机猜数字，识别正确率是10%，根据灰度的话，可以达到22.25%，可以试着编写一下这个程序。
当然有很多被认可的机器学习方法，作者介绍了支持向量机，SVM。作者使用了scikit-learn Python程序库，它提供了一个简单的Python接口，包装了一个LIBSVM的C库。使用默认的设置，识别率可以达到94.35%。改善默认情况，Andreas Muller可以将SVM的识别率提高到98.5%。
当然，神经网络最厉害，最高纪录是99.79%。当然，这些科学家运用的方法依然很简单。所以：

复杂的算法<简单的算法+好的训练数据

迈向深度学习

如何理解神经网络的工作呢？假设我们要确定一幅图像是否显示有人脸，那么我们的思路：

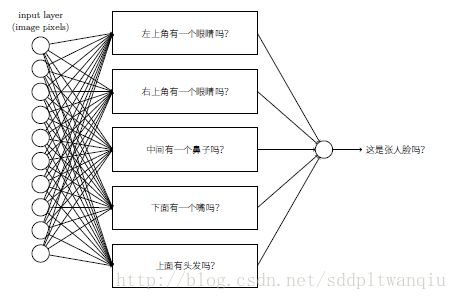
⼦⽹络也可以被继续分解

这些⼦问题也同样可以继续被分解，并通过多个⽹络层传递得越来越远。最终，我们的⼦⽹络可以回答那些只包含若⼲个像素点的简单问题。
最终的结果是，我们设计出了⼀个⽹络，它将⼀个⾮常复杂的问题——这张图像是否有⼀张⼈脸——分解成在单像素层⾯上就可回答的⾮常简单的问题。它通过⼀系列多层结构来完成，在前⾯的⽹络层，它回答关于输⼊图像⾮常简单明确的问题，在后⾯的⽹络层，它建⽴了⼀个更加复杂和抽象的层级结构。包含这种多层结构——两层或更多隐藏层——的⽹络被称为深度神经⽹络。
当然，⼿⼯设计⽹络中的权重和偏置⽆疑是不切实际的。取⽽代之的是，我们希望使⽤学习算法来让⽹络能够⾃动从训练数据中学习权重和偏差——这样，形成⼀个概念的层次结构。⾃2006 年以来，⼈们已经开发了⼀系列技术使深度神经⽹络能够学习。这些深度学习技术基于随机梯度下降和反向传播，并引进了新的想法。这些技术已经使更深（更⼤）的⽹络能够被训练——现在训练⼀个有5 到10 层隐藏层的⽹络都是很常⻅的。⽽且事实证明，在许多问题上，它们⽐那些浅层神经⽹络表现的更加出⾊。