python数据结构实现(六):图及相关LeetCode题
python数据结构实现(六)
- 1. 图
- 1.1 python实现图的邻接矩阵表示方法
- 1.1.1 python实现无向无权图
- 1.1.2 python实现无向有权图
- 1.1.3 python实现有向无权图
- 1.1.3 python实现有向有权图
- 1.2 python实现图的邻接表表示方法
- 1.2.1 无向图
- 1.2.2 有向图
- 1.3 python实现图的遍历
- 1.3.1 python实现深度优先搜索
- 1.3.2 python实现广度优先搜索
- 1.4 python实现 Dijkstra 算法
- 1.5 python实现拓扑排序
- 1.5.1 python实现拓扑排序—Kahn 算法
- 1.5.2 python实现拓扑排序—DFS 算法
- 2. LeetCode相关练习题
- 2.1 Number of Islands(岛屿的个数)(python)
- 2.2 Valid Sudoku(有效的数独)(python)
1. 图
1.1 python实现图的邻接矩阵表示方法
1.1.1 python实现无向无权图
- 通过传入一个二维数组确立邻接矩阵,无向无权图的邻接矩阵元素为0和1;
- adjMatrix[ i ][ j ] = 0 说明顶点i和j不连接,若为1则说明连接;
- 无向图的邻接矩阵总是为对称矩阵
import numpy as np
class MatrixGraph:
'''
无向图的邻接矩阵表示(为对称矩阵)
用矩阵存储顶点间的关系:顶点a与顶点b相连,则adjMatrix[vex2num[a],vex2num[b]]
的值为1,否则为0
vex2num为字典,将顶点映射为矩阵的编号
'''
def __init__(self,vertex=[]):
'''
根据传入的顶点信息表建造邻接矩阵和顶点字典
:param vertex:无向图的所有顶点组成的列表
'''
self.vexNum = len(vertex)
self.adjMatrix = np.zeros((self.vexNum,self.vexNum))
self.vex2num = {}
for index, vertex in enumerate(vertex):
self.vex2num[vertex] = index
def createGraph(self, maxtrix):
'''
传入一个矩阵确立顶点间的关系
'''
if maxtrix.shape == self.adjMatrix.shape:
self.adjMatrix = maxtrix
else:
raise Exception('wrong matrix shape')
def isLinked(self, vex1, vex2):
# 判断图中两个顶点是否连接
return self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] == 1
def linkVex(self, vex1, vex2):
# 连接无向图的两个顶点
if vex1 != vex2:
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = 1
self.adjMatrix[self.vex2num[vex2], self.vex2num[vex1]] = 1
def splitVex(self, vex1, vex2):
# 断开无向图的两个顶点
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = 0
self.adjMatrix[self.vex2num[vex2], self.vex2num[vex1]] = 0
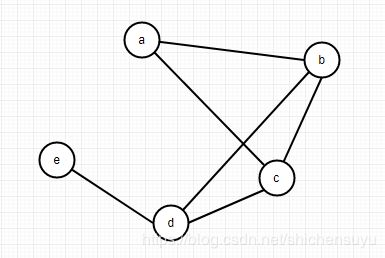
生成无向无权图:
vexs = ['a','b','c','d','e']
Mgraph = MatrixGraph(vexs)
matrix = np.array([[0,1,1,0,0],[1,0,1,1,0],\
[1,1,0,1,0],[0,1,1,0,1],[0,0,0,1,0]])
Mgraph.createGraph(matrix)
print(Mgraph.adjMatrix)
Mgraph.isLinked('a','d')
=====================================
[[0 1 1 0 0]
[1 0 1 1 0]
[1 1 0 1 0]
[0 1 1 0 1]
[0 0 0 1 0]]
False
1.1.2 python实现无向有权图
- 无向有权图与无向无权图的区别仅在与邻接矩阵中的元素
- adjMatrix[i][j] 为路权大小则说明顶点i和j相连;若为inf则说明两个顶点间没有直接路径,即不相连
import numpy as np
inf = float('inf')
class MatrixGraph:
'''
无向有权图的邻接矩阵表示(为对称矩阵)
用矩阵存储顶点间的关系:顶点a与顶点b相连,则adjMatrix[vex2num[a],vex2num[b]]的值为路权,否则为inf
vex2num为字典,将顶点映射为矩阵的编号
'''
def __init__(self,vertex=[]):
'''
根据传入的顶点信息表建造邻接矩阵和顶点字典
:param vertex:无向图的所有顶点组成的列表
'''
self.vex2num = {}
self.vexNum = len(vertex)
self.adjMatrix = np.array([[inf]*self.vexNum]*self.vexNum)
for index, vertex in enumerate(vertex):
self.vex2num[vertex] = index
def createGraph(self, maxtrix):
'''
传入一个带权矩阵确立顶点间的关系
'''
if maxtrix.shape == self.adjMatrix.shape:
self.adjMatrix = maxtrix
else:
raise Exception('wrong matrix shape')
def isLinked(self, vex1, vex2):
return not self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] == inf
def linkVex(self, vex1, vex2, weight):
# 连接无向图的两个顶点
if vex1 != vex2:
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = weight
self.adjMatrix[self.vex2num[vex2], self.vex2num[vex1]] = weight
def splitVex(self, vex1, vex2):
# 断开无向图的两个顶点
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = inf
self.adjMatrix[self.vex2num[vex2], self.vex2num[vex1]] = inf
生成无向有权图:
vexs = ['a','b','c','d','e']
Mgraph = MatrixGraph(vexs)
matrix = np.array([[inf,9,12,inf,9],[9,inf,7,10,inf],[12,7,inf,3,inf],\
[inf,10,3,inf,14],[9,inf,inf,14,inf]])
Mgraph.createGraph(matrix)
print(Mgraph.adjMatrix)
print(Mgraph.isLinked('a','d'))
Mgraph.linkVex('a','d', 11)
print(Mgraph.adjMatrix)
print(Mgraph.isLinked('a','d'))
=================================
[[inf 9. 12. inf 9.]
[ 9. inf 7. 10. inf]
[12. 7. inf 3. inf]
[inf 10. 3. inf 14.]
[ 9. inf inf 14. inf]]
False
[[inf 9. 12. 11. 9.]
[ 9. inf 7. 10. inf]
[12. 7. inf 3. inf]
[11. 10. 3. inf 14.]
[ 9. inf inf 14. inf]]
True
1.1.3 python实现有向无权图
import numpy as np
class MatrixOrientedGraph:
'''
有向图的邻接矩阵表示
用矩阵存储顶点间的关系:顶点a指向顶点b,则adjMatrix[vex2num[a],vex2num[b]]的值为1,否则为0
vex2num为字典,将顶点映射为矩阵的编号
'''
def __init__(self,vertex=[]):
'''
根据传入的顶点信息表建造邻接矩阵和顶点字典
:param vertex:有向图的所有顶点组成的列表
'''
self.vertexNum = len(vertex)
self.adjMatrix = np.zeros((self.vertexNum,self.vertexNum))
self.vex2num = {}
for index, vertex in enumerate(vertex):
self.vex2num[vertex] = index
def createGraph(self, maxtrix):
'''
传入一个矩阵确立顶点间的关系
'''
if maxtrix.shape == self.adjMatrix.shape:
self.adjMatrix = maxtrix
else:
raise Exception('wrong matrix shape')
def isLinked(self, vex1, vex2):
return self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] == 1
def linkVex(self, vex1, vex2):
# 连接有向图的两个顶点
if vex1 != vex2:
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = 1
def splitVex(self, vex1, vex2):
# 断开有向图的两个顶点
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = 0
生成有向图:
vexs = ['a','b','c','d','e']
Mgraph = MatrixOrientedGraph(vexs)
matrix = np.array([[0,1,0,0,1],[0,0,0,1,0],[0,1,0,0,0],\
[0,0,0,0,0],[0,0,1,0,0]])
Mgraph.createGraph(matrix)
print(Mgraph.adjMatrix)
Mgraph.isLinked('a','d')
============================
[[0 1 0 0 1]
[0 0 0 1 0]
[0 1 0 0 0]
[0 0 0 0 0]
[0 0 1 0 0]]
False
1.1.3 python实现有向有权图
import numpy as np
inf = float('inf')
class MatrixOrientedGraph:
'''
有向有权图的邻接矩阵表示
用矩阵存储顶点间的关系:顶点a指向顶点b,则adjMatrix[vex2num[a],vex2num[b]]的值为路权,否则为inf
vex2num为字典,将顶点映射为矩阵的编号
'''
def __init__(self,vertex=[]):
'''
根据传入的顶点信息表建造邻接矩阵和顶点字典
:param vertex:无向图的所有顶点组成的列表
'''
self.vertexNum = len(vertex)
self.adjMatrix = np.zeros((self.vertexNum,self.vertexNum))
self.vex2num = {}
for index, vertex in enumerate(vertex):
self.vex2num[vertex] = index
def createGraph(self, maxtrix):
'''
传入一个矩阵确立顶点间的关系
'''
if maxtrix.shape == self.adjMatrix.shape:
self.adjMatrix = maxtrix
else:
raise Exception('wrong matrix shape')
def isLinked(self, vex1, vex2):
return not self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] == inf
def linkVex(self, vex1, vex2, weight):
# 连接有向图的两个顶点,weight为两点的路权
if vex1 != vex2:
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = weight
def splitVex(self, vex1, vex2):
# 断开无向图的两个顶点
self.adjMatrix[self.vex2num[vex1], self.vex2num[vex2]] = inf
生成有向有权图:
vexs = ['a','b','c','d','e','g','f']
Mgraph = MatrixGraph(vexs)
matrix = np.array([[inf,4,6,6,inf,inf,inf],[inf,inf,1,inf,7,inf,inf],\
[inf,inf,inf,inf,6,4,inf],[inf,inf,2,inf,inf,5,inf],\
[inf,inf,inf,inf,inf,inf,6],[inf,inf,inf,inf,1,inf,8],\
[inf,inf,inf,inf,inf,inf,inf]])
Mgraph.createGraph(matrix)
print(Mgraph.adjMatrix)
Mgraph.isLinked('a','d')
================================
[[inf 4. 6. 6. inf inf inf]
[inf inf 1. inf 7. inf inf]
[inf inf inf inf 6. 4. inf]
[inf inf 2. inf inf 5. inf]
[inf inf inf inf inf inf 6.]
[inf inf inf inf 1. inf 8.]
[inf inf inf inf inf inf inf]]
1.2 python实现图的邻接表表示方法
1.2.1 无向图
class ArcNode:
def __init__(self, adjvex=None, nextarc=None):
'''
初始化边表结点
:param adjvex:该弧所指向的顶点的位置
:param nextarc:指向下一条弧的指针
'''
self.adjvex = adjvex
self.nextarc = nextarc
class VNode:
def __init__(self, no, firstarc=None):
'''
初始化顶点表
:param no:顶点信息
:param firstarc:指向第一条依附该顶点的弧的指针
'''
self.no = no
self.firstarc = firstarc
class ALGraph:
def __init__(self, vertexs):
self.vexNum = len(vertexs)
self.adjlist = [0] * self.vexNum
def create(self, vex1, vexs=[]):
'''
生成顶点vex1的邻接表结构
:param vex1:顶点
:param vexs:与顶点vex1相连的其他顶点
'''
self.adjlist[vex1] = VNode(vex1)
arcnode = ArcNode(vexs[0])
self.adjlist[vex1].firstarc = arcnode
p = self.adjlist[vex1].firstarc
for vex in vexs[1:]:
arcnode = ArcNode(vex)
p.nextarc = arcnode
p = p.nextarc
def showALGraph(self):
for vex in range(self.vexNum):
print('与顶点%d相连接的顶点有:'%vex)
p = self.adjlist[vex].firstarc
while p:
print(p.adjvex,end=' ')
p = p.nextarc
print('\n')
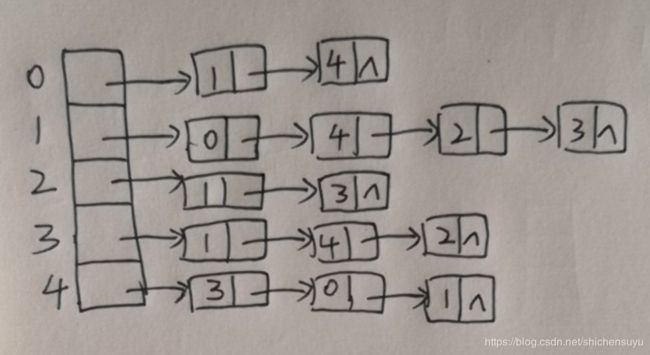
生成无向图:
algraph = ALGraph([0,1,2,3,4])
algraph.create(0,[1,4])
algraph.create(1,[0,4,2,3])
algraph.create(2,[1,3])
algraph.create(3,[1,4,2])
algraph.create(4,[3,0,1])
algraph.showALGraph()
===========================
与顶点0相连接的顶点有:
1 4
与顶点1相连接的顶点有:
0 4 2 3
与顶点2相连接的顶点有:
1 3
与顶点3相连接的顶点有:
1 4 2
与顶点4相连接的顶点有:
3 0 1
1.2.2 有向图
无向图与有向图的邻接表表示法差别在于:
无向图:若a与b相连接,则顶点a可以遍历到顶点b,顶点b可以遍历到顶点a,故无向图的邻接表中边结点会出现两次
有向图:若a指向b,而b不指向a,则在顶点a开始遍历能遍历到b结点,而在顶点b开始遍历则不会遍历到顶点a,故有向图边结点只出现一次
即:有向图的邻接表表示方法与无向图的一样,只是传入连接数据构成邻接表时注意连接方向即可
1.3 python实现图的遍历
1.3.1 python实现深度优先搜索
visited = [False] * algraph.vexNum # 访问数组,algraph为待遍历的图
def visit(vex):
# 访问顶点的函数,这里只做了简单的打印
print(vex,end=' ')
def DFS(graph,v):
# 基于邻接表表示的深度优先遍历,从顶点v开始遍历整个图
visit(v)
visited[v] = True
p = graph.adjlist[v].firstarc
while p:
if visited[p.adjvex] == False:
return DFS(graph, p.adjvex)
p = p.nextarc
遍历1.2.1邻接表表示的无向图:
DFS(algraph, 3) # 从顶点3开始进行深度优先遍历
==============================
3 1 0 4
1.3.2 python实现广度优先搜索
图的广度优先遍历类似于树的层次遍历,这里也借助了队列存储结点
import queue
que = queue.Queue(algraph.vexNum) # algraph为待遍历的图
visited = [False] * algraph.vexNum
def visit(vex):
# 访问顶点的函数
print(vex,end=' ')
def BFS(graph, v):
# 基于邻接表的广度优先遍历,从顶点v开始遍历整个图
visit(v)
visited[v] = True
que.put(v)
while not que.empty():
vex = que.get()
p = graph.adjlist[vex].firstarc
while p:
if not visited[p.adjvex]:
visit(p.adjvex)
visited[p.adjvex] = True
que.put(p.adjvex)
p = p.nextarc
遍历1.2.1邻接表表示的无向图:
BFS(algraph, 2) # 从顶点2开始广度优先遍历该图
===============================
2 1 3 0 4
1.4 python实现 Dijkstra 算法
Dijkstra算法用于求单源最短路径,即求图中一顶点v到其余各顶点的最短路径
需要设置三个辅助数组:
1.dist[vi]:表示当前已找到的顶点v到顶点vi的最短路径长度;
初始化dist数组时,若v与vi之间有直接路径,则dist[vi]标为对应路权;若v与vi之间没有直接路径,则dist[vi]标为inf
2.path[vi]:表示顶点v到顶点vi的路径上vi的前一个顶点;最终结果的最短路径存储在path数组中
初始化path数组时,若v与vi之间有直接路径,则path[vi]标为v;若v与vi之间没有直接路径,则path[vi]标为-1
3.set数组:set数组作为标记数组,若set[vi]==1,则表明vi已被并入最短路径中
初始化set数组时,set[v]=1,其余标为0
'''
算法的基本思想:基于贪心策略,从起始顶点v开始,选择v到其余顶点的直接路径中
最小的一条的顶点vi并入到set中,更新path数组和set数组,
并以vi为中转点修改v经过vi到其余顶点的最短路径,即更新dist数组,
重复该操作vexNum-1次,使得所有顶点都被并入最短路径
'''
inf = float('inf')
def Dijkstra(graph, v):
# graph为邻接矩阵表示的图,算法求得顶点v到其余顶点的最短路径
set = [0] * graph.vexNum; set[v] = 1
path = [-1] * graph.vexNum
dist = [inf] * graph.vexNum
dist[v] = 0
for vex,value in enumerate(graph.adjMatrix[v]):
if value != inf:
dist[vex] = value
path[vex] = v
for _ in range(graph.vexNum-1):
# 遍历graph.vexNum-1次,使得所有顶点都并入到最短路径中
min = inf
for index, distance in enumerate(dist):
# 求出当前v到dist数组中未并入最短路径的顶点的最短路径
if set[index] == 0 and distance < min:
min = distance; indexMin = index
set[indexMin] = 1
for otherVex in range(graph.vexNum):
if set[otherVex] == 0 and dist[indexMin] \
+ graph.adjMatrix[indexMin][otherVex] < dist[otherVex]:
dist[otherVex] = dist[indexMin] \
+ graph.adjMatrix[indexMin][otherVex]
path[otherVex] = indexMin
return path,dist
def printPath(path, targetVex):
# 打印到顶点targetVex的最短路径
stack = []
while path[targetVex] != -1:
stack.append(targetVex)
targetVex = path[targetVex]
stack.append(targetVex)
while stack:
vex = stack.pop()
print(vex,end='-->')
用Dijkstra算法求出1.1.3的图从0到其他顶点的最短路径

path,dist = Dijkstra(Mgraph, 0)
printPath(path,4) # 打印出顶点0到顶点4的最短路径
print(dist[4]) # 打印出顶点0到顶点4的最短路径长度
===============================
0-->1-->2-->5-->4-->
10.0
1.5 python实现拓扑排序
1.5.1 python实现拓扑排序—Kahn 算法
算法基本思想:
- 设置一个栈stack用于记录当前图中入度为0的顶点
- 设置一个记录已经放入结果集re的顶点个数的计数器count(用于比较满足拓扑排序的顶点个数和图的顶点个数,若相等则说明该图满足拓扑排序的要求,即为有向无环图),初始为0
- 将所有入度为0的顶点入栈,当栈不空时执行以下循环
\qquad (1) 出栈,将顶点放入结果集re,计数器加1
\qquad (2) 将由此顶点引出的边所指向的所有顶点的入度减一,若刚好变为入度为0的顶点则令其入栈
def KahnTopologicalSort(algraph, indegrees):
# indegrees为各个顶点的入度,图中顶点从0开始编号
stack = []; re = []
count = 0 # 计数器用于统计加入结果列表re的顶点数
for vex in algraph.adjlist:
if indegrees[vex.no] == 0:
stack.append(vex)
while stack:
vnode = stack.pop()
p = vnode.firstarc
count += 1
re.append(vnode.no)
while p:
if p.adjvex:
indegrees[p.adjvex] -= 1
if indegrees[p.adjvex] == 0:
stack.append(algraph.adjlist[p.adjvex])
p = p.nextarc
else:
break
if count == algraph.vexNum:
print('TopologicalSort succeeds!')
return re
else:
print('TopologicalSort fails!The graph is not qualified!')
return False
class ArcNode:
def __init__(self, adjvex=None, nextarc=None):
'''
初始化边表结点
:param adjvex:该弧所指向的顶点的位置
:param nextarc:指向下一条弧的指针
'''
self.adjvex = adjvex
self.nextarc = nextarc
class VNode:
def __init__(self, no, firstarc=None):
'''
初始化顶点表
:param no:顶点信息
:param firstarc:指向第一条依附该顶点的弧的指针
'''
self.no = no
self.firstarc = firstarc
class ALGraph:
def __init__(self, vertexs):
self.vexNum = len(vertexs)
self.adjlist = [0] * self.vexNum
def create(self, vex1, vexs=[]):
'''
生成顶点vex1的邻接表结构
:param vex1:顶点
:param vexs:与顶点vex1相连的其他顶点
'''
self.adjlist[vex1] = VNode(vex1)
arcnode = ArcNode(vexs[0])
self.adjlist[vex1].firstarc = arcnode
p = self.adjlist[vex1].firstarc
for vex in vexs[1:]:
arcnode = ArcNode(vex)
p.nextarc = arcnode
p = p.nextarc
def showALGraph(self):
for vex in range(self.vexNum):
print('与顶点%d相连接的顶点有:'%vex)
p = self.adjlist[vex].firstarc
while p:
print(p.adjvex,end=' ')
p = p.nextarc
print('\n')
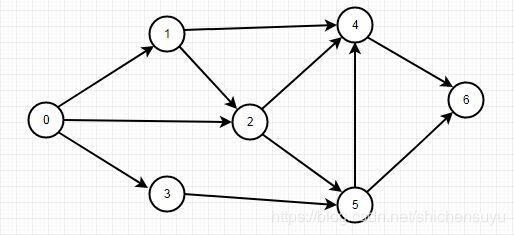
algraph = ALGraph([0,1,2,3,4,5,6])
algraph.create(0,[1,2,3])
algraph.create(1,[2,4])
algraph.create(2,[4,5])
algraph.create(3,[5])
algraph.create(4,[6])
algraph.create(5,[4,6])
algraph.create(6,[None])
result = KahnTopologicalSort(algraph, [0,1,2,1,3,2,2])
print(result)
==============================
TopologicalSort succeeds!
[0, 3, 1, 2, 5, 4, 6]
1.5.2 python实现拓扑排序—DFS 算法
- 利用DFS算法实现求解拓扑有序序列的前提是要求该图必须为有向无环图
- 判断该图是否为有向无环图,也可通过在深度遍历过程中去进行判定,大概思路是:从某顶点A出发的深度遍历,若在遍历过程中出现了某一条边指向了顶点A的情况,则可说明该图存在回路
'''
当有向图无环时,深度优先遍历会遍历到最后一个出度为0的顶点,
它是拓扑有序序列的最后一个顶点,将其存储到结果集中,如此递归下去,
结果集最终存储的结果即为逆拓扑有序序列,再将其反转转化为拓扑有序序列即可
'''
visited = [False] * algraph.vexNum
re = []
def DFSTopSort(algraph, v):
visited[v] = True
p = algraph.adjlist[v].firstarc
while p and p.adjvex:
if not visited[p.adjvex]:
DFSTopSort(algraph, p.adjvex)
p = p.nextarc
re.append(v) # 在递归返回前将出弹出系统栈的顶点保存到结果集re
对该算法求出上图的拓扑排序序列:
DFSTopSort(algraph, 0)
re[::-1] # 函数处理后的re为逆拓扑有序序列,需将其反转为拓扑有序序列
================================
[0, 3, 1, 2, 5, 4, 6]
2. LeetCode相关练习题
2.1 Number of Islands(岛屿的个数)(python)
采用深度优先遍历的方法构建一个沉没相邻岛屿的函数,在发现岛屿时递归调用沉没函数,则发现岛屿的次数即为岛屿的个数
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
re = 0
if grid:
height = len(grid)
width = len(grid[0])
def sink(i, j):
nonlocal height,width
if 0 <= i < height and 0 <= j < width and int(grid[i][j]):
grid[i][j] = '0'
for a, b in zip([i-1,i,i+1,i],[j,j-1,j,j+1]):
sink(a, b)
for m in range(height):
for n in range(width):
if int(grid[m][n]):
re += 1
sink(m, n)
return re
2.2 Valid Sudoku(有效的数独)(python)
依次检查行,检查列,检查每个9方格
执行用时 : 64 ms, 在Valid Sudoku的Python3提交中击败了97.42% 的用户
内存消耗 : 13 MB, 在Valid Sudoku的Python3提交中击败了97.41% 的用户
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
for row in board:
lst = [value for value in row if value != '.']
if len(set(lst)) != len(lst):
return False
for n in range(9):
lst = [board[x][n] for x in range(9) if board[x][n] != '.']
if len(set(lst)) != len(lst):
return False
for row in [0,3,6]:
for col in [0,3,6]:
lst = [board[row + i][col + j] for i in range(3) for j in range(3) if board[row + i][col + j] != '.']
if len(set(lst)) != len(lst):
return False
return True