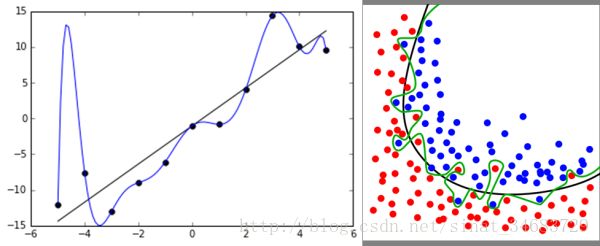
过拟合overfitting

下面左图即为欠拟合，中图为合适的拟合，右图为过拟合。 

过拟合：在模型参数拟合过程中，由于训练数据包含抽样误差，训练时复杂的模型将抽样误差也考虑在内（抽样误差也进行了拟合）。模型泛化能力弱，在训练集上效果好，在测试集上效果差。

导致过拟合的原因（包括但不限于如下几个）：

训练样本过少，不足以对整个样本空间进行分布估计;对模型进行过度训练（overtraining）

​避免过拟合的方法：early stopping、数据集扩增（Data augmentation）、正则化（Regularization）、Dropout等。

1.​early stopping

​模型训练过程中常用到迭代的思路，例如梯度下降算法。Early stopping是在迭代收敛之前，就通过一定标准提前终止迭代来防止过拟合。

具体做法是在每个​Epoch结束时（一个Epoch集为对所有的训练数据的一轮遍历），查看模型性能评价指标的变化情况，如果模型性能不再提高，就停止训练。这里的重点就是如何确认模型性能不再提高了。以准确率为例，并不是说一旦准确率发生下降就是不再提高了，因为可能经过这个Epoch后，准确率降低了，但是随后的Epoch又让准确率又上去了，所以不能根据一两次的连续降低就判断不再提高。

判断准确率是否提高的做法是，在训练过程中记录到目前为止最好的准确率，当连续10次Epoch（或若干次）​没有达到这个最佳准确率时，就认为不会再提高，停止迭代。

2.数据集增扩

​根据独立同分布假设，更多的数据往往对样本空间的整体分布估计更准确，不过实际应用中由于种种原因，并不一定总能获得足够的数据，例如成本问题。

通俗得讲，数据机扩增即需要得到更多的符合要求的数据，即和已有的数据是独立同分布的，或者近似独立同分布的。一般有以下方法：从数据源头采集更多数据；复制原有数据并加上随机噪声；重采样；根据当前数据集估计数据分布参数，使用该分布产生更多数据等。

3.正则化方法（Regularization）​、权重衰减（weight decay ）

大的权值会使得系统出现过拟合，降低其泛化性能。为了避免出现overfitting,会给误差函数添加一个惩罚项，常用的惩罚项是所有权重的平方乘以一个衰减常量之和。将权值大小加到cost里，训练时用来惩罚大的权值。训练时一方面降低输出与样本之间的误差，一方面降低权值发大小。参考自http://blog.sina.com.cn/s/blog_890c6aa30100z7su.html

​关于正则化（优化时，在目标函数或代价函数后面加上一个正则项）可以避免过拟合的原因，有如下几种角度进行解释：

1）​正则化是假设模型的参数服从先验概率，即为模型参数添加先验，不同的正则化方式的先验分布不一样（L1正则是拉普拉斯先验，而L2正则则是高斯先验）。规定了参数的分布，降低了模型的复杂度，增强对噪声和异常点的抗干扰能力。

2）​L2与L1的区别在于，L1正则是拉普拉斯先验，而L2正则则是高斯先验。它们都是服从均值为0，协方差为1/λ。当λ=0时，即没有先验。没有正则项，则相当于先验分布具有无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练集数据， 参数w可以变得任意大从而使得模型不稳定，即方差大而偏差小。λ越大，标明先验分布协方差越小，偏差越大，模型越稳定。即，加入正则项是在偏差bias与方差variance之间做平衡tradeoff。之前关于正则化介绍中有一幅图如下：

​上图中的模型是线性回归，有两个特征，要优化的参数分别是w1和w2，左图的正则化是l2，右图是l1。蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值（假设一个样本），半径就是误差值，受限条件就是红色边界（就是正则化那部分，我的理解是这个红色边界就是限定了先验分布），二者相交处，才是最优参数。可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏。

4 Dropout

这是神经网络中的一种方法，通过修改神经网络本身结构来防止过拟合。

​此外，maxout、DropConnect号称是对Dropout的改进。可参考http://www.cnblogs.com/tornadomeet/p/3430312.html

总结：

参考自：http://blog.csdn.net/heyongluoyao8/article/details/49429629

https://www.zhihu.com/question/59201590  （写的很详细，推荐细看）

转自：http://blog.sina.com.cn/s/blog_7103b28a0102wozt.html