排序算法二：快速排序算法原理以及MATLAB与Python实现

今天继续学习排序算法。今天的主角是快速排序算法。

1. 快速排序基本原理

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

该方法的基本思想是：

1．先从数列中取出一个数作为基准数。

2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

3．再对左右区间重复第二步，直到各区间只有一个数。

举例说明：

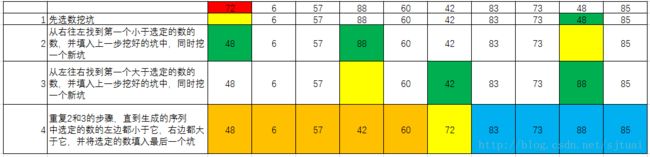
这里有一个待排序的序列：a=[72 6 57 88 60 42 83 73 48 85]

按照以上的思想，手动操作了一次这个思想：

上面的过程就是一次排序，将所有的小于选定的数全部放在了左边，全部大于选定的数放在了其右边。然后再分别对这两边的子序列进行相同的操作。知道最后需要操作的子序列中只有一个数。再排序结束。

2.MATLAB 实现

依据上面的思想对其进行代码实现。显然，对待子序列的操作最好就是使用过递归进行。

自定义快速排序函数 myQuickSort

function a=myQuickSort(a,leftIndex,rightIndex)
% a是待排序序列
%leftIndex和rightIndex是开始的左右两个边界
%%----------------------------------------------------------%%
% if leftIndex>rightIndex
%     break;
% end
if leftIndexi=leftIndex;
    j=rightIndex;
    temp=a(i);%选定的这个数挖掉，相当于挖坑
    while i<j
        while (i<j)&&(a(j)>=temp)%从右往左，找到第一个小于设定的数，
            j=j-1;
        end
        a(i)=a(j);%将找到的第一个小于设定的数填坑到最开始挖的坑里面去
        while (i<j)&&(a(i)<=temp)%从做到由，找到第一个大于选定的数
            i=i+1;
        end
        a(j)=a(i);%将找到的第一个大于选定的数填入上一步挖的坑里面去
%     if i==j
%         a(j)=temp;
%     end
    end
    a(j)=temp;%最后，i=j，将选定的数再填到上一步挖的坑里面去
    a=myQuickSort(a,leftIndex,j-1);%对左边序列进行递归
    a=myQuickSort(a,i+1,rightIndex);%对右边序列进行递归
end
end

测试函数

clc
clear
close all

a=[72 6 57 88 60 42 83 73 48 85];
leftIndex=1;
rightIndex=size(a,2);

disp('未排序的序列为：')
disp(a)

a=myQuickSort(a,leftIndex,rightIndex);

disp('快速排序之后的序列为：')
disp(a)

程序的输出为：

未排序的序列为：

    72     6    57    88    60    42    83    73    48    85

快速排序之后的序列为：

     6    42    48    57    60    72    73    83    85    88

可以看出来，效果还不错。
再换一个有相同元素的序列试试：

    72     6    57    88    60    42    83    73    48    85     6

快速排序之后的序列为：

     6     6    42    48    57    60    72    73    83    85    88

排序正确！！！

3.Python实现

#定义一个输出函数，将序列分成两部分的那个元素的索引
def findMiddleIndex(a,left,right):
    if left<right:
        i=left
        j=right
        temp=a[i]
        while iwhile iand a[j]>=temp:
                j-=1
            a[i]=a[j]
            while iand a[i]<=temp:
                i+=1
            a[j]=a[i]
        a[j]=temp
        middleIndex=i
        return middleIndex
#定义快速排序函数
def myQuickSort(a,left,right):
    if left<right:
        middleIndex=findMiddleIndex(a,left,right)
        myQuickSort(a,left,middleIndex-1)
        myQuickSort(a,middleIndex+1,right)
    return a    
#测试部分
if __name__=='__main__':
#生成随机序列
    import random
    a=[]
    aSize=a.__len__()
    while 1:
        aSize=a.__len__()
        if aSize>=20:
            break
        else:
            temp=int(random.randint(1,1000))
            a.append(temp)
    left=0
    right=a.__len__()-1
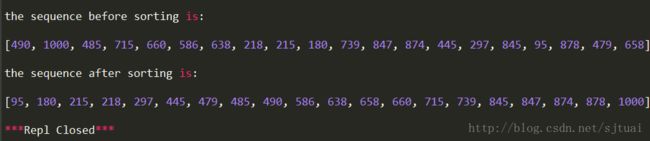
    print(myQuickSort(a,left,right))

排序正确！！！

4.快速排序算法的时间复杂度分析

已知递归算法的时间复杂度公式为： T(n)=aT[nb]+f(n)

最优时间复杂度是每次选定的数正好可以将序列分为一半，那么，就可以有：
第一次递归：

T(n)=2T[n2]+n

第二次递归： n=n2

T(n)=2{2T[n2×2]+n2}+n

=22T[n22]+2n

第三次递归： n=n2×2

T(n)=2{2{2T[n2×2×2]+n2×2}+n2}+n

=23T[n23]+3n

⋮

⋮

⋮

第 m 次递归（假定此时递归结束）： n=n2m−1

T(n)=2mT[1]+mn

也就是说：

T[n2m]=T[1]

所以有：

2m=n⇒⇒⇒m=log2n

所以，

T(n)=nT[1]+nlog2n=n+nlog2n

当 n>=2 时，

log2n>=1⇒⇒nlog1n>=n

所以其时间复杂度最终为：

T(n)=nlog2n