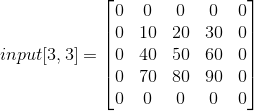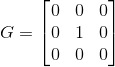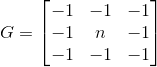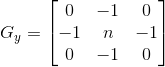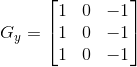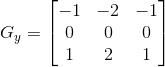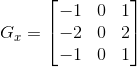OpenCV 源码详解之基本原理:卷积运算及其意义
卷积运算是如何进行的
一维卷积
定义:
![]()
理解与计算举例:
x(n)={x1, x2, x3, x4}; h(n)=(h1, h2, h3, h4);
那么:
Y(0)=x(0)h(0); //序号和=0+0=0
Y(1)=x(0)h(1)+x(1)h(0) //序号和=0+1=1+0=1
Y(2)=x(0)h(2)+x(1)h(1)+x(2)h(0); //序号和=0+2=1+2=2+0=2
Y(3)=x(0)h(3)+x(1)h(2)+x(2)h(1)+x(3)h(0); //序号和=0+3=1+2=2+1=3+0=3
Y(4)=x(0)h(4)+x(1)h(3)+x(2)h(2)+x(3)h(1) //序号和=0+4=1+3=2+2=3+1=4+0=4二维卷积
定义:
![]()
![]()
理解与计算举例:
那么:
Y(1,1)= x(0,0)h(1,1) + x(0,1)h(1,0) + x(0,2)h(1,-1) +
x(1,0)h(0,1) + x(1,1)h(0,0) + x(1,2)h(0,-1) +
x(2,0)h(-1,1) + x(2,1)h(-1,0) + x(2,2)h(-1,-1)
= x(0,0)h(1,1) + x(0,1)h(1,0) + x(1,0)h(0,1) + x(1,1)h(0,0)
Y(1,2)= x(0,0)h(1,2) + x(0,1)h(1,1) + x(0,2)h(1,0) +
x(1,0)h(0,2) + x(1,1)h(0,1) + x(1,2)h(0,0) +
Y(2,2)= x(0,0)h(2,2) + x(0,1)h(2,1) + x(0,2)h(2,0) +
x(1,0)h(1,2) + x(1,1)h(1,1) + x(1,2)h(1,0) +
x(2,0)h(0,2) + x(2,1)h(0,1) + x(2,2)h(0,0)
......
同样,可以很容易得到3维矩阵的卷积。
二维矩阵的快速计算
不过我们到这里发现,这个2维一矩阵的计算量就已经很大了,接近一个3x3的核,对一个mxn的矩阵,乘法计算量就接近9xmxn,在图像实时处理时,我们希望得到更快的处理速度。那么要如何才能实现呢?
考虑卷积的结合律性质,
![]()
我们在实际运用中,尽可能采用可分解成(ix1)*(1xj)的两个矩阵替代ixj的矩阵,
如果你直接运算,那么每个数据就会是9个乘法算,共计81次乘法(实际去掉边缘为0填充的,要少于81,但你可以先这么理解),加法运算量是8*9=72次。
![]()
如果你采用分解后的运算法,那么下面就是全部的运算量,共计6*9=54次乘法,加法运算量是4*9=36次。注意下边的*代表卷积,不是矩阵直接相乘,原文可以参考这里。
实际运算时,input会扩展成
然后进行卷积运算,如下
卷积的物理意义
本质上,对于信号处理,卷积类似是一个对周围信息的加权求和,或者说是对信号进行滤波。
定义
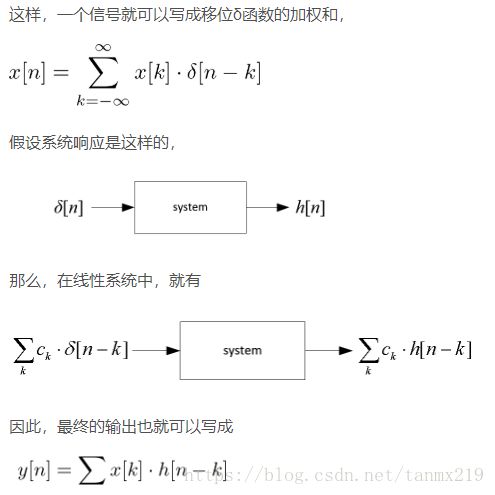
我们看一眼数学上卷积的定义(这里我们只在离散的时域中讨论),
![]()
![]()
当x[n] 是输入信号,h[n]是响应的时候,y[n]就是输出 。
为什么会是这样的呢,我们先看一下阶跃响应函数
脉冲函数的分解
在信号分解里,输入往往可以被分解成简单的输入分量。在线性系统中,输入通过系统响应后,得到的输出,也同样是各分量的组合。
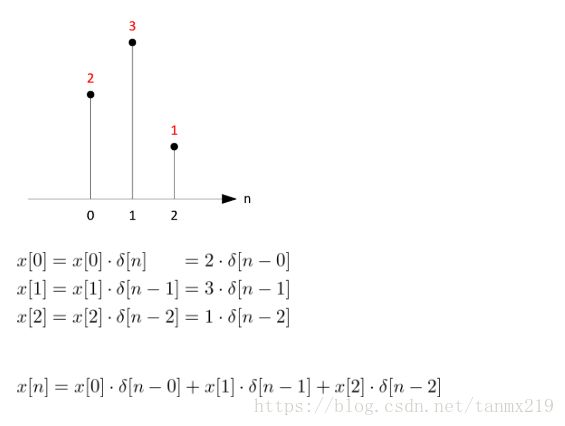
观察下面的delta函数(脉冲)输入分量,根据delta函数的性质,当n=0时,δ[n] = 1,当n ≠ 0时δ[n] = 0;这样,下图所示的输入信号 x[0]可以写成 2·δ[n],如图所示,x[0]的幅值是2;x[1]可以写成3·δ[n-1].同理,x[2]可写成 x[2] = 1·δ[n-2].
信号的响应--卷积是一个告诉你叠加效果如何的输出函数
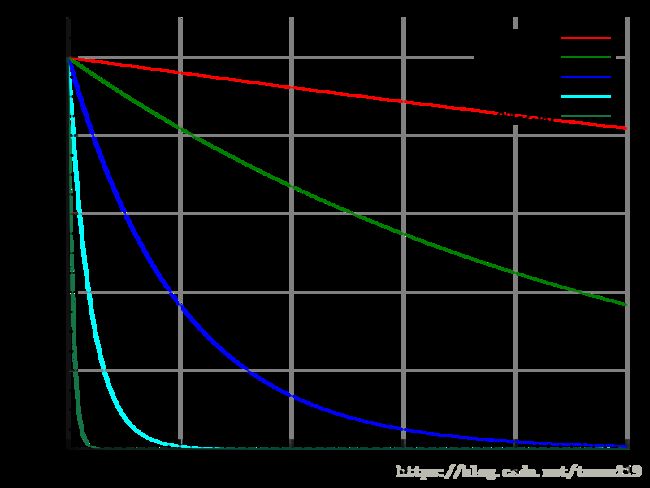
信号的响应往往具有指数衰减 Ae^(-k/T)的特性,如下图【2】
好比你用力鼓掌,鼓一下的话,过一会就不怎么疼了,也就是响应衰减了,假如你连续鼓掌,上一次鼓掌的击打效果还没消失,下一次又叠加上来,几次之后,手就会变红,也就是响应叠加了。
而卷积,正是这样一个告诉你叠加效果如何的输出函数。
几个常用的卷积的核
平滑滤波
平滑滤波的核,此时每个像素都是附近(包括自己)9个像素的平均值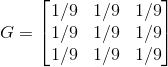
高斯平滑滤波
高斯平滑滤波的核(也叫高斯滤波,高斯模糊,高斯平滑,看一下这个矩阵,在3维空间是不是类似一个高斯分布的突起?),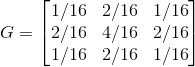
当然,你可以完全根据高斯函数![]()
自己计算出一个合适的矩阵,wikipedia(https://en.wikipedia.org/wiki/Gaussian_blur)上面计算了一个7x7的矩阵,如下
| 0.00000067 | 0.00002292 | 0.00019117 | 0.00038771 | 0.00019117 | 0.00002292 | 0.00000067 |
| 0.00002292 | 0.00078633 | 0.00655965 | 0.01330373 | 0.00655965 | 0.00078633 | 0.00002292 |
| 0.00019117 | 0.00655965 | 0.05472157 | 0.11098164 | 0.05472157 | 0.00655965 | 0.00019117 |
| 0.00038771 | 0.01330373 | 0.11098164 | 0.22508352 | 0.11098164 | 0.01330373 | 0.00038771 |
| 0.00019117 | 0.00655965 | 0.05472157 | 0.11098164 | 0.05472157 | 0.00655965 | 0.00019117 |
| 0.00002292 | 0.00078633 | 0.00655965 | 0.01330373 | 0.00655965 | 0.00078633 | 0.00002292 |
| 0.00000067 | 0.00002292 | 0.00019117 | 0.00038771 | 0.00019117 | 0.00002292 | 0.00000067 |
图像的锐化
很多资料把这个算作laplace算子(把符号反过来就是数学上推导的结果)。这个可以和下面的laplacian锐化对比看。好奇为什么叫laplace算子的可以参考:http://fourier.eng.hmc.edu/e161/lectures/gradient/node7.html,这里有详细的推导过程。
参数n是图像的锐化强度,可取任意值,越大锐化效果越明显
说明:取个n=10例子,假如一幅全灰色图,每个像素点的值都是10,中间只有一个像素点的值是11。那么处理所有其他像素点时,最大权重都是10*n=100,即使旁边那个像素值是11,也就是11-10=1的差值,基本和周围的没什么差别;但当处理到值为11的像素点时,最大权重者是11*n=110,这个对比度一下子就扩大到了10。同样的道理,假设这个点的值是12,那对比度就会扩大成20。因为图像的边缘比周围像素的对比度更高,所以通过扩大差值的方法,实现了锐化。
示例图片来自OpenCV上的例子
Perwitt梯度
如果你不嫌计算量和麻烦,数值也不一定非得是-1或1。
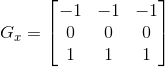
说明:这是一个典型的梯度算子(离散微分算子),通常情况下,用法是![]()
原理和其他边缘检测算子是一样的(参考sobel算子的说明)。 这个G 表征了梯度的幅度大小,借用Wiki上的两张图片可以看到效果
Sobel边缘检测
说明:这个算子怎么看都和Perwitt梯度差不多,原理也是一样的:当不处于边缘时,像素值比较平滑,卷积计算得到的各个计算结果相差不大,-1和1,-2和2,大家相互抵消,基本显现出来的,就是近似于黑色RGB =(0,0,0);当碰到边缘时,由于两侧的值各不相同(例如,Gx遇到的左侧像素值为10,右侧为20,那么计算结果就是40),所以Sobel算子给出的结果,就会使这个边缘剧烈锐化,从而显现出来向深色靠拢(例如白色RGB=(255,255,255))。
事实上,Sobel的表达式不是唯一的,上面这个式子是计算量最小的。不嫌麻烦和计算量的话,你可以随意构造类似的自己的Sobel矩阵,例如
Laplacian锐化
Laplacian锐化(n>0,n越大,锐化效果越明显),
这个算子一目了然,和前面的锐化算子稍有不同,这里不会把平滑区变成完全的RGB=(000)的黑色。该算子能起取锐化效果,就是使亮点更亮(比如说让白点更白),当然你如果想反着来,n取负值就可以了。同样取决于你想要的计算量和锐化程度,周围值不必是1,但一般情况下要求对称。
参考
【1】 http://songho.ca/dsp/
【2】https://en.wikipedia.org/wiki/Exponential_decay
【3】https://en.wikipedia.org/wiki/Sobel_operator

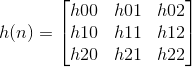
![input[3,3]=\begin{bmatrix} 10 &20 &30\\ 40 &50 &60\\ 70 &80 &90 \end{bmatrix}](http://img.e-com-net.com/image/info8/55debdc0a0514157a08b8e3e069039b0.gif)
![kernel[3,3]=\begin{bmatrix} 1&2&1\\ 2&4&2\\ 1&2&1 \end{bmatrix} =\begin{bmatrix} 1\\2\\1 \end{bmatrix} \begin{bmatrix} 1&2&1 \end{bmatrix}](http://img.e-com-net.com/image/info8/852c3f25274747fd8c105179168a758f.gif)