【matlab】遗传算法
本文源代码下载
解决最优化问题的方法
- 传统搜索方法
无约束优化、约束优化、线性规划、整数规划、二次规划……
能保证找到最优解
- 智能优化算法
现代启发式算法，是一种具有全局优化性能、通用性强且适合于并行处理的算法。
遗传算法、粒子群算法、鱼群算法、蚁群 算法……不能保证找到精确最优解
不能保证找到精确最优解
智能优化算法种类：
- 遗传算法(Genetic Algorithm，GA)
物竞天择，设计染色体编码，根据适应值函数进行染色体选择、交叉和变异操作，优化求解
- 人工神经网络算法(ANN)
模仿生物神经元，透过神经元的信息传递、训练学习联想，优化求解
- 模拟退火算法(Simulated Annealing，SA)
模仿金属物质退火过程
- 粒子群算法(Particle Swarm，PS)
……蚁群、蜂群、鱼群、布谷鸟、蝙蝠……
智能优化算法的特点
它们的共同特点都是从任一解出发，按照某种机制，以一定的概率在整个求解空间中探索最优解 。由于它们可以把搜索空间扩展到整个问题空间， 因而具有全局优化性能。
遗传算法
- 遗传算法作为一种有效的工具，已广泛地应用于最优化问题求解之中。
- 遗传算法是一种基于自然群体遗传进化机制的自适应全局优化概率搜索算法。
遗传算法的搜索机制
- 遗传算法模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象。
- 在每次迭代中都保留一组候选解，并按 某种指标从解群中选取较优的个体，利用遗传算子(选择、交叉和变异)对这些个体进行 组合，产生新一代的候选解群。
生物进化与遗传算法对应关系
由于遗传算法是由进化论和遗传学机理而产生的搜索算法，所以在这个算法中会用到很多生物遗传学知识，下面是我们将会用来的一些术语说明：
-
染色体
染色体又可以叫做基因型个体(individuals),一定数量的个体组成了群体(population),群体中个体的数量叫做群体大小。
-
基因
基因是串中的元素，基因用于表示个体的特征。例如有一个串S=1011，则其中的1，0，1，1这4个元素分别称为基因。它们的值称为等位基因(Alleles)。
-
基因位点
基因位点在算法中表示一个基因在串中的位置称为基因位置(Gene Position)，有时也简称基因位。基因位置由串的左向右计算，例如在串 S=1101 中，0的基因位置是3。
-
特征值
在用串表示整数时，基因的特征值与二进制数的权一致；例如在串 S=1011 中，基因位置3中的1，它的基因特征值为2；基因位置1中的1，它的基因特征值为8。
-
适应度
各个个体对环境的适应程度叫做适应度(fitness)。为了体现染色体的适应能力，引入了对问题中的每一个染色体都能进行度量的函数，叫适应度函数。 这个函数是计算个体在群体中被使用的概率。
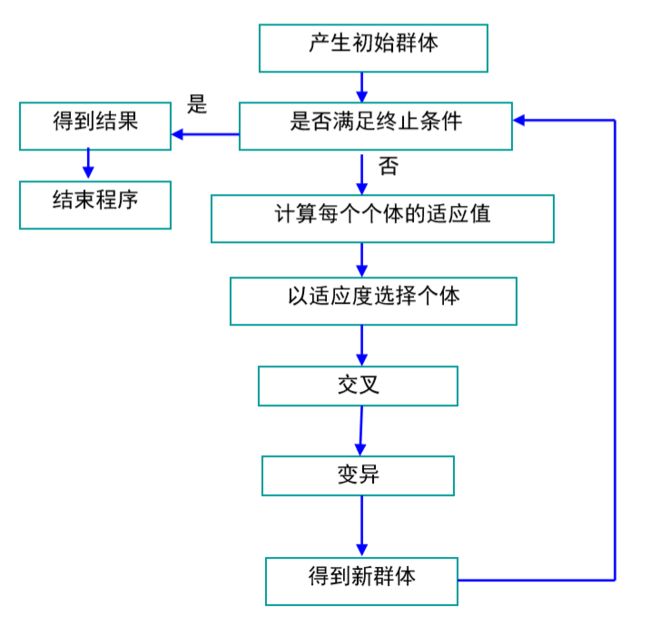
遗传算法具体步骤
- 选择编码策略，把参数集合（可行解集合）转换染色体结构空间；
- 定义适应函数，便于计算适应值
- 确定遗传策略，包括选择群体大小，选择、交叉、变异方法以及确 定交叉概率、变异概率等遗传参数
- 随机产生初始化群体
- 计算群体中的个体或染色体解码后的适应值
- 按照遗传策略，运用选择、交叉和变异算子作用于群体，形成下一 代群体
- 判断群体性能是否满足某一指标，或者已完成预定的迭代次数，不满足则返回第五步，或者修改遗传策略再返回第六步
遗传算法的基本操作
遗传算法计算优化的过程就如同生物学上生物遗传进化的过程，主要有三个基本操作（或算子）：
- 选择（Selection）
根据各个个体的适应值，按照一定的规则或方法，从第
代群体
中选择出一些优良的个体遗传到下一代群体
中。
- 交叉（Crossover）
将群体
内的各个个体随机搭配成对，对每一个个体，以某个概率
(称为交叉概率，crossvoer rate)交换它们之间的部分染色体。
- 变异（Mutation）
对群体
中的每一个个体，以某一概率
(称为变异概率，mutation rate)改变某一个或一些基因座上基因值为其它的等位基因。
如何设计遗传算法
采用二进制形式来解决编码问题，即将某个变量值代表的个体表示为一个{0, 1}二进制串。
- 1.串的长度取决于求解的精度
exm ：假设求解精度为保留六位小数，由于区间 [-1, 2] 的长度为 3，则必须将该区间分为
等分。因为 
，所以编码所用的二进制串至少需要22位。
- 2.二进制串
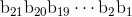与 [a, b] 内实数的一一映射
可以现转换成十进制数，再转换成[a,b]内的实数，即：
exm：二进制串 a=<1000101110110101000111> 其对应的十进制数为：
x'=(1000101110110101000111) =2288967
转化到 [-1, 2] 内的实数为：
- 如何产生初始种群
1.初始种群的生成是随机的
2.规模太小会出现近亲繁殖，产生病态基因，造成有效等位基因先天缺乏
3.规模太大，结果难以收敛且浪费资源，稳健性下降
4.规模的建议值为10~100
- 如何定义适应函数
1.GA在搜索中不依靠外部信息，仅以适应函数为依据，利用群体中每个染色体(个体)的适应值来进行搜索。以染色体适应值的大小来确定该染色体被遗传到下一代群体中的概率
2.群体中的每个染色体都需要计算适应值
3.适应函数一般由目标函数变换而成
适应函数常见形式：
对直接将目标函数转化为适应函数
(1)若目标函数为最大化问题：
(2)若目标函数为最小化问题：
界限构造法:
- 目标函数为最大化问题
其中
为
的最小估计值
- 目标函数为最小化问题
其中
为的最大估计值
tips缺点：
可能不满足轮盘赌选择中概率非负的要求； 某些代求解的函数值分布上相差很大，由此得到的评价适应值可能不利于体现群体的评价性能，影响算法的性能。
- 如何进行遗传操作(复制、交叉、变异)
选择
选择(复制)操作把当前种群的染色体按与适应值成正比例的概率复制到新的种群中
主要思想: 适应值较高的染色体体有较大的选择(复制)机会
（1）轮盘赌选择
√ 将种群中所有染色体的适应值相加求总和，染色体适应值按其比例转化为选择概率
√ 产生一个在0与总和之间的的随机数m
√ 从种群中编号为1的染色体开始，将其适应值与后续染色体的适应值相加，直到累加和等于或大于m
(2)其他选择法
√ 随机遍历抽样(Stochastic universal sampling)
√ 局部选择(Local selection)
√ 截断选择(Truncation selection)
√ 竞标赛选择(Tournament selection)
tips: 选择操作的作用效果是提高了群体的平均适应值(低适应值个体趋于淘汰，高适应值个体趋于选择 )，但这也损失了群体的多样性。
交叉
√ 遗传交叉(杂交、交配、有性重组)操作发生在两个染色体之间，由两个被称之为双亲的父代染色体，经杂交以后，产生两个具有双亲的部分基因的新染 色体，从而检测搜索空间中新的点。
√ 选择(复制)操作每次作用在一个染色体上，而交叉操作每次作用在从交配池中随机选取的两个个体上(交叉概率Pc)。
√ 交叉产生两个子染色体，它们与其父代不同，且彼此也不同，每个子染色体都带有双亲染色体的遗传基因。
（1）单点交叉
- 在双亲的父代染色体中随机产生一个交叉点位置
- 在交叉点位置分离双亲染色体
- 相互交叉点位置右边的基因码产生两个子代染色体
- 交叉概率
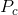一般范围为(60%,90%)，平均约80%
以|代表交叉点位置
父代:1111|11111111
0000|00000000
子代:111100000000
000011111111
单点交叉操作可以产生与父代染色体完全不同的子代染色体；它不会改变父代染色体中相同的基因。
但当双亲染色体相同时，交叉操作是不起作用的。
假如交叉概率＝50%,则交配池中50%的染色体(一半染色体)将进行交叉操作，余下的50%的染色体进行选择( 复制)操作。
GA利用选择和交叉操作可以产生具有更高平均适应值和更好染色体的群体。
变异
√ 比起选择和交叉操作，变异操作是GA中的次要操作，但它在恢复群体中失去的多样性方面具有潜在的作用
√ 以变异概率Pm改变染色体的某一个基因，当以二进制编码时，变异的基因由0变成1，或者由1变成0
√ 变异概率Pm一般介于1/种群规模与1/染色体长度之间，平均约1-2%
- 如何产生下一代种群
- 如何定义停止准则
1.进化代数太小，种群还没有成熟，算法不容易收敛
2.进化代数太大，种群早熟不可能再收敛，继续进化没有意义
3.进化代数的建议值为100~500
停止准则
种群中个体的最大适应值超过预设定值
种群中个体的平均适应值超过预设定值
种群中个体的进化代数超过预设定值
伪代码描述
Procedure Genetic Algorithm
begin t = 0 ;% 遗传代数
初始化 P(t) ; % 初始化
计算 P(t) 的适应值 ;
while (不满足停止准则) do
begin
t = t+1 ;
从P(t-1)中选择 P(t) ; % 选择
重组 P(t) ; % 交叉和变异
计算 P(t) 的适应值;
end
end
遗传算法的应用
- 函数优化
- 组合优化
- 生产调度问题
- 自动控制
- 机器人智能控制
- 图象处理和模式识别
- 机器学习
- 图象处理和模式识别
- 机器学习
matlab工具箱函数
GA函数语法格式[x,fval,reason]=ga(@fitnessfun,nvars,options)
√ x为经过遗传进化以后自变量最佳染色体返回值
√ fval为最佳染色体的适应度
√ reason为算法停止的原因
√ @fitnessfun为适应度句柄函数
√ nvars为目标函数自变量的个数
√ options为算法的属性设置，通过函数gaoptimset赋予
工具箱核心函数的用法
- 函数gaoptimset实现的功能为,设置遗传算法的参数和 句柄，语法格式:
options=gaoptimset(‘PropertyName1’,‘PropertyValue1’ , PropertyName2’,‘PropertyValue2’,……)
- 可以将前一次运行得到的最后种群作为下一次运行的初始种 群，可以得到更好的结果
[x,fval,reason,output,final_pop]=ga(@fitnessfun,nvars)
- final_pop为本次运行得到的最后种群，可以作为下次的初始种群。
options=gaoptimset(‘InitialPopulation’,‘final_pop’); [x,fval,reason,output,final_pop2]=ga(@fitnessfun,nvar s,options);
gaoptimset的参数：
| 函数gaoptimset属性 | ||
| 属性名 | 默认值 | 实现功能 |
| PopInitRange | [0,1] | 初始种群生成区间 |
| PopulationSize | 20 | 种群规模 |
| CrossoverFraction | 0.8 | 交叉概率 |
| MigrationFracition | 0.2 | 变异概率 |
| Generations | 100 | 超过进化代数时算法停止 |
| TimeLimit | Inf | 超过运算时间限制时算法停止 |
| FitnessLimit | -Inf | 最佳个体等于或小于适应度阈值时算法停止 |
| StallGenLimit | 50 | 超过连续代数不进化则算法停止 |
| StallTimeLimit | 20 | 超过连续时间不进化则算法停止 |
| InitialPopulation | [] | 初始化种群 |
| PlotFcns | [] | 绘图函数，可供选择的有@gaplotbestf,@gaplotbestindiv等 |