余辉亮的学习笔记

dso详解--dso原理的"大卸八块"

本篇文章摘自:高翔的最新的知乎文章,转载请注明原文链接,同时感谢翔哥(半闲居士)一直以来对国内vslam做出的贡献.

原文地址: https://zhuanlan.zhihu.com/p/29177540 本人对原文稍微做了细小的改动,如有不明,请查看原文链接.

DSO（Direct Sparse Odometry），是慕尼黑工业大学（Technical University of Munich, TUM）计算机视觉实验室的雅各布.恩格尔（Jakob Engel）博士，于2016年发布的一个视觉里程计方法（期刊论文见[1]，实验室主页见 Computer Vision Group ）。在SLAM领域，DSO属于稀疏直接法，据论文称能达到传统特征点法的五倍速度（需要降低图像分辨率），并保持同等或更高精度，代码见： JakobEngel/dso 。然而，由于某些历史和个人的原因，DSO的代码清晰度和可读性，明显弱于其他SLAM方案如ORB、SVO、okvis等，使得研究人员很难以它为基础，展开后续的研究工作。因此，本文希望从理论和实现层面解读DSO，尝试为其他对DSO感兴趣的研究人员提供一些有益的思路和观点。

注：

为了读懂本文，我们假定读者已具有视觉SLAM的基本知识，否则，请先阅读相关材料。另外，如果读过DSO论文或代码，可能对本文有更好的理解。
由于知乎平台分辨率限制，插图可能不够清晰。如果能图像质量有更高要求，请联系作者：gao.xiang.thu at gmail dot com.
由于本文较长，我会花几次时间进行更新，应读者要求先发布草稿版。

以下是本文的提纲：

提纲

概述
流程框架
滑动窗口
光度标定
评述
资料与参考文献

概述

DSO属于稀疏直接法的视觉里程计。它不是完整的SLAM，因为它不包含回环检测、地图复用的功能。因此，它不可避免地会出现累计误差，尽管很小，但不能消除。DSO目前开源了单目实现，双目DSO的论文已被ICCV接收，但目前未知是否开源。

DSO是少数使用纯直接法（Fully direct）计算视觉里程计的系统之一。相比之下，SVO[2]属于半直接法，仅在前端的Sparse model-based Image Alignment部分使用了直接法，之后的位姿估计、bundle adjustment，则仍旧使用传统的最小化重投影误差的方式。而ORB-SLAM2[3]，则属于纯特征法，计算结果完全依赖特征匹配。从方法上来说，DSO是新颖、独树一帜的。

直接法相比于特征点法，有两个非常不同的地方：

特征点法通过最小化重投影误差来计算相机位姿与地图点的位置，而直接法则最小化光度误差（photometric error）。所谓光度误差是说，最小化的目标函数，通常由图像之间的误差来决定，而非重投影之后的几何误差。
直接法将数据关联（data association）与位姿估计（pose estimation）放在了一个统一的非线性优化问题中，而特征点法则分步求解，即，先通过匹配特征点求出数据之间关联，再根据关联来估计位姿。这两步通常是独立的，在第二步中，可以通过重投影误差来判断数据关联中的外点，也可以用于修正匹配结果（例如[4]中提到的类EM的方法）。

由于这个原因，DSO会一直求解一个比较复杂的优化问题，我们很难将它划分为像特征点法那样一步一步的过程。DSO甚至没有“匹配点”这个概念。每一个三维点，从某个主导帧（host frame）出发，乘上深度值之后投影至另一个目标帧（target frame），从而建立一个投影残差（residual）。只要残差在合理范围内，就可以认为这些点是由同一个点投影的。从数据关联角度看，在这个过程中并没有a1-b1, a2-b2这样的关系，也可能存在a1-b1, a2-b1, a3-b1这样的情况。但是DSO并不在意这些，只要残差不大，我们就看成是同一个点。这是很重要的一点。在特征点法中，我们可以找到一个地图点分别在哪些帧中被看到，乃至找到各帧中的图像描述子是什么；但在DSO中，我们会尝试把每个点投影到所有帧中，计算它在各帧中的残差，而并不在意点和点之间的一一对应关系。

从后端来看，DSO使用一个由若干个关键帧组成的滑动窗口作为它的后端。这个窗口在整个VO过程中一直存在，并有一套方法来管理新数据的加入以及老数据的去除。具体来说，这个窗口通常保持5到7个关键帧。前端追踪部分，会通过一定的条件，来判断新来的帧是否可作为新的关键帧插入后端。同时，如果后端发现关键帧数已经大于窗口大小，也会通过特定的方法，选择其中一个帧进行去除。请注意被去除的帧并不一定是时间线上最旧的那个帧，而是会有一些复杂条件的。

后端除了维护这个窗口中的关键帧与地图点外，还会维护与优化相关的结构。特别地，这里指Gauss-Newton或Levenburg-Marquardt方法中的Hessian矩阵和b向量（仅先验部分）。当我们增加新的关键帧时，就必须扩展H和b的维度；反之，如果需要去掉某个关键帧（以及它携带的地图点）时，也需要降低H和b的维度。这个过程还需要将被删掉帧和点的信息，转移到窗口内剩余帧当中，这一步被称为边缘化（Marginalization）。

由于直接法需要比较图像信息，其结果容易受光照干扰。于是，DSO提出了光度标定，认为对相机的曝光时间、暗角、伽马响应等参数进行标定后，能够让直接法更加鲁棒。对于未进行光度标定的相机，DSO也会在优化中动态估计光度参数（具体来说，是一个仿射变化的参数，记作a和b）。这个过程建模了相机的成像过程，因此对于由相机曝光不同引起的图像明暗变化，会有更好的表现。但是，如果由于环境光源发生变化，光度标定也是无能为力的。

本文第2节介绍DSO基本框架和流程。第3节介绍滑动窗口内的最小二乘问题、雅可比、边缘化。第4节介绍光度标定。第5节会给出我个人对DSO的一些评述。最后列出参考文献。DSO相关的实验、比较结果，请参见作者原始论文，在此不作叙述。

2. 框架流程

2.1 代码框架与数据表示

现在我们来看DSO的大体框架。我去除了一些不重要的类和结构，方便读者阅读。

DSO整体代码由四个部分组成：系统与各算法集成于src/FullSystem，后端优化位于src/OptimizationBackend，这二者组成了DSO大部分核心内容。src/utils和src/IOWrapper为一些去畸变、数据集读写和可视化UI代码。先来看核心部分的FullSystem和OptimizationBackend。

如上图上半部分所示，在FullSystem里，DSO致力于维护一个滑动窗口内部的关键帧序列。每个帧的数据存储于FrameHessian结构体中，FrameHessian即是一个带着状态变量与Hessian信息的帧。然后，每个帧亦携带一些地图点的信息，包括：

pointHessians是所有活跃点的信息。所谓活跃点，是指它们在相机的视野中，其残差项仍在参与优化部分的计算；
pointHessiansMarginalized是已经边缘化的地图点。
pointHessiansOut是被判为外点（outlier）的地图点。
以及immaturePoints为未成熟地图点的信息。

在单目SLAM中，所有地图点在一开始被观测到时，都只有一个2D的像素坐标，其深度是未知的。这种点在DSO中称为未成熟的地图点：Immature Points。随着相机的运动，DSO会在每张图像上追踪这些未成熟的地图点，这个过程称为trace——实际上是一个沿着极线搜索的过程，十分类似于svo的depth filter。Trace的过程会确定每个Immature Point的逆深度和它的变化范围。如果Immature Point的深度（实际中为深度的倒数，即逆深度）在这个过程中收敛，那么我们就可以确定这个未成熟地图点的三维坐标，形成了一个正常的地图点。具有三维坐标的地图点，在DSO中称为PointHessian。与FrameHessian相对，PointHessian亦记录了这个点的三维坐标，以及Hessian信息。

与很多其他SLAM方案不同，DSO使用单个参数描述一个地图点，即它的逆深度。而ORB-SLAM等多数方案，则会记录地图点的x,y,z三个坐标。逆深度参数化形式具有形式简单、类似高斯分布、对远处场景更为鲁棒等优点[5]，但基于逆深度参数化的Bundle adjustment，每个残差项需要比通常的BA多计算一个雅可比矩阵。为了使用逆深度，每个PointHessian必须拥有一个主导帧（host frame），说明这个点是由该帧反投影得到的。

于是，滑动窗口的所有信息，可以由若干个FrameHessian，加上每个帧带有的PointHessian来描述。所有的PointHessian又可以在除主导帧外的任意一帧中进行投影，形成一个残差项，记录于PointHessian::residuals中。所有的残差加起来，就构成了DSO需要求解的优化问题。当然，由于运动、遮挡的原因，并非每个点都可以成功地投影到其余任意一帧中去，于是我们还需要设置每个点的状态：有效的/被边缘化的/无效的。不同状态的点，被存储于它主导帧的pointHessians/pointHessianMarginalized/PointHessiansOut三个容器内。

除此之外，DSO将相机的内参、曝光参数等信息，亦作为优化变量考虑在内。相机内参由针孔相机参数fx, fy, cx, cy表达，曝光参数则由两个参数a,b描述。这部分内容在光度标定一节内。

后端优化部分单独具有独立的Frame, Point, Residual结构。由于DSO的优化目标是最小化能量（energy，和误差类似），所以有关后端的类均以EF开头，且与FullSystem中存储的实例一一对应，互相持有对方的指针。优化部分由EnergyFunctional类统一管理。它从FullSystem中获取所有帧和点的数据，进行优化后，再将优化结果返回。它也包含整个滑动窗口内的所有帧和点信息，负责处理实际的非线性优化矩阵运算。

2.2 VO流程

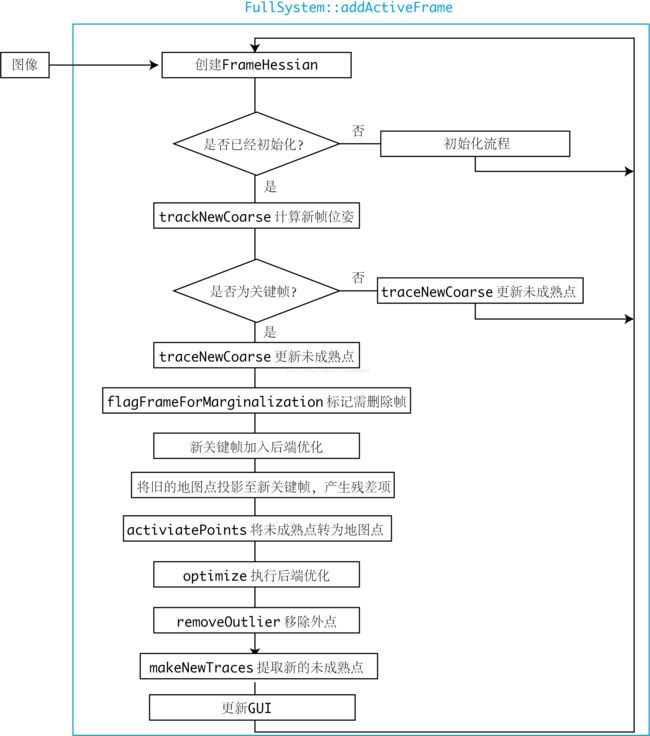
每当新的图像到来时，DSO将处理此图像的信息，流程如下：

尽管没有解释每一步的具体用意，但可以看出DSO的大致流程。从上图可以简单总结出DSO的行为：

对于非关键帧，DSO仅计算它的位姿，并用该帧图像更新每个未成熟点的深度估计；
后端仅处理关键帧部分的优化。除去一些内存维护操作，对每个关键帧主要做的处理有：增加新的残差项、去除错误的残差项、提取新未成熟点。
整个流程在一个线程内，但内部可能有多线程的操作。

3. DSO详细介绍

3.1 残差的构成与雅可比

在VO过程中，DSO会维护一个滑动窗口，通常由5-7个关键帧组成，流程如前所述。DSO试图将每个先前关键帧中的地图点投影到新关键帧中，形成残差项。同时，会在新关键帧中提取未成熟点，并希望它们演变成正常地图点。在实际当中，由于运动、遮挡的原因，部分残差项会被当作outlier，最终剔除；也有部分未成熟地图点无法演化成正常地图点，最终被剔除。

滑动窗口内部构成了一个非线性最小二乘问题。表示成因子图（或图优化）的形式，如下所示：

每一个关键帧的状态为八维：六自由度的运动位姿加上两个描述光度的参数；每个地图点的状态变量为一维，即该点在主导帧（Host）里的逆深度。于是，每个残差项（或能量项E），将关联两个关键帧与一个逆深度。事实上，还有一个全局的相机内参数亦参与了优化，但未在此图中表示。

现在我们来考虑如何计算残差。这部分推导和LSD-SLAM的会议论文[6]，以及我的书[7]是类似的。如果读者觉得有困难，可以参照它们。

设相机模型由针孔模型描述，那么内参矩阵为：

$K = \left[ {\begin{array}{*{20}{c}} {{f_x}}&{}&{{c_x}}\\ {}&{{f_y}}&{{c_y}}\\ 0&0&1 \end{array}} \right],\qquad {K^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {f_x^{ - 1}}&{}&{ - f_x^{ - 1}{c_x}}\\ {}&{f_y^{ - 1}}&{ - f_y^{ - 1}{c_y}}\\ {}&{}&1 \end{array}} \right]$

设有两个帧，一个称为Host，一个称Target，它们各自到世界坐标的变换矩阵记为，这二者又可以拆开为旋转和平移。考虑Host帧中一个像素点：

其中为该点的像素坐标，这里使用了齐次坐标以方便矩阵运算。同时，该点的逆深度为：

其中为该点的深度值。那么，这个点在Target帧中的投影为：

$\begin{array}{ll} {\rho _T^{-1}}{x_T} &= K\underbrace {{T_{TW}}T_{HW}^{ - 1}}_{{T_{TH}}}\underbrace {{K^{ - 1}}\frac{1}{{{\rho _H}}}{x_H}}_{{p_W}}\\ &= K\left( {{R_{TH}}{p_W} + {t_{TH}}} \right) \\ \end{array}$

注：(i). 为方便起见，我们略去了此公式中的齐次坐标至非齐次的转换，默认它们是自动转换的；(ii). 我们定义了中间变量，即点的世界坐标，以及Host至Target的相对变换。

由此可以定义该点的残差。设Host和Target的图像分别是，那么残差为：

但是在实现中，DSO会同时估计图像的光度参数a,b，所以在计算误差时，会用到去掉光度参数之后的那个值。但是这里我们先不谈光度标定部分，所以暂时把看成原始图像。

接下来我们要谈论雅可比。在完整DSO中，雅可比由三部分组成：

图像雅可比，即图像梯度；
几何雅可比，描述各量相对几何量，例如旋转和平移的变化率；
光度雅可比，描述各个量相对光度参数的雅可比；

作者认为，几何和光度的雅可比，相对自变量来说通常是光滑函数；而图像雅可比则依赖图像数据，不够光滑；所以，在优化过程中，几何和光度的雅可比仅在迭代开始时计算一次，此后固定不变[1]。而图像雅可比则随着迭代更新。这种做法称为First-Estimate-Jacobian（FEJ），在VIO中也会经常用到[8]。它可以减小计算量、防止优化往错误的地方走太多，也可以在边缘化过程中保证零空间的维度不会降低，后者我们还要在后文继续谈。

下面来看几何雅可比的具体计算。记为李代数表示的，并定义：

根据[7]的推导加一些变化，可知：

$\frac{{\partial {x_T}}}{{\partial {\xi _T}}} = \left[ {\begin{array}{*{20}{c}} {{\rho _T}{f_x}}&0&{ - {\rho _T}{u}{f_x}}&{ - {u}{v}{f_x}}&{\left( {1 + u^2} \right){f_x}}&{ - v{f_x}}\\ 0&{{\rho _T}{f_y}}&{ - {f_y}{\rho _T}{v}}&{ - \left( {1 + {v^2}} \right){f_y}}&{{f_y}uv}&{{f_y}u} \end{array}} \right]$

再考虑对于Host帧中的逆深度之雅可比：

$\frac{{\partial {x_T}}}{{\partial {\rho _H}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {x_T}}}{{\partial u}}}&{\frac{{\partial {x_T}}}{{\partial v}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial {\rho _H}}}}\\ {\frac{{\partial v}}{{\partial {\rho _H}}}} \end{array}} \right]$

显然：

$\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {x_T}}}{{\partial u}}}&{\frac{{\partial {x_T}}}{{\partial v}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_x}}&{{f_y}} \end{array}} \right]$

对于后者，首先记：

那么：

$u = {\rho _T}\left( {\rho _H^{ - 1}{a_1} + {t_1}} \right) = \frac{{\rho _H^{ - 1}{a_1} + {t_1}}}{{\rho _H^{ - 1}{a_3} + {t_3}}} = \left( {{a_1} + {\rho _H}{t_1}} \right)\left( {{a_3} + {\rho _H}{t_3}} \right)^{-1}$

其中下标1表示取第一行，3表示第三行。于是

$\begin{array}{ll} \frac{{\partial u}}{{\partial {\rho _H}}} &= {t_1}{\left( {{a_3} + {\rho _H}{t_3}} \right)^{ - 1}} + \left( {{a_1} + {\rho _H}{t_1}} \right)\frac{{ - {t_3}}}{{{{\left( {{a_3} + {\rho _H}{t_3}} \right)}^2}}}\\ & = {t_1}{\left( {{a_3} + {\rho _H}{t_3}} \right)^{ - 1}} - u{t_3}{\left( {{a_3} + {\rho _H}{t_3}} \right)^{ - 1}} \\&= \left( {{t_1} - u{t_3}} \right)\frac{{{\rho _T}}}{{{\rho _H}}} \end{array}$

最后的式子中我们重新把代回去，使得式子更加简洁。同理有：

于是得：

$\frac{{\partial {x_T}}}{{\partial {\rho _H}}} = \left[ {\begin{array}{*{20}{c}} {{f_x}\left( {{t_1} - u{t_3}} \right){\rho _T}/{\rho _H}}\\ {{f_y}\left( {{t_2} - v{t_3}} \right){\rho _T}/{\rho _H}} \end{array}} \right]$

接下来考虑残差相对于相机内参的雅可比，这部分相对于其余部分稍为复杂，我们仅展示残差对之导数，其余部分类似可得，因此留给读者。由于：

${x_T} = K\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right],\quad \left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = {\rho _T}\left( {\frac{1}{{{\rho _H}}}R\underbrace {{K^{ - 1}}{x_H}}_P + t} \right)$

该式略去了的下标，以保持行文简洁。展开后式，有：

$\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rho _T}\left( {\rho _H^{ - 1}r_1^TP + {t_1}} \right)}\\ {{\rho _T}\left( {\rho _H^{ - 1}r_2^TP + {t_2}} \right)}\\ {{\rho _T}\left( {\rho _H^{ - 1}r_3^TP + {t_3}} \right)} \end{array}} \right]$

于是：

${x_T} = \left[ {\begin{array}{*{20}{c}} {{f_x}\underbrace {{\rho _T}\left( {\rho _H^{ - 1}r_1^TP + {t_1}} \right)}_u + {c_x}}\\ {{f_y}\underbrace {{\rho _T}\left( {\rho _H^{ - 1}r_2^TP + {t_2}} \right)}_v + {c_y}}\\ {\underbrace {{\rho _T}\left( {\rho _H^{ - 1}r_3^TP + {t_3}} \right)}_1} \end{array}} \right]$

现在想要求第一行关于之导数，由链式法则：

而

第一项中，由前述，有：

于是

$\begin{array}{l} \frac{{\partial u}}{{\partial P}} = \left( {\rho _H^{ - 1}{r_1}} \right){\left( {\rho _H^{ - 1}r_3^TP + {t_3}} \right)^{ - 1}} - \left( {\rho _H^{ - 1}r_1^TP + {t_1}} \right)\frac{{\rho _H^{ - 1}{r_3}}}{{{{\left( {\rho _H^{ - 1}r_3^TP + {t_3}} \right)}^2}}}\\ = {\rho _T}/{\rho _H}\left( {{r_1} - {r_3}u} \right) \end{array}$

第二项：

因此：

$\begin{array}{ll} \frac{{\partial {x_{T,1}}}}{{\partial {f_x}}} &= u + {f_x}\frac{{\partial u}}{{\partial {f_x}}} = u + {f_x}{\rho _T}/{\rho _H}{\left( {{r_1} - {r_3}u} \right)^T}\left( {\begin{array}{*{20}{c}} { - f_x^{ - 1}{P_1}}\\ 0\\ 0 \end{array}} \right)\\ & = u + {\left( {r_{31}}u- {{r_{11}} } \right)^T}{P_1}\rho_T/\rho_H \end{array}$

于是，得到了投影点关于的导数。关于的结论可类似推出，不再赘述。以上计算均实现于PointFrameResidual::linearize函数。

值得一提的是，在DSO中，每个投影点，除了自身的位置之外，一共提供八维残差，这是为了更好利用该点的信息。这八维残差由这个点与周围几个点组成的Pattern定义，如下图所示：

选八个点是为了方便SSE（Super Strong Erection）（雾），其实在settings.cpp中还有许多别的Pattern。所以，在DSO的直接法中，我们实际上假设了这八个点在不同图像中保持灰度不变。并且，它们在优化中共享中间点的深度，所以也不能简单地看成八个独立的点。

3.2 滑动窗口的维护与边缘化

若干和关键帧，与它们关联的地图点组成的残差项，构成了整个滑动窗口中的内容。为了优化这些帧和点，我们会利用Gauss-Newton或Levernberg-Marquardt方法进行迭代。在迭代中，所有的残差项可以拼成一个大型的线性方程：

其中分别为拼接后的雅可比、权重和残差，为整体的优化更新量。左侧可以记成：，即Hessian矩阵。这个矩阵在整个优化过程中都会一直维护于内存中。注意这种做法和ORB-SLAM2是不同的。在ORB-SLAM2的后端中，我们会不停地重构整个优化问题，求解，然后存储优化后的结果，但这个H矩阵是不会一直存在的。而在DSO中，由于H是一直维护的，所以之后的优化可以利用先前的结果，或者说，先前的优化为下一步提供了先验（Prior）。但是，为了维护这个H信息，DSO必须手动地增加/删除每一个帧和点，而不像ORB-SLAM2那样，可以无视帧和点的变化。

我们知道，H实际上有一个特殊的形状（箭头形矩阵，Arrow-like Matrix）[1,7,9]，如下图所示：

众所周知，这个形状是由BA本身的结构导致的。把它的分块记为：

那么右下角的是一个对角块矩阵（因为没有结构的先验，即点——点的残差）。块的大小取决于地图点的参数化维度，在DSO中是一维，在ORB-SLAM2中是三维。接下来，在传统BA中（类似于ORB-SLAM2）的做法是这样的：

通过图优化构建这个H；
用高斯消元法（即舒尔补）将右下角部分消元：

$\left[ \begin{matrix} \bm{I} & -\bm{EC^{-1}} \\ \bm{0} & \bm{I} \end{matrix}\right] \left[ \begin{matrix} \bm{B} & \bm{E} \\ \bm{E^T} & \bm{C} \end{matrix}\right] \left[ \begin{array}{l} \Delta \bm{x}_c \\ \Delta \bm{x}_p \end{array} \right] = \left[ \begin{matrix} \bm{I} & -\bm{EC^{-1}} \\ \bm{0} & \bm{I} \end{matrix} \right] \left[ \begin{array}{l} \bm{v} \\ \bm{w} \end{array} \right] .$

即：

$\left[ \begin{matrix} \bm{B} - \bm{E}\bm{C}^{-1}\bm{E}^T & \bm{0} \\ \bm{E}^T & \bm{C} \end{matrix} \right] \left[ \begin{array}{l} \Delta \bm{x}_c \\ \Delta \bm{x}_p \end{array} \right] = \left[\begin{array}{l} \bm{v} - \bm{E}\bm{C}^{-1}\bm{w} \\ \bm{w} \end{array}\right].$

此时方程解耦，于是先解左上部分（维度很小）；再用左上部分的结果解右下部分。

这个过程也称为边缘化（Marginalization），此时我们边缘化掉了所有的点，将他们的信息归到了位姿部分中，形成了相机位姿部分的先验。这部分知识，对于每位SLAM研究者来说应当是熟知的。

那么在DSO中，有哪些地方用了边缘化？

首先，DSO的BA，也和传统BA一样，有上述步骤。因此DSO在解BA时，边缘化了所有点的信息，计算优化的更新量。然而，与传统BA不同的是，DSO的左上角部分，即公式中的，并非为对角块，而是有先验的。传统BA中，这部分为对角块，主要原因是不知道相机运动的先验，而DSO的滑动窗口，则通过一定手段计算了这个先验。这里的先验主要来自两个部分：

边缘化某个点时，这个点的共视帧之间产生先验；
边缘化某个帧时，在窗口内其他帧之间产生先验；

这里的“边缘化”，具体的操作和上面讲的边缘化，是一样的。也就是说，通过舒尔补，用矩阵的一部分去消元另一部分。然而实际操作的含义却有所不同。在BA的边缘化中，我们希望用边缘化加速整个问题的求解，但是解完问题后，这些帧和点仍旧是存在于窗口中的！而滑动窗口中的边缘化，是指我们不再需要这个点/这个帧。当它被边缘化时，我们将它的信息传递到了之后的先验中，而不会再利用这个点/这个帧了！请读者务必理清这层区别，否则在理解过程中会遇到问题。我们不妨将后者称为“永久边缘化”，以示区分。

那么DSO如何永久边缘化某个帧或点？它遵循以下几个准则：

如果一个点已经不在相机视野内，就边缘化这个点；
如果滑动窗口内的帧数量已经超过设定阈值，那么选择其中一个帧进行边缘化；
当某个帧被边缘化时，以它为主导的地图点将被移除，不再参与以后的计算。否则这个点将与其他点形成结构先验，破坏BA中的稀疏结构[10]。

在边缘化的过程，DSO维护了帧与帧间的先验信息（见EnergyFunctional::HM和bM），并将这些信息利用到BA的求解中去。

3.3 零空间，FEJ

在SLAM中，GN或LM优化过程中，状态变量事实上是存在零空间（nullspace）的。所谓零空间，就是说，如果在这个子空间内改变状态变量的值，不会影响到优化的目标函数取值。在纯视觉SLAM中，典型的零空间就是场景的绝对尺度，以及相机的绝对位姿。可以想象，如果将相机和地图同时扩大一个尺度，或者同时作一次旋转和平移，整个目标函数应该不发生改变。零空间的存在也会导致在优化过程中，线性方程的解不唯一。尽管每次迭代的步长都很小，但是时间长了，也容易让整个系统在这个零空间中游荡，令尺度发生漂移。

另一方面，由于边缘化的存在，如果一个点被边缘化，那它的雅可比等矩阵就要被固定于被边缘化之时刻，而其他点的雅可比还会随着时间更新，就使得整个系统中不同变量被线性化的时刻是不同的。这会导致零空间的降维——本应存在的零空间，由于线性化时刻的不同，反而消失了！而我们的估计也会变得过于乐观。

DSO作者提出了一个很好的例子以展现这件事情。见下图。

在这个例子中，我们最小化，那么显然这条曲线就是优化问题的最优解，正好是一维的零空间。但是，如果和在不同点上线性化，那么求得的可能会让这一维的零空间消失（如图例），这时最优解变成了一个点。

因此，在DSO实际使用时，仅在优化的初始时刻计算几何和光度的雅可比，并让它们在随后的迭代过程中保持不变，即First-Estimate-Jacobian。FEJ强制让每个点在同一个时刻线性化，从而回避了零空间降维的问题，同时可以降低很多计算量。DSO中的每个地图点，由前面定义的pattern产生8个残差项，这些残差项也会共享FEJ。由于几何和光度函数都比较光滑，实践当中FEJ近似是十分好用的。

3.4 其他零散的模块和算法

除去上述主干以外，DSO还有一些枝节上的算法，例如：

DSO是怎么初始化的？
DSO的CoarseTracker如何估计新帧的位姿？
未成熟点是如何转换到正常地图点的？

(TODO：待更新）

4. 光度标定

我发现已经有一些文章介绍DSO的光度标定了[11]，所以我考虑不再重复介绍一遍了。如果需要的话我会补上。

5. 评述

DSO的出现将直接法推进到一个相当成熟可用的地位，许多实验已表明它的精度与鲁棒性均优于现在的ORB-SLAM2，而相比之下LSD-SLAM则显然没有那么成熟。在我自己的实物相机实验中，我发现LSD-SLAM很难一次上手即通，而DSO则鲁棒的多。

在大部分数据集上，DSO均有较好的表现。虽然DSO要求全局曝光相机，但即使是卷帘快门的相机，只要运动不快，模糊不明显，DSO也能顺利工作。但是，如果出现明显的模糊、失真，DSO也会丢失。

我认为，直接法相比传统特征点法，最大的贡献在于，直接法以更整体、更优雅的方式处理了数据关联问题。特征点法需要依赖重复性较强的特征提取器，以及正确的特征匹配，才能得正确地计算相机运动。在环境纹理较好，角点较多时，这当然是可行的——不过直接法在这种环境下也能正常工作。然而，如果环境中出现了下列情况，对特征点法就不那么友善：

环境中存在许多重复纹理；
环境中缺乏角点，出现许多边缘或光线变量不明显区域；

这在实际图像中很常见，我们以道路环境为例（取自kitti）：

显然，路面上角点甚少，仅有车道线的起始/终止处存在角点，其他地方纹理不足；天空通常也没有纹理；路旁栏杆和障碍物重复纹理非常明显。这些都是特征点法必须面对的问题，所以特征点法通常只能依赖一些车辆、行人、交通告示板来确定明显的特征匹配，这会影响整个SLAM系统的稳定性。其根本原因在于：无法找到有用的匹配点、或者容易找到错误的匹配点。例如，车道线边缘上的点外观都非常相似，栏杆附近的点则由于栏杆本身纹理重复，容易出现错配。

而直接法，如前所示，则并不要求一一对应的匹配。只要先前的点在当前图像当中具有合理的投影残差，我们就认为这次投影是成功的。而成功与否，主要取决于我们对地图点深度以及相机位姿的判断，并不在于图像局部看起来是什么样子。举个例子，如果用特征法或光流法追踪某个位于边缘的像素，由于沿着边缘方向图像局部很相似，所以这个匹配或追踪的结果，可能被计算成此边缘方向的另一个点——这主要是因为图像局部的相似性；而直接法的约束则来自更为整体的相机位姿，所以即使单个点无法给出足够的信息，还可以靠其他点来修正它的投影关系，从而找到正确的投影点。

这是一把双刃剑。直接法给予我们追踪边缘、平滑区块的能力，但同时也要付出代价——正确的直接法追踪需要有一个相当不错的初始估计，还需要一个质量较好的图像。由于DSO严重依赖于使用梯度下降的优化问题求解，而它成功的前提，是目标函数从初始值到最优值之间一直是下降的。在图像质量不佳或者相机初始位姿给的不对的情况下，这件事情往往无法得到保证，所以DSO也会丢失。

这种做法一个显而易见的后果是，除非存储所有的关键帧图像，否则很难利用先前建好的地图。退一步说，即使有办法存储所有关键帧的图像，那么在重用地图时，我们还需要对位姿有一个比较准确的初始估计——这通常是困难的，因为你不知道误差已经累计到了多大的程度。而在特征点法中，地图重用则相对简单。我们只需存储空间中所有的特征点和它们的特征描述，然后匹配当前图像中看到的特征，计算位姿即可。

我们看到，数据关联和位姿估计，在直接法中是耦合的，而在特征点法中则是解耦的。耦合的好处，在于能够更整体性地处理数据关联；而解耦的好处，在于能够在位姿不确定的情况下，仅利用图像信息去解数据关联问题。所以直接法理应更擅长求解连续图像的定位，而特征点法则更适和全局的匹配与回环检测。读者应该明了二者优缺点的来由。

当然DSO也不是万能的。最容易看到的缺点，就是它不是个完整的SLAM——它没有回环检测、地图重用、丢失后的重定位，而这些在实际场景中往往又是必不可少的功能。DSO的初始化部分也比较慢，当然双目或RGBD相机会容易很多。如果你想要拓展DSO的功能，首先你需要十分了解DSO的代码结构。希望本文能够起到一定的作用。

资料与参考文献：

[1]. Engel J, Koltun V, Cremers D. Direct sparse odometry[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017.

[2]. Forster, C.; Pizzoli, M. & Scaramuzza, D., SVO: Fast semi-direct monocular visual odometry,Robotics and Automation (ICRA), 2014 IEEE International Conference on,2014, 15-22.

[3]. Mur-Artal, R.; Montiel, J. & Tardós, J. D. ORB-slam: a versatile and accurate monocular slam system,IEEE Transactions on Robotics, IEEE,2015, 31, 1147-1163.

[4]. Bowman, S. L.; Atanasov, N.; Daniilidis, K. & Pappas, G. J. Probabilistic data association for semantic SLAMRobotics and Automation (ICRA), 2017 IEEE International Conference on,2017, 1722-1729.

[5]. Civera, J.; Davison, A. J. & Montiel, J. M. Inverse depth parametrization for monocular SLAM,IEEE transactions on robotics, IEEE,2008, 24, 932-945.

[6]. Engel, J.; Sturm, J. & Cremers, D. Semi-dense visual odometry for a monocular cameraProceedings of the IEEE international conference on computer vision,2013, 1449-1456

[7]. 高翔, 张涛, 刘毅, 颜沁睿, 视觉SLAM十四讲：从理论与实践,电子工业出版社, 2017

[8]. Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R. & Furgale, P. Keyframe-based visual-inertial odometry using nonlinear optimizationINTERNATIONAL JOURNAL OF ROBOTICS RESEARCH,2015, 34:314-334

[9]. Barfoot, T. State Estimation for Robotics: A Matrix Lie Group Approach,Cambridge University Press,2017

[10]. SLAM中的marginalization 和 Schur complement

[11]. DSO之光度标定 - 路游侠 - 博客园

[12]高翔,知乎:半闲居士

[13]dso详解 :https://zhuanlan.zhihu.com/p/29177540

你可能感兴趣的:(V-SLAM)

V-SLAM综述：四、VINS-MONO（预积分和联合初始化）循梦渡
3——IMU预积分论文内容：1.论文第IV点的B部分IMU预积分，IMU预积分的作用是计算出IMU数据的观测值（就是IMU预积分值）以及残差的协方差矩阵和雅各比矩阵，那就要清楚的明白为什么要计算这三个量？计算出这三个量为什么就可以和视觉观测值进行耦合？如果你现在回答不出来，请好好想一想自己以前学到的知识，关于视觉的这三个量，视觉中观测值是用来计算残差的（也就是误差），残差的雅各比矩阵是优化中下降的
V-SLAM综述：一、ORB-SLAM 循梦渡
一、ORB特征ORB（OrientedFASTandRotatedBRIEF）是一种快速特征点提取和描述的算法。ORB算法分为两部分，分别是特征点提取和特征点描述。特征提取是由FAST（FeaturesfromAcceleratedSegmentTest）算法发展来的，特征点描述是根据BRIEF（BinaryRobustIndependentElementaryFeatures）特征描述算法改进的
视觉SLAM | 最小二乘优化 Way798 视觉SLAM
[1]:从零手写VIO——（三）基于优化的IMU与视觉信息融合（上篇)[2]:从零开始手写VIO第三章作业（含关键点细节及思维过程）[3]:[基础知识点]LM算法——阻尼因子更新策略(Nielsen)——内容与代码解析[4]:g2o使用总结[5]:[MVG]鲁棒估计:RANSAC&鲁棒核函数[6]:[V-SLAM]BundleAdjustment实现
[基础知识点]RANSAC+鲁棒核函数いしょ计算机视觉
目录1.RANSAC随机采样一致算法1.1相关定义1.2完整的RANSAC算法1.2.1估计模型——拟合2D直线1.2.2内点阈值ttt1.2.3采样次数NNN1.2.4内点数量阈值TTT1.3核心代码1.4实验结果2.鲁棒核函数在V-SLAM中，我们首先构造3D-3D、3D-2D、2D-2D匹配，然后据此去估计相机的运动。完美估计需要完美的匹配，但实际的匹配中往往存在很多错误。如何消除或者降低错
从零开始搭二维激光SLAM --- 基于ceres的后端优化的代码实现李太白lx 从零开始搭二维激光SLAM 优化库后端自动驾驶算法
上一篇文章我们分析了如何使用g2o进行位姿图的优化.由于g2o天然是进行位姿图优化的,所以十分契合karto的位姿图的接口,只需要将对应的顶点和约束分别赋值过去就可以了.这篇文章我们来看一下另一个比较常用的优化库Ceressolver.1ceres简介Ceressolver是谷歌开发的一款用于非线性优化的库,在激光SLAM和V-SLAM的优化中均有着大量的应用,如Cartographer,VINS
V-SLAM笔记整理总结程序猴儿 slam SLAM 视觉slam笔记 slam知识点总结 slam实习前知识总结
V-SLAM笔记整理总结参考博文：https://blog.csdn.net/qq_33414553/article/details/81270112SLAM（即时定位与建图）理解：建图：描述机器人制图Mapping时假设机器人位姿已知。制图时只需要更新地图。定位：描述机器人定位问题时假设环境地图Map已知。视觉SLAM相机种类：单目（Mono）、双目（Stereo）、深度（RGB-D）、鱼眼全景
ORBSLAM3整体框架 one to slam ORBSLAM3解读计算机视觉 slam 自动驾驶
一、前言笔者认真学习了一年半有余的SLAM，期间学习过V-SLAM、VI-SLAM、激光SLAM和激光+IMU的SLAM，在看论文和代码的闲暇之余，会时常逛知乎和CSDN等博客膜拜大佬们的文章，回顾整个过程，似乎自己没有在相关博客留下痕迹，也深刻体会到“好记性不如烂笔头”的警示作用，因此想把自己学过的东西进行总结，也抱着向大家学习的态度，文章不足之处欢迎大家批评指正。由于ORBSLAM3的SLAM
ORB-SLAM3学习：第一章--非线性最小二乘法迟暮 . 学习最小二乘法人工智能
ORB-SLAM3学习第零章–研究综述第一章–非线性最小二乘法文章目录ORB-SLAM3学习前言一、非线性最小二乘法在V-SLAM算法中的应用和简单理解1.1在V-SLAM中的简单说明1.2最小二乘法的简单引入二、牛顿公式推导2.1一维函数求最小值2.2二（多）维函数求最小值二、高斯--牛顿公式推导2.1基础知识2.2抛出问题2.3优化目标函数总结前言视觉SLAM中后端优化使用了诸多算法，非线性最
关于视觉SLAM的最先进技术的调查-A survey of state-of-the-art on visual SLAM Alaso_soso 论文阅读笔记 VSLAM 机器学习计算机视觉人工智能
原文见文章末尾：今天读了一篇视觉slam的综述，真的是读了一天，记录一下。我比较关注的是特征提取和匹配和深度学习有关的章节。好久，但是还算是有收获的吧。摘要：本文概述了视觉同步定位和测绘（V-SLAM）。我们讨论了SLAM和视觉系统领域的基本定义，并对用于移动机器人视觉和SLAM的最先进方法进行了回顾。本文涵盖了基本的SLAM方法、视觉传感器、用于特征提取和匹配的机器视觉算法、深度学习（DL）方法
python点云快速配准_分享一个V-SLAM中点云配准算法改进的方法 weixin_39617484 python点云快速配准
近年来，随着自主导航的广泛应用，视觉同时定位与地图构建(Visualsimultaneouslocalizationandmapping,V-SLAM)通过自身携带的视觉传感器对周围环境进行重构并且估计出自身的位置，准确定位与高精度的V-SLAM算法是实现自主导航的关键技术。V-SLAM一般分为前端视觉部分和优化的后端部分基于特征点法的前端视觉部分，一直以来都是视觉里程计(VisualOdomet
V-SLAM综述：基础（问答和名词解释）循梦渡
面经问题集：https://blog.csdn.net/weixin_43795395/article/details/89762278基础矩阵F、本质矩阵E、单应矩阵H的理解和推导：（至关重要）https://www.zhihu.com/question/27581884/answer/105606049单目相机，F和H矩阵有何不同，E和F矩阵有何不同E：本质矩阵F：基本矩阵H：单应矩阵E=t*
【AR实验室】OpenGL ES绘制相机（OpenGL ES 1.0版本）（转）树上的cat_ee3c
转自：http://www.cnblogs.com/polobymulberry/p/6130376.html之前做一些移动端的AR应用以及目前看到的一些AR应用，基本上都是这样一个套路：手机背景显示现实场景，然后在该背景上进行图形学绘制。至于图形学绘制时，相机外参的解算使用的是V-SLAM、Marker-Based还是GPS的方法，就不一而足了。所以说要在手机上进行现实场景的展现也是目前AR应用
我是怎么从0开始跑通ORBSLAM2+kinectv1的（win8或者win10） qq184861643 SLAM
我在研0阶段接到的实验室的第一个项目，是和本校的另外一个实验室的合作项目，分给我的第一阶段的任务是对一个简单的室内环境进行三维重建。经过一些自己的调研和向一位远在日本从事SLAM研究的老师的请教，最后决定用V-SLAM的方法来实现第一阶段的任务。经过一段时间的钻研，我个人决定用ORBSLAM2。因为整个项目从头到尾都是我一个人做，摸索了很多，进了很多坑，最后终于跑通了，决定把这整个过程记录下来。我
基于单目视觉的同时定位与地图构建方法综述 chenying66 SLAM
主要针对增强现实的应用场景。指出AR需要实时定位设备在环境中的方位。定位方案虽然已经有很多种，但多数方案要么在实际应用中存在诸多局限，要么代价太高难以普及。背景在AR应用中，由于虚拟物体的叠加目标通常为图像、视频，因此基于图像、视频等视觉信息的V-SLAM方案，对于确保虚实融合效果在几何上保持一致有着天然的优势。主要针对单目相机的V-SLAMV-SLAM的目标:同时恢复出每帧图像对应的相机运动参数
工作总结（2018.6.19-2018.6.22） teddyluo
上周已完成的工作（2018.6.19-2018.6.22）学习吴教授strategiesplanning参加小组月度和半年工作总结会参加华中科大钟胜副院长《成像实时自动目标识别及其应用》讲座小组基础学习讨论会v-slam:对极几何、三角测量、PnP、BundleAdjustment、ICP的初步学习本周工作计划（2018.6.25-2018.6.29）v-slam:对极几何、三角测量、PnP、Bu
V-SLAM 回环检测与后端优化重读爱发呆de白菜头创建和维护自己的SLAM系统 g2o 回环检测 vSLAM
研究背景：后端优化原理大多人都比较清楚，但是实现起来不是个容易的事情，而回环检测部分在自己测试之后发现，这部分在vSLAM中也是至关重要的，本文的给出了在没有好的回环下得到的地图样例。1.几个坏的回环结果2.问题描述误差积累：相机转过去的过程正常运行，但转回来时会出现明显偏差;点云重建效率：在线点云更新速度较慢,不实时显示速度影响不大.3.VO－视觉里程计的问题帧----帧，匹配获取相机位姿相邻帧
Enum 枚举 120153216 enum 枚举
原文地址：http://www.cnblogs.com/Kavlez/p/4268601.html Enumeration 于Java 1.5增加的enum type...enum type是由一组固定的常量组成的类型，比如四个季节、扑克花色。在出现enum type之前，通常用一组int常量表示枚举类型。比如这样： public static final int APPLE_FUJI = 0
Java8简明教程 bijian1013 java jdk1.8
Java 8已于2014年3月18日正式发布了，新版本带来了诸多改进，包括Lambda表达式、Streams、日期时间API等等。本文就带你领略Java 8的全新特性。一.允许在接口中有默认方法实现 Java 8 允许我们使用default关键字，为接口声明添
Oracle表维护快速备份删除数据 cuisuqiang oracle 索引快速备份删除
我知道oracle表分区，不过那是数据库设计阶段的事情，目前是远水解不了近渴。当前的数据库表，要求保留一个月数据，且表存在大量录入更新，不存在程序删除。为了解决频繁查询和更新的瓶颈，我在oracle内根据需要创建了索引。但是随着数据量的增加，一个半月数据就要超千万，此时就算有索引，对高并发的查询和更新来说，让然有所拖累。为了解决这个问题，我一般一个月会进行一次数据库维护，主要工作就是备
java多态内存分析麦田的设计者 java 内存分析多态原理接口和抽象类
“ 时针如果可以回头，熟悉那张脸，重温嬉戏这乐园，墙壁的松脱涂鸦已经褪色才明白存在的价值归于记忆。街角小店尚存在吗？这大时代会不会牵挂，过去现在花开怎么会等待。但有种意外不管痛不痛都有伤害，光阴远远离开，那笑声徘徊与脑海。但这一秒可笑不再可爱，当天心
Xshell实现Windows上传文件到Linux主机被触发 windows
经常有这样的需求，我们在Windows下载的软件包，如何上传到远程Linux主机上？还有如何从Linux主机下载软件包到Windows下；之前我的做法现在看来好笨好繁琐，不过也达到了目的，笨人有本方法嘛；我是怎么操作的： 1、打开一台本地Linux虚拟机，使用mount 挂载Windows的共享文件夹到Linux上，然后拷贝数据到Linux虚拟机里面；（经常第一步都不顺利，无法挂载Windo
类的加载ClassLoader 肆无忌惮_ ClassLoader
类加载器ClassLoader是用来将java的类加载到虚拟机中，类加载器负责读取class字节文件到内存中，并将它转为Class的对象（类对象），通过此实例的 newInstance()方法就可以创建出该类的一个对象。其中重要的方法为findClass(String name)。如何写一个自己的类加载器呢？首先写一个便于测试的类Student
html5写的玫瑰花知了ing html5
<html> <head> <title>I Love You!</title> <meta charset="utf-8" /> </head> <body> <canvas id="c"></canvas>
google的ConcurrentLinkedHashmap源代码解析矮蛋蛋 LRU
原文地址： http://janeky.iteye.com/blog/1534352 简述 ConcurrentLinkedHashMap 是google团队提供的一个容器。它有什么用呢？其实它本身是对 ConcurrentHashMap的封装，可以用来实现一个基于LRU策略的缓存。详细介绍可以参见 http://code.google.com/p/concurrentlinke
webservice获取访问服务的ip地址 alleni123 webservice
1. 首先注入javax.xml.ws.WebServiceContext, @Resource private WebServiceContext context; 2. 在方法中获取交换请求的对象。 javax.xml.ws.handler.MessageContext mc=context.getMessageContext(); com.sun.net.http
菜鸟的java基础提升之道——————>是否值得拥有百合不是茶
1，c++，java是面向对象编程的语言，将万事万物都看成是对象；java做一件事情关注的是人物，java是c++继承过来的，java没有直接更改地址的权限但是可以通过引用来传值操作地址，java也没有c++中繁琐的操作，java以其优越的可移植型，平台的安全型，高效性赢得了广泛的认同，全世界越来越多的人去学习java，我也是其中的一员 java组成：
通过修改Linux服务自动启动指定应用程序 bijian1013 linux
Linux中修改系统服务的命令是chkconfig (check config)，命令的详细解释如下: chkconfig 功能说明：检查，设置系统的各种服务。语　　法：chkconfig [ -- add][ -- del][ -- list][系统服务] 或 chkconfig [ -- level <</SPAN>
spring拦截器的一个简单实例 bijian1013 java spring 拦截器 Interceptor
Purview接口 package aop; public interface Purview { void checkLogin(); } Purview接口的实现类PurviesImpl.java package aop; public class PurviewImpl implements Purview { public void check
[Velocity二]自定义Velocity指令 bit1129 velocity
什么是Velocity指令在Velocity中，#set,#if, #foreach, #elseif, #parse等，以#开头的称之为指令，Velocity内置的这些指令可以用来做赋值，条件判断，循环控制等脚本语言必备的逻辑控制等语句，Velocity的指令是可扩展的，即用户可以根据实际的需要自定义Velocity指令自定义指令(Directive)的一般步骤 &nbs
【Hive十】Programming Hive学习笔记 bit1129 programming
第二章 Getting Started 1.Hive最大的局限性是什么？一是不支持行级别的增删改(insert, delete, update)二是查询性能非常差(基于Hadoop MapReduce）,不适合延迟小的交互式任务三是不支持事务2. Hive MetaStore是干什么的？Hive persists table schemas and other system metadata.
nginx有选择性进行限制 ronin47 nginx 动静　限制
http { limit_conn_zone $binary_remote_addr zone=addr:10m; limit_req_zone $binary_remote_addr zone=one:10m rate=5r/s;... server {... location ~.*\.(gif|png|css|js|icon)$ {
java-4.-在二元树中找出和为某一值的所有路径 . bylijinnan java
/* * 0.use a TwoWayLinkedList to store the path.when the node can't be path,you should/can delete it. * 1.curSum==exceptedSum:if the lastNode is TreeNode,printPath();delete the node otherwise
Netty学习笔记 bylijinnan java netty
本文是阅读以下两篇文章时： http://seeallhearall.blogspot.com/2012/05/netty-tutorial-part-1-introduction-to.html http://seeallhearall.blogspot.com/2012/06/netty-tutorial-part-15-on-channel.html 我的一些笔记 ===
js获取项目路径 cngolon js
//js获取项目根路径，如： http://localhost:8083/uimcardprj function getRootPath(){ //获取当前网址，如： http://localhost:8083/uimcardprj/share/meun.jsp var curWwwPath=window.document.locati
oracle 的性能优化 cuishikuan oracle SQL Server
在网上搜索了一些Oracle性能优化的文章，为了更加深层次的巩固[边写边记]，也为了可以随时查看，所以发表这篇文章。 1.ORACLE采用自下而上的顺序解析WHERE子句，根据这个原理，表之间的连接必须写在其他WHERE条件之前，那些可以过滤掉最大数量记录的条件必须写在WHERE子句的末尾。（这点本人曾经做过实例验证过，的确如此哦！
Shell变量和数组使用详解 daizj linux shell 变量数组
Shell 变量定义变量时，变量名不加美元符号（$，PHP语言中变量需要），如： your_name="w3cschool.cc" 注意，变量名和等号之间不能有空格，这可能和你熟悉的所有编程语言都不一样。同时，变量名的命名须遵循如下规则：首个字符必须为字母（a-z，A-Z）。中间不能有空格，可以使用下划线（_）。不能使用标点符号。不能使用ba
编程中的一些概念，KISS、DRY、MVC、OOP、REST dcj3sjt126com REST
KISS、DRY、MVC、OOP、REST （1）KISS是指Keep It Simple,Stupid（摘自wikipedia），指设计时要坚持简约原则，避免不必要的复杂化。（2）DRY是指Don't Repeat Yourself（摘自wikipedia），特指在程序设计以及计算中避免重复代码，因为这样会降低灵活性、简洁性，并且可能导致代码之间的矛盾。（3）OOP 即Object-Orie
[Android]设置Activity为全屏显示的两种方法 dcj3sjt126com Activity
1. 方法1：AndroidManifest.xml 里，Activity的 android:theme 指定为" @android:style/Theme.NoTitleBar.Fullscreen" 示例: <application
solrcloud 部署方式比较 eksliang solrCloud
solrcloud 的部署其实有两种方式可选，那么我们在实践开发中应该怎样选择呢？第一种：当启动solr服务器时，内嵌的启动一个Zookeeper服务器，然后将这些内嵌的Zookeeper服务器组成一个集群。第二种：将Zookeeper服务器独立的配置一个集群，然后将solr交给Zookeeper进行管理谈谈第一种：每启动一个solr服务器就内嵌的启动一个Zoo
Java synchronized关键字详解 gqdy365 synchronized
转载自：http://www.cnblogs.com/mengdd/archive/2013/02/16/2913806.html 多线程的同步机制对资源进行加锁，使得在同一个时间，只有一个线程可以进行操作，同步用以解决多个线程同时访问时可能出现的问题。同步机制可以使用synchronized关键字实现。当synchronized关键字修饰一个方法的时候，该方法叫做同步方法。当s
js实现登录时记住用户名 hw1287789687 记住我记住密码 cookie 记住用户名记住账号
在页面中如何获取cookie值呢? 如果是JSP的话,可以通过servlet的对象request 获取cookie,可以参考:http://hw1287789687.iteye.com/blog/2050040 如果要求登录页面是html呢?html页面中如何获取cookie呢? 直接上代码了页面:loginInput.html 代码: <!DOCTYPE html PUB
开发者必备的 Chrome 扩展 justjavac chrome
Firebug：不用多介绍了吧https://chrome.google.com/webstore/detail/bmagokdooijbeehmkpknfglimnifench ChromeSnifferPlus：Chrome 探测器，可以探测正在使用的开源软件或者 js 类库https://chrome.google.com/webstore/detail/chrome-sniffer-pl
算法机试题李亚飞 java 算法机试题
在面试机试时，遇到一个算法题，当时没能写出来，最后是同学帮忙解决的。这道题大致意思是：输入一个数，比如4,。这时会输出： &n
正确配置Linux系统ulimit值字符串 ulimit
在Linux下面部署应用的时候，有时候会遇上Socket/File: Can’t open so many files的问题；这个值也会影响服务器的最大并发数，其实Linux是有文件句柄限制的，而且Linux默认不是很高，一般都是1024，生产服务器用其实很容易就达到这个数量。下面说的是，如何通过正解配置来改正这个系统默认值。因为这个问题是我配置Nginx+php5时遇到了，所以我将这篇归纳进
hibernate调用返回游标的存储过程 Supanccy2013 java DAO oracle Hibernate jdbc
注：原创作品，转载请注明出处。上篇博文介绍的是hibernate调用返回单值的存储过程，本片博文说的是hibernate调用返回游标的存储过程。此此扁博文的存储过程的功能相当于是jdbc调用select 的作用。 1，创建oracle中的包，并在该包中创建的游标类型。 ---创建oracle的程
Spring 4.2新特性-更简单的Application Event wiselyman application
1.1 Application Event Spring 4.1的写法请参考10点睛Spring4.1-Application Event 请对比10点睛Spring4.1-Application Event 使用一个@EventListener取代了实现ApplicationListener接口,使耦合度降低; 1.2 示例包依赖 <p