李航《统计学习方法》——第五章决策树及Python实现(附习题答案)
文章目录
- 1 模型
- 2 策略
- 3 算法
- 3.1 ID3 算法(C4.5算法)决策树
- 3.1.1 特征选择
- ID3 算法
- C4.5算法
- 3.1.2 决策树生成
- 3.2 CART(回归树和决策树)
- 3.2.1 特征选择
- 3.2.1.1 回归——最小二乘
- 3.2.1.2 模型树——最小化线性方程误差
- 3.2.1.3 决策——基尼系数
- 3.2.2 回归树/决策树生成
- 3.2.3 剪枝
- 预剪枝
- 后剪枝
- 3.2.4 分类
- 4 总结
- 优点
- 缺点:
- 5 习题
- 5.1 利用信息增益比生层决策树
- 5.2 平方误差生成回归树
先感叹一下,C++水平真的差啊~~~~人生苦短,我用Python
决策树是一种基本的分类与回归模型,呈树形结构。可以看作if-then的处理结构,也可以看作条件概率分布,对特征空间进行划分,在子特征空间进行类别判断,大于阈值则属于子空间的类别。

1 模型
由结点和有向边组成,结点有两种类型,内部结点和叶结点
分类模型 :内部结点表示一个特征或者一个属性
叶节点表示一个类——每个结点的样本可能很多,可使用多数投票进行判断
回归模型:内部节点表示划分的值,也相当于属性
叶结点表示预测结果——样本到达叶结点预测结果的判定,可采用所有叶结点的均值
《机器学习实战》第九章介绍,样本到达叶节点,也可以对叶结点的样本采用构造回归模型进行处理,这样可 以回归模型可以针对数据生成不同的回归函数(分段),拟合效果更好
2 策略
正则化的最大似然函数【拟合程度+模型复杂度(叶子结点的个数)】
模型复杂度是为防止过拟合的剪枝过程
3 算法
- 特征选择:回归问题——最小二乘
分类问题——信息增益——>算法ID3
——信息增益比——>算法C4.5
——基尼系数——>算法CART - 决策树生成
- 剪枝 预剪枝和后剪枝
3.1 ID3 算法(C4.5算法)决策树
3.1.1 特征选择
ID3 算法
信息增益
表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
特征A对训练数据集D的信息增益记为 g ( D , A ) g(D,A) g(D,A),集合D的信息熵为 H ( D ) H(D) H(D),给定特征A时集合D的条件经验熵记为 H ( D ∣ A ) H(D|A) H(D∣A),则信息增益就等于 g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A) = H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)其中 H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ l o g 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K}\frac{|C_k|}{|D|}log_2\frac{|C_k|}{|D|} H(D)=−∑k=1K∣D∣∣Ck∣log2∣D∣∣Ck∣[ ∣ C k ∣ |C_k| ∣Ck∣表示样本中每一类的个数 ∣ D ∣ |D| ∣D∣表示总样本数]
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ l o g 2 ∣ D i k ∣ ∣ D i ∣ H(D|A) = \sum_{i=1}^{n}\frac{|D_i|}{|D|}H(D_i)=-\sum_{i=1}^{n}\frac{|D_i|}{|D|}\sum_{k=1}^{K}\frac{|D_{ik}|}{|D_i|}log_2\frac{|D_{ik}|}{|D_i|} H(D∣A)=∑i=1n∣D∣∣Di∣H(Di)=−∑i=1n∣D∣∣Di∣∑k=1K∣Di∣∣Dik∣log2∣Di∣∣Dik∣[ n n n表示根据特征A将D可以划分为几个数据集, ∣ D i ∣ |D_i| ∣Di∣为每个数据集样本的个数,相加等于 ∣ D ∣ |D| ∣D∣。 D i k D_{ik} Dik表示对每一个以特征A划分的子数据集中划分类别,然后求熵——也就是对每一个以特征A划分的子数据集求经验熵,然后计算加权和]
因此对框架的构造很重要,首先需要有根据特征对数据集进行划分的函数,然后对计算一个集合的熵。一开始对公式的理解不到位,直接按H(D|A)的公式计算,十分的麻烦-----
Python实现,首先根据某个特征的某个取值进行数据集划分成其特征值个子集。
'''
按照特定特征划分数据集,axis 特征的维度,value 特征的值
'''
def splitDataSet(dataSet,axis,value):
retDataSet = []
for featvec in dataSet:
if featvec[axis] == value:
#一下两句,是将这个特征去除了
reduceFeatVec = featvec[:axis]
reduceFeatVec.extend(featvec[axis+1:])
retDataSet.append(reduceFeatVec)
return retDataSet
#计算数据集的熵
def calEntropy(dataSet,feature =-1):
#增加一个feature参数,默认 -1,也就是计算最后一列类别的熵
#如果改变数值,可以计算信息增益比中,数据集D关于每个特征的经验熵
numSamples = len(dataSet)
labelCounts = {}
#根据样本标签计算每一类的样本个数
for featVec in dataSet:
currentLabel = featVec[feature]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
Entropy = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numSamples
Entropy = Entropy - prob*log(prob,2)
return Entropy
ID3算法存在的问题:
- ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现,在相同条件下,取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值,各为1/2,另一个变量为3个值,各为1/3,其实他们都是完全不确定的变量,但是取3个值的比取2个值的信息增益大。如果校正这个问题呢?
C4.5算法
信息增益比
针对利用信息增益计算要选择的特征会会偏重选择特征值较多的特征的问题,利用数据集D关于特征A取值 的熵 H A ( D ) H_A(D) HA(D)进行校正。 g R ( D , A ) = g ( D , A ) H A ( D ) g_R(D,A) = \frac{g(D,A)}{H_A(D)} gR(D,A)=HA(D)g(D,A)其中 H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ l o g 2 ∣ D i ∣ ∣ D ∣ H_A(D) = -\sum_{i=1}^{n}\frac{|D_i|}{|D|}log_2\frac{|D_i|}{|D|} HA(D)=−∑i=1n∣D∣∣Di∣log2∣D∣∣Di∣, n n n是特征A取值的个数。
针对这一改变,将数据集D关于特征A的熵进行计算。
#计算单个特征的熵
def calFeatureEntropy(dataSet):
numSamples = len(dataSet)
featureCounts = {}
featureEntropy = []
for i in range(len(dataSet[0])-1):
Entropy = calEntropy(dataSet,feature=i)
featureEntropy.append(Entropy)
return featureEntropy
以上是针对不同的算法得到不同的特征重要性衡量方法,接下来就要根据计算来选择最好的特征了。无论是信息增益还是信息增益比,都是一个寻找最大的值的过程,也就是如果满足得到的信息增益比baseInfoGain 大就就变换baseInfoGain 。
'''
使用信息增益计算最好的特征,返回特征列的索引
这实现起来很有意思啊
info 计算条件尚的方法,默认id3,也可以设置为C54
'''
def chosseBestFeatureToSplit(dataSet,info ='id3'):
numFeatures = len(dataSet[0])-1
if info == 'id3':
featureEntropy = ones((numFeatures ,1))
elif info =='c54':
featureEntropy = calFeatureEntropy(dataSet)
baseEntropy = calEntropy(dataSet)
baseInfoGain = 0.0
baseFeature = -1
for i in range(numFeatures):
#我靠,这比C++简单多了
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) #用set创建无序不重复集合
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob*calEntropy(subDataSet)
infoGain = baseEntropy - newEntropy
infoGain = infoGain/featureEntropy[i]
if(infoGain>baseInfoGain):
baseInfoGain = infoGain
baseFeature = i
return baseFeature
3.1.2 决策树生成
输入:训练数据集D,特征集A [实现的时候没有使用:阈值 ϵ \epsilon ϵ ]
输出:决策树T
[1]. 若D中所有实例属于同一类 C k C_k Ck,则 T T T为单节点树,并将类 C k C_k Ck作为该点的类标记,返回 T T T
[2]. 若A= ∅ \emptyset ∅,则 T T T为单节点树,并将D中实例数最大的类 C k C_k Ck作为该节点的类标记,返回T
[3]. 否则计算各个特征对数据集D的信息增益(比),选择信息增益(比)最大的特征 A g A_g Ag
[4]. 如果 A g A_g Ag的信息增益小于阈值 ϵ \epsilon ϵ,则置T为单结点树,并将D中实例数最大的类 C k C_k Ck作为该节点的类标记,返回T
[5]. 否则,对 A g A_g Ag的每一种可能值 a i a_i ai,依 A g = a i A_g=a_i Ag=ai将D分割为若干非空子集 D i D_i Di,将 D i D_i Di中实例数最大的类作为类标记,构建子节点,由结点及其子节点构成树T,返回T
[6]. 对第 i i i个子节点,以 D i D_i Di为训练集,以 A − A g A-{A_g} A−Ag为特征集,递归调用前面五步,得到 T i T_i Ti,返回 T i T_i Ti
据算法步骤使用python实现,参考了《机器学习实战》,并有一些细微改动。
''' 多数表决,classCount,字典,按照标签存储每个标签预测的个数 '''
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
#operator.itemgetter(1) 选择第一个域的值 相当于定义了一个函数
#sorted可以对list或者iterator进行排序 true降序排列
sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True)
return sortedClassCount[0][0]
def createTree(dataSet,labels,info = 'id3'):
classList = [example[-1] for example in dataSet]
#如果都是一类则 返回这一类作为类标签 第[1]步
if classList.count(classList[0]) == len(classList):
return classList[0]
# 所有的特征都进行过分支,只剩下类别列,进行投票判决[$A=\emptyset$] 第[2]步
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择信息增益最大的特征,返回的是特征的序号 第[3]步
bestFeat = chosseBestFeatureToSplit(dataSet,info)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}} #递归构造树
del(labels[bestFeat])
'''第[5]步 及 第[6]步,计算特征每个取值的集,构建子结点,然后递归前面几步构造树
没有对阈值的计算,如果计算的话,可以在chosseBestFeatureToSplit()设置阈值,如果小于阈值,
返回一个特征标号和一个标志,然后构造单节点树即可'''
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
return myTree
这两个算法的实现没有采用剪枝,所以这里贴出完整代码,所用数据集都是《机器学习实战》中附加的。
# -*- coding: utf-8 -*-
''' Created on Oct 12, 2010 Decision Tree Source Code for Machine Learning in Action Ch. 3 @author: Li '''
from math import log
import operator
import treePlotter
def CreatDataSet():
dataSet = [[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]
labels = ['no surfacing','flippers']
return dataSet,labels
def calEntropy(dataSet):
def calFeatureEntropy(dataSet):
def splitDataSet(dataSet,axis,value):
def chosseBestFeatureToSplit(dataSet,info ='id3'):
def majorityCnt(classList):
def createTree(dataSet,labels,info = 'id3'):
''' 不是C++ 指针实现意义上的树,使用Python字典实现,嵌套字典结构存储树结构 递归查找树,到节点为止 '''
def classify(inputTree,featLabels,testVec):
firstStr = inputTree.keys()[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key],featLabels,testVec)
else:
classLabel = secondDict[key]
return classLabel ##存储树结构
def storeTree(inputTree,fileName):
import pickle
fw = open(fileName,'w')
pickle.dump(inputTree,fw)
fw.close()
##加载树结构
def loadTree(fileName):
import pickle
fr = open(fileName)
return pickle.load(fr)
def main():
fr = open('lenses.txt')
lense = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels = ['age','prescript','astigmatic','tearRate']
lenseTree = createTree(lense,lensesLabels,info='c54')
treePlotter.createPlot(lenseTree)
return lense
if __name__ == "__main__":
lense = main()
3.2 CART(回归树和决策树)
ID3等不能处理连续型数据,只能事先将连续型变量处理成离散型,才可以。CART假设决策树是二叉树,等价于递归二分每个特征,因此能够便于处理连续数据,即可用于回归又可用于分类。
【区别,最主要的根据特征二分数据集,因此需要选择好特征和特征值,也就是特征选择会发生变化】
3.2.1 特征选择
下面根据统计学习方法,及机器学习实战,实现了分类回归树的三种叶子节点计算方式和误差计算方法。
3.2.1.1 回归——最小二乘
寻找最优切分变量 j j j和最优切分点 s s s ,第 j j j个切分变量 x ( j ) x^{(j)} x(j)和其取值将数据集划分为两个集合 R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } R 2 ( j , s ) = { x ∣ x ( j ) > s } R_1(j,s) = \{x|x^{(j)} \le s\} \quad R_2(j,s) = \{x|x^{(j)} > s\} R1(j,s)={x∣x(j)≤s}R2(j,s)={x∣x(j)>s} c i c_i ci表示划分到叶子结点时,如果取叶子结点的值,这里采用平均值,即 c i = a v e ( y i ∣ x i ∈ R m ) c_i = ave(y_i|x_i\in R_m) ci=ave(yi∣xi∈Rm)
m i n j , s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] min_{j,s}[min_{c_1}\sum_{x_i \in R_1(j,s)}(y_i-c_1)^2+min_{c_2}\sum_{x_i \in R_2(j,s)}(y_i-c_2)^2] minj,s[minc1xi∈R1(j,s)∑(yi−c1)2+minc2xi∈R2(j,s)∑(yi−c2)2]
'''
叶子节点的计算方式,在回归问题中为叶子节点值的均值
'''
def regLeaf(dataSet):
return mean(dataSet[:,-1])
'''
如果是回归问题,误差为最小均方误差
使用var计算,最后乘以样本个数
'''
def regErr(dataSet,n):
return var(dataSet[:,-1])*dataSet.shape[0]
3.2.1.2 模型树——最小化线性方程误差
与上面普通回归树相似,只是划分到叶子结点时 c i c_i ci的计算方式改变了
线性回归方程为 y i = x i ∗ w + b x i ∈ R m y_i = x_i*w+b x_i \in R_m yi=xi∗w+bxi∈Rm ,为方便计算将 w , b w,b w,b吸收如向量形式 w s = ( w ; b ) ws = (w;b) ws=(w;b),而 x i x_i xi扩展为第一列全为1,则 y i = x i ∗ w s y_i = x_i*ws yi=xi∗ws。 w s ∗ = a r g m a x w s ( y − x ∗ w s ) T ( y − x ∗ w s ) ws^* = argmax_{ws}(y-x*ws)^T(y-x*ws) ws∗=argmaxws(y−x∗ws)T(y−x∗ws)对误差函数求导并使之等于0,可以解得 w s ∗ = ( x T x ) − 1 x T y ws^* = (x^Tx)^{-1}x^Ty ws∗=(xTx)−1xTy,前提是 x T x x^Tx xTx是满秩矩阵,现实中如果列数大于行数会有很多解,需要引入正则化。
求解完,最终的回归模型为 f ( x i ) = x ‾ i T ∗ ( x T x ) − 1 x T y f(x_i) = \overline{x}_i^T*(x^Tx)^{-1}x^Ty f(xi)=xiT∗(xTx)−1xTy,以下为按照思路求解的Python代码。
def linearSolve(dataSet):
m,n = shape(dataSet)
X= mat(ones((m,n)))
Y = mat(ones((m,1)))
X[:,1:n] = dataSet[:,0:n-1];Y = dataSet[:,-1]
xXx = X.T*X
if linalg.det(xXx) == 0.0:
raise NameError('This matrix is singular, cannot do inverse,\n\ try increasing the second value of ops ')
ws = xXx.T*(X.T*Y)
return ws,X,Y
def modelLeaf(dataSet):
ws,X,Y= linearSolve(dataSet)
return ws
def modelErr(dataSet,n):
ws,X,Y = linearSolve(dataSet)
y_pred = X*ws
return sum(power(y_pred-Y,2))
3.2.1.3 决策——基尼系数
对于样本集合D, G i n i = 1 − ∑ k = 1 K ( ∣ C k ∣ ∣ D ∣ ) 2 Gini = 1- \sum_{k=1}^{K}(\frac{|C_k|}{|D|})^2 Gini=1−∑k=1K(∣D∣∣Ck∣)2
在给定特征A条件下,对于某一个特征值划分的两个集合,集合D的基尼指数定义为: G i n i ( D , A ) = ∣ D 1 ∣ ∣ D ∣ G i n i ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ G i n i ( D 2 ) Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1)+ \frac{|D_2|}{|D|}Gini(D_2) Gini(D,A)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)基尼指数越大,样本集合的不确定性也就越大。
'''
分类问题叶子节点和误差计算
'''
#多数表决
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
#operator.itemgetter(1) 选择第一个域的值 相当于定义了一个函数
#sorted可以对list或者iterator进行排序 true降序排列
sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True)
return sortedClassCount[0][0]
def classLeaf(dataSet):
#基于多数投票,判断节点叶子的类别
classList = dataSet[:,-1].T.tolist()[0]
return majorityCnt(classList)
#回归问题采用最小均方误差,分类问题使用基尼系数判断
def classErr(dataSet,n):
C= list(set(dataSet[:,-1].T.tolist()[0]))
classes = len(set(dataSet[:,-1].T.tolist()[0]))
samples = len(dataSet[:,-1])
ck =[sum((dataSet[:,-1] == C[i])==True) for i in range(classes)]
temp = array(ck)/samples
gini = 1 - sum(power(temp,2))
return (gini)*samples/n
————————————————————————————————————————————————————————
与3.1节一样,为了方便计算,首先封装一个二分数据集的函数,然后再结合上述增益计算方法,选择最好的特征以及划分值。
划分数据集
'''
既可以用于回归问题,也可以用于分类问题
二分数据集
'''
def binSplitDataSet(dataSet,feature,value):
mat0 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:]
mat1 = dataSet[nonzero(dataSet[:,feature] >value)[0],:]
return mat(mat0),mat(mat1)
选择最优特征进行划分
根据不同的特征选择及误差计算方式,以及停止条件,计算最优特征,并返回特征索引,及最优划分的值
'''
选择最好的特征及划分点,
'''
def chooseBestToSplit(dataSet,leafType = regLeaf,errType = regErr,ops = (1,4)):
#提前结束标志
tolS = ops[0]; tolN = ops[1]
if len(set(dataSet[:,-1].T.tolist()[0]))==1:
return None ,leafType(dataSet)
m,n = dataSet.shape
S = errType(dataSet,m)
bestS = inf
bestFeature = 0
bestValue = 0
for featvec in range(n-1):
for val in set(dataSet[:,featvec].T.tolist()[0]):
mat0,mat1 = binSplitDataSet(dataSet,featvec,val)
if (mat0.shape[0]<tolN) or (mat1.shape[0]<tolN):
continue
newS = errType(mat0,m)+errType(mat1,m)
if newS < bestS:
bestFeature = featvec
bestValue = val
bestS = newS
if (S-bestS)<tolS:
return None,leafType(dataSet)
mat0 , mat1 = binSplitDataSet(dataSet,bestFeature,bestValue)
if (mat0.shape[0]<tolN) or (mat1.shape[0]<tolN):
return None,leafType(dataSet)
return bestFeature,bestValue
3.2.2 回归树/决策树生成
输入:训练数据集,叶子结点计算方式,叶子结点误差计算方式,停止条件
输出:回归或者分类树T
在训练数据集所在的输入空间中,递归地将每个区域划分为两个子区域并决
定每个子区域上的输出值,构建二叉决策树:
- [1] 选择最优切分点和最优切分变量,计算方式如特征选择所示
- [2] 用选定的特征及划分值,划分数据集,并计算输出值
- [3] 递归调用前两步
'''
递归构造树结构
'''
def createTree(dataSet,leafType = regLeaf,errType = regErr,ops=(1,4)):
# 第[1]步
feature ,value = chooseBestToSplit(dataSet,leafType,errType,ops)
if feature ==None: return value
retTree = {}
retTree['spInd'] = feature
retTree['spVal'] = value
#第[2]步
lSet,rSet = binSplitDataSet(dataSet,feature,value)
#第[3]步
retTree['left'] = createTree(lSet,leafType,errType,ops)#mat0
retTree['right'] = createTree(rSet,leafType,errType,ops)
return retTree
3.2.3 剪枝
预剪枝
ops参数为树生成停止条件,改变参数的值,可以在树生成的时候就减少结点个数,减少拟合。
后剪枝
CART回归树和CART分类树的剪枝策略除了在度量损失的时候一个使用均方差,一个使用基尼系数,算法基本完全一样。
由于决策时算法很容易对训练集过拟合,而导致泛化能力差,为了解决这个问题,我们需要对CART树进行剪枝,即类似于线性回归的正则化,来增加决策树的泛化能力。但是,有很多的剪枝方法,我们应该这么选择呢?CART采用的办法是后剪枝法,即先生成决策树,然后产生所有可能的剪枝后的CART树,然后使用交叉验证来检验各种剪枝的效果,选择泛化能力最好的剪枝策略。
也就是说,CART树的剪枝算法可以概括为两步,第一步是从原始决策树生成各种剪枝效果的决策树,第二部是用交叉验证来检验剪枝后的预测能力,选择泛化预测能力最好的剪枝后的数作为最终的CART树。
机器学习实战中采用递归子树到叶子结点,如果合并的误差小于单节点的误差,则合并两个结点,这里只针对回归实现,未实现其他函数。
#%% 剪枝
def isTree(obj):
return (type(obj).__name__ == 'dict')
def getMean(tree):
if isTree(tree['right']): tree['right'] = getMean(tree['right'])
if isTree(tree['left']): tree['left'] = getMean(tree['left'])
return (tree['right']+tree['left'])/2.0
def prune(tree,testData):
#如果没有测试数据,返回树的均值
if testData.shape[0] == 0: return getMean(tree)
if isTree(tree['right']) or isTree(tree['left']):
lSet,rSet = binSplitDataSet(testData,tree['spInd'],tree['spVal'])
if isTree(tree['right']): tree['right'] = prune(tree['right'],rSet)
if isTree(tree['left']): tree['left'] = prune(tree['left'],lSet)
if not isTree(tree['right']) and not isTree(tree['left']):
lSet,rSet = binSplitDataSet(testData,tree['spInd'],tree['spVal'])
####################################机器学习实战针对回归树对合并后和合并前的均方差进行计算,这里可以封装成根据任务计算的函数
errorMoMerge = sum(power(lSet[:,-1]-tree['left'],2))+sum(power(rSet[:,-1]-tree['right'],2))
treeMean = (tree['right']+tree['left'])/2.0
errorMerge = sum(power(testData[:-1]-treeMean,2))
####################################
if errorMerge<errorMoMerge:
print('merging')
return treeMean
else:
return tree
return tree
3.2.4 分类
#%% 用回归树进行预测
#回归
def regTreeEval(model,inDat):
return model
#模型构造 只有回归模型在最后预测的时候需要输入数据,因为回归模型的叶子节点保存的是叶子节点回归函数的系数,需要根据输入数据进行预测
def modelTreeEval(model,inDat):
n = inDat.shape[1]
x = mat(ones((1,n+1)))
x[:,1:n+1] = inDat
return float(x*model)
#分类问题
def classTreeEval(model,inDat):
return model
#单个数据预测
def treeForeCast(tree,inDat,modelEval=regTreeEval):
if not isTree(tree): return modelEval(tree,inDat)
if inDat[tree['spInd']]>tree['spVal']:
if isTree(tree['left']):
return treeForeCast(tree['left'],inDat,modelEval)
else:
return treeForeCast(tree['right'],inDat,modelEval)
else:
if isTree(tree['right']):
return treeForeCast(tree['right'],inDat,modelEval)
else:
return treeForeCast(tree['left'],inDat,modelEval)
#批量数据预测
def createForeCast(tree,testData,modelEval = regTreeEval):
m = len(testData)
yHat = mat(zeros((m,1)))
for i in range(m):
yHat[i] = treeForeCast(tree,mat(testData[i]),modelEval)
return yHat
最终CART为:
# -*- coding: utf-8 -*-
'''
Created on Oct 12, 2010
Decision Tree Source Code for Machine Learning in Action Ch. 3
@author: Li
之前一个树节点存储一个属性就可以
现在一个节点需要存储,属性,切分点,左子树,右子树
'''
'''
可以这样面向对象编程,也可以不是
class treeNode():
def __init__(self,feature,value,left,right):
featureToSplit = feature
ValueToSplit = value
leftBranch = left
rightBranch = right
'''
from numpy import *
from sklearn import preprocessing
import operator
import treePlotter
#%% 读取回归数据和分类数据
'''
从文件中加载数据
'''
def loadDataSet(filename):
dataSet = []
fr = open(filename)
for line in fr.readlines():
curLine = line.strip().split('\t')
frtLine = list(map(float,curLine))#将每行映射成浮点数
dataSet.append(frtLine)
return dataSet
'''
分类数据加载,并将数据处理成用数字区分的,便于计算
'''
def loadClassData(filename):
dataSet = []
fr = open(filename)
for line in fr.readlines():
curLine = line.strip().split('\t')
dataSet.append(curLine)
dataSet = mat(dataSet)
m,n = shape(dataSet)
proData = zeros((m,n))
for feat in range(n):
temp = dataSet[:,feat]
temp = preprocessing.OneHotEncoder().fit_transform(array(temp).reshape(-1,1)).toarray()
temp = argmax(temp,axis = 1)
proData[:,feat] = temp
return proData
def binSplitDataSet(dataSet,feature,value):
def regLeaf(dataSet):
def regErr(dataSet,n):
def linearSolve(dataSet):
def modelLeaf(dataSet):
def modelErr(dataSet,n):
def majorityCnt(classList):
def classLeaf(dataSet):
def classErr(dataSet,n):
def chooseBestToSplit(dataSet,leafType = regLeaf,errType = regErr,ops = (1,4)):
def createTree(dataSet,leafType = regLeaf,errType = regErr,ops=(1,4)):
def isTree(obj):
def getMean(tree):
def prune(tree,testData):
def regTreeEval(model,inDat):
def modelTreeEval(model,inDat):
def classTreeEval(model,inDat):
def treeForeCast(tree,inDat,modelEval=regTreeEval):
def createForeCast(tree,testData,modelEval = regTreeEval):
def main():
filename = 'lenses.txt'
data = loadClassData(filename)
data = mat(data)
tree = createTree(data,classLeaf,classErr,ops=(0,0))
##tree = prune(tree,mat(loadDataSet('ex2test.txt')))
# pre = classify(tree,featureLabels,[0,0,0,1])
yHat = treeForeCast(tree,[0.,0.,0.,1.],modelEval=classTreeEval)
return tree,yHat
if __name__ == '__main__':
tree,yHat = main()
print(yHat)
几种算法的对比,对于连续纸,缺失值处理以及剪枝是一种处理思想,完全可以加在原始不支持的ID3算上,但是这就是数据预处理上的功夫了。其他两种方法则是在算法过程中进行处理。
| 算法 | 支持模型 | 树结构 | 特征选择 | 连续值处理 | 缺失值处理 | 剪枝 |
|---|---|---|---|---|---|---|
| ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 |
| C4.5 | 分类 | 多叉树 | 信息增益比 | 支持 | 支持 | 支持 |
| CART | 分类/回归 | 二叉树 | 基尼系数/均方差 | 支持 | 支持 | 支持 |
4 总结
摘自->
1)无论是ID3, C4.5还是CART,在做特征选择的时候都是选择最优的一个特征来做分类决策,但是大多数,分类决策不应该是由某一个特征决定的,而是应该由一组特征决定的。这样决策得到的决策树更加准确。这个决策树叫做多变量决策树(multi-variate decision tree)。在选择最优特征的时候,多变量决策树不是选择某一个最优特征,而是选择最优的一个特征线性组合来做决策。这个算法的代表是OC1。
2)如果样本发生一点点的改动,就会导致树结构的剧烈改变。这个可以通过集成学习里面的随机森林之类的方法解决。
优点
- 简单直观,生成的决策树很直观。
- 基本不需要预处理,不需要提前归一化,处理缺失值。
- 使用决策树预测的代价是O(log2m)。 m为样本数。
- 既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值
- 可以处理多维度输出的分类问题。
- 相比于神经网络之类的黑盒分类模型,决策树在逻辑上可以得到很好的解释
- 可以交叉验证的剪枝来选择模型,从而提高泛化能力。
- 对于异常点的容错能力好,健壮性高。
缺点:
- 决策树算法非常容易过拟合,导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。
- 决策树会因为样本发生一点点的改动,就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。
- 寻找最优的决策树是一个NP难的问题,我们一般是通过启发式方法,容易陷入局部最优。可以通过集成学习之类的方法来改善。
- 有些比较复杂的关系,决策树很难学习,比如异或。这个就没有办法了,一般这种关系可以换神经网络分类方法来解决。
- 如果某些特征的样本比例过大,生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。
5 习题
5.1 利用信息增益比生层决策树
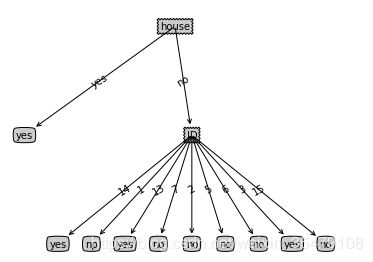
首先对比ID3算法,因为数据中为每个人分配了一个ID,他的信息增益是最大的,因此ID3算法倾向于将ID作为最优特征进行划分,结果如下:

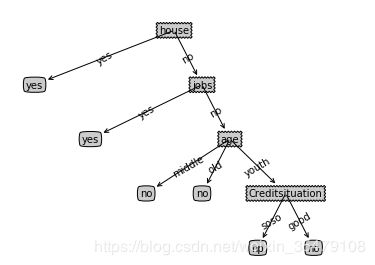
左图为ID3有ID列作为特征的时候生成的决策树,很明显会选择最优选择性的这一列作为区分,但是对一个新的样本进行预测只能靠瞎蒙了。右图去掉ID特征利用ID3生成树就差不多是正确的了,但是明显过拟合了,需要剪枝。
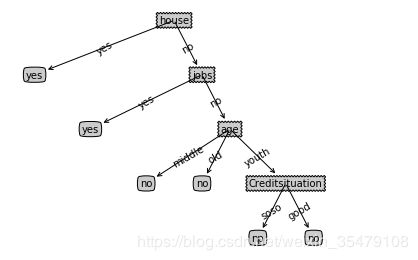
C4.5有ID时因为改变特征选择的方式,所以首先选择了house作为决策特征,效果好一些。右图的与ID3一样。
5.2 平方误差生成回归树
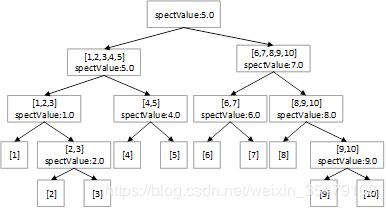
树结构:“”{‘left’: {‘left’: {‘left’: 4.5, ‘right’: {‘left’: 4.75, ‘right’: 4.91, ‘spInd’: 0, ‘spVal’: 2.0},‘spInd’: 0, ‘spVal’: 1.0}, ‘right’: {‘left’: 5.34, ‘right’: 5.8, ‘spInd’: 0, ‘spVal’: 4.0},‘spInd’: 0,‘spVal’: 3.0},
‘right’: {‘left’: {‘left’: 7.05, ‘right’: 7.9, ‘spInd’: 0, ‘spVal’: 6.0},‘right’: {‘left’: 8.23,‘right’: {‘left’: 8.7, ‘right’: 9.0, ‘spInd’: 0, ‘spVal’: 9.0},‘spInd’: 0,‘spVal’: 8.0},‘spInd’: 0,‘spVal’: 7.0},
‘spInd’: 0,‘spVal’: 5.0}
水平有限,将构成的树手动画出来……框中是根据最好的X值进行划分,到叶子节点的时候,满足spectVal的样本可能有很多,那么预测值取所有样本Y值的均值。这里生成的树对每一个样本都生成的了叶节点,显然过拟合了,但是对回归树的理解可能会加深一些。