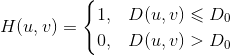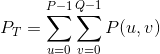图像处理之频率域滤波
频率域基础请参考“图像处理之频率域数学基础”。
通过傅里叶变换,可以把图像从空间域转换到频率域。图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。频率直接关系到图像空间灰度的变化率,低频对应于图像中变化缓慢的灰度,高频对应于图像中变化较快的灰度。一种解释是,频率对应的是傅里叶变换中的频率,频率越高,意味着正弦波变化得越快。
频率域滤波的基本过程是:修改一幅图像的傅里叶变换,然后计算其反变换得到处理后的结果。从而,得到基本滤波公式:
![]()
![]() 是傅里叶反变换,F(u,v)是输入图像f(x,y)的DFT,H(u,v)是滤波函数(或滤波器,或滤波传递函数),g(x,y)是滤波后的输出图像。函数F,H,g是与输入图像大小相同的M*N阵列。H(u,v)和F(u,v)是阵列相乘(元素对应位置相乘)。这里我们将F(u,v)中心化后再处理,即在变换前使用
是傅里叶反变换,F(u,v)是输入图像f(x,y)的DFT,H(u,v)是滤波函数(或滤波器,或滤波传递函数),g(x,y)是滤波后的输出图像。函数F,H,g是与输入图像大小相同的M*N阵列。H(u,v)和F(u,v)是阵列相乘(元素对应位置相乘)。这里我们将F(u,v)中心化后再处理,即在变换前使用![]() 乘输入图像来完成。
乘输入图像来完成。
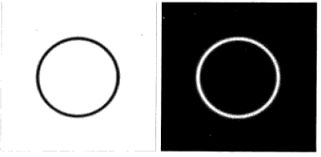
最简单的滤波器之一:变换的中心处是0,其他处是1。它抑制F(u,v)的直流项通过而通过其他所有项。因为直流项决定图像的平均灰度,将其置0将导致平均灰度为0,下图是一个例子(负灰度已置0):
为了得到滤波后的图像g(x,y),我们要确定滤波公式等号的右边部分。这里的方法是,在空间域对把图像f(x,y)0填充为P*Q大小,通过DFT得到F(u,v);然后,在频率域创建尺寸和填充过的图像一样的滤波器H(u,v)。
频率域滤波步骤:
- 给定一幅M*N的输入图像f(x,y),根据“图像处理之频率域数学基础”中的方法得到填充参数P和Q;
- 对f(x,y)0填充,得到大小为P*Q的图像
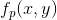 ;
; - 用
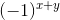 乘
乘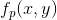 移到变换中心;
移到变换中心; - 计算第3步图像的DFT,得到F(u,v);
- 生成一个实的、对称的大小为P*Q的滤波函数H(u,v),中心在(P/2,Q/2)处,用阵列相乘得到:G(u,v) = H(u,v)F(u,v);
- 得到处理后的图像:
![g_{p}(x,y) = \{real[\mathfrak{F}^{-1}[G(u,v)]]\}(-1)^{x+y}](http://img.e-com-net.com/image/info8/9b99ff9c8a7f45288c269341cd109e96.gif) ,其中,real表示取实部,忽略因计算不准确导致的寄生复分量,下标p表示得到的是填充后的阵列;
,其中,real表示取实部,忽略因计算不准确导致的寄生复分量,下标p表示得到的是填充后的阵列; - 从
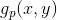 的左上象限提取M*N区域,得到最终处理结果g(x,y)。
的左上象限提取M*N区域,得到最终处理结果g(x,y)。
补充:
DFT是复数阵列,可以表示为实部和虚部之和:
![]()
则滤波公式变为:
![]()
发现这种滤波不能改变相位角。我们称等同地影响实部和虚部而不影响相位的滤波器为零相移滤波器。
空间域和频率域滤波的对应
考虑一维高斯滤波器:
![]()
空间域中的相应滤波器由H(u)的傅里叶反变换得到:
![]()
上面两个函数的表现是互易的:当H(u)有一个较窄的外形时(![]() 较小),h(x)有较宽的外形。频率域滤波器越窄,其衰减的高频越多,引起的模糊越大。在空间域,意味着必须用较大的模板来增加模糊。如下图:
较小),h(x)有较宽的外形。频率域滤波器越窄,其衰减的高频越多,引起的模糊越大。在空间域,意味着必须用较大的模板来增加模糊。如下图:
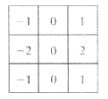
例:由空间模板得到频率域滤波器
上图是一个Sobel滤波器模板h(x,y),它是奇对称的,假如要处理的是一个600*600像素的图像f(x,y)。因为滤波器是3*3,所以我们将f和h填充为602*602像素。为保持Sobel模板的对称性,我们将它放到填充后的602*602图像的中心处得到,仍然保持奇对称,根据DFT的性质,可知H(u,v)将完全是虚函数。
产生H(u,v)的过程如下:
- 用
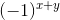 乘
乘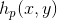 以便频率域滤波器“中心化”;
以便频率域滤波器“中心化”; - 计算1中结果的DFT;
- 因为H(u,v)是纯虚函数,将2中结果的寄生实部置0;
频率域滤波器平滑图像
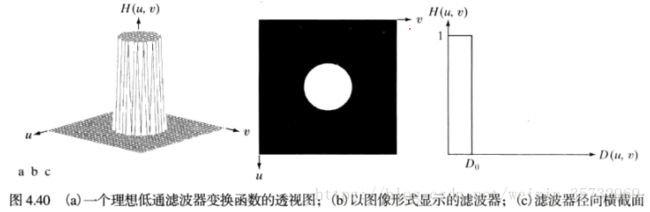
频率域平滑(模糊)可通过对高频的衰减来达到,也就是低通滤波。常用的3种类型低通滤波器:理想低通滤波器,布特沃斯低通滤波器和高斯低通滤波器。布特沃斯滤波器有一个“阶数”的参数,阶数较高时,接近理想滤波器,阶数较低时,接近高斯滤波器。
理想低通滤波器(ILPF):以原点为圆心,![]() 为半径的圆内,无衰减的通过所有频率,而在圆外切断所有频率的二维低通滤波器。由下面函数确定:
为半径的圆内,无衰减的通过所有频率,而在圆外切断所有频率的二维低通滤波器。由下面函数确定:
其中,![]() 是正常数,D(u,v)是频率域中点(u,v)与频率矩形中心的距离:
是正常数,D(u,v)是频率域中点(u,v)与频率矩形中心的距离:
![]()
其中,P和Q是填充后的尺寸。
截止频率:在H(u,v) = 1和H(u,v) = 0之间的过度点。下图中截止频率为![]() :
:
定义总图像功率值![]() :
:
其中,![]() 。如果DFT已被中心化,那么原点位于频率矩形中心处、半径为
。如果DFT已被中心化,那么原点位于频率矩形中心处、半径为![]() 的圆将包含
的圆将包含![]() 的功率,
的功率,![]() 为:
为:
总和取圆内或边界上的(u,v)值。
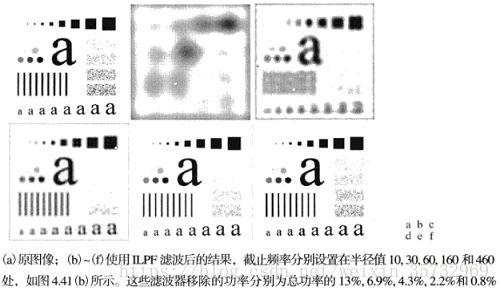
滤波效果如下:
上图中的结果都有振铃现象,可用卷积定理解释。因为ILPF在频率域的剖面图类似于盒状滤波器,可以预料相应的空间滤波器h(x,y)具有sinc函数形状,空间域滤波可通过h(x,y)与图像卷积实现。sin函数的中心波瓣是引起模糊的主因,而外侧较小的波瓣是造成振铃的主因。
截止频率位于距离原点![]() 处的n阶布特沃斯低通滤波器(BLPF):
处的n阶布特沃斯低通滤波器(BLPF):
与ILPF不同,BLPF并没有在通频率和滤除频率之间给出明显截止的尖锐的不连续性。对于具有平滑传递函数的滤波器,可以这样定义截止频率,即使得H(u,v)下降到其最大值的某个百分比的点。
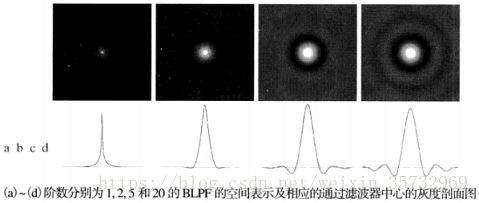
在空间域的一阶布特沃斯滤波器没有振铃现象;在二阶滤波器中,很难察觉振铃现象;更高阶的滤波器中振铃现象会很明显。下图解释了原因:
高斯低通滤波器(GLPF):
![]()
其中,![]() 是关于中心的扩展度的度量。令
是关于中心的扩展度的度量。令![]() ,则:
,则:
![]()
![]() 是截至频率。
是截至频率。
根据DFT的性质,GLPF的傅里叶反变换也是高斯的,这意味着得到的空间高斯滤波器将没有振铃(这是实际中一个重要特性,尤其在任何类型的人工缺陷不可接受的情况下,如医学影像)。
低通滤波器总结表:
频率域滤波器锐化图像
图像锐化可在频率域通过高通滤波实现,高通滤波会衰减低频分量而不会扰乱高频信息。
高通滤波器从给定的低通滤波器得到:
![]()
其中,![]() 是低通滤波器的传递函数。
是低通滤波器的传递函数。
根据前面提到的低通滤波器,高通滤波器可分为:理想高通滤波器(IHPF),布特沃斯高通滤波器(BHPF)和高斯高通滤波器(GHPF)。定义如下表:
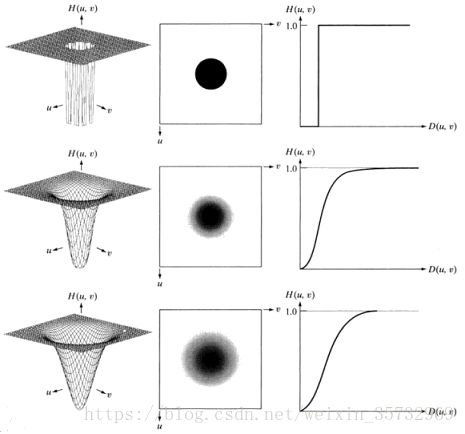
下图是高通滤波器的透视图,图像表示和剖面图,从上到下分别是IHPF,BHPF和GHPF:
选择性滤波
前面说的滤波器都是操作整个频率矩形,有时候需要操作某个小区域,如带阻滤波器和带通滤波器操作的是指定频段。
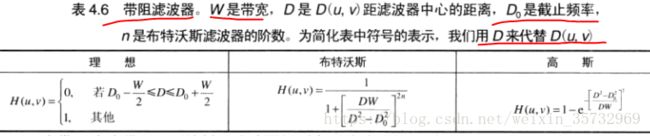
带阻滤波器总结如下:
带通滤波器从带阻滤波器得到:
![]()
下图左图为带阻高斯滤波器,有右图为相应的带通滤波器:
 微信交流
微信交流
 多谢打赏
多谢打赏
参考资料:冈萨雷斯《数字图像处理》
相关博文:图像处理之频率域数学基础