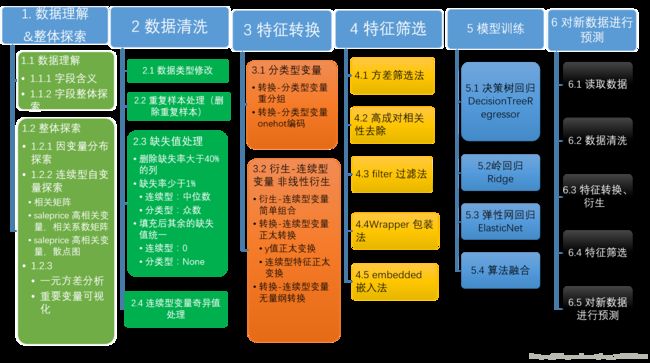
基于Kaggle的经典AI项目:预测房价系统
预测房价系统
Kaggle 项目链接:
http://www.kaggle.com/c/house-prices-adcvanced-regression-techniques/data
项目步骤:
完整代码
一、数据理解–整体探索
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib
from scipy.stats import norm
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.stats import skew
from scipy.stats.stats import pearsonr
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
#0 数据获取
#下载地址:https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data
train = pd.read_csv()
test = pd.read_csv()A 数据整体理解
train.info()B 数据探索
B1 因变量-房价
train['SalePrice'].describe() #概览 sns.distplot(train['SalePrice']).fit = norm #分布图B2 探索—数值型自变量
2.2.1 相关系数矩阵
DataFrame.corr() 给出两列之间的关系。利用该方法检测特征–目标变量之间的相关性corr = train.select_dtypes(include = [np.number]).iloc[:,1:].corr() plt.figure(figure = (12,12)) sns.heatmap(corr,vmax = 1,squre = True) #热力图显示所有变量之间的关系2.2.2 与saleprice 高相关变量,相关系数矩阵
corr_threshvalue = 0.5 #number of variables for heatmap corr_cols = corr.loc[:,corr.loc['SalePrice',:].abs() > corr_threshvalue].sort_value(by = 'SalePrice',axis = 1,ascending = False) corr_thresh = train[corr_cols].corr() plt.figure(figsize = (12,12)) sns.set(font_scales = 1.25) sns.heatmap(corr_thresh,cbar = True,annot = True,squre = True,fmt = '.2f',annot_kws = {'size': 10})2.2.3 与saleprice 高相关变量-散点图**
sns.pairplot(train[corr_cols],size = 2.5)B3 探索–分类型自变量
DataFrame.corr() 给出两列之间的关系。检测 特征–目标变量之间的相关性
train_cats = train.select_dtypes(include = [np.object]).iloc[:,1:] train_cats.head() train_cats.apply(lambda x:x.nunique())2.3.1 方差分析
一元方差分析(类型变量)def anova(train_cats_y,categorical,y): anv = pd.DataFrame(index = categorical) anv['feature'] = categorical pvals = [] for c in categorical: samples = [] for cls in train_cats_y[c].dropna().unique(): s = train_cats_y[train_cats_y[c] == cls][y].values samples.append(s) #某特征下不同取值对应的房价组合形成二维列表 pval = stats.f_oneway(*samples)[1] pvals.append(pval) anv['pval'] = pvals return anv.values['pval'] categorical = [column for column is train.column if train.dtypes[column] == 'object'] #类型变量集合 y = 'SalePrice' core_cate = anova(train,categorical,y) core_cate['disparity'] = np.log(20*1./core_cate['pval'].values)/np.log(20) #悬殊度悬殊度-绘图
fig.ax = plt.subplots(figure=(16,8)) sns.barplot(data = core_cate,x = 'feature',y = 'disparity') plt.xticks(rotation = 90) plt.show()
二、数据清洗
import pandas as pd
import numpy as np
import seaborn sns
import matplotlib
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.stats import skew
from scipy.stats.stats import pearsonr
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
import warnings
warnings.filterwarnings('ignore')
#数据读取
train = pd.read_csv('../07_数据/train.csv')
test = pd.read_csv('../07_数据/test.csv')
corr = train.corr()2.1 数据类型修改
train.dtypes将数据设置为对应的类型
train['MSSubClass'].dtypes #MSSubClass:出售房子类型,应该是分类型 train['YrSold'].dtypes #房子出售年月 train['MoSold'].dtypes train['MSSubClass'] = train['MSSubClass'].astype(str) #MSSubClass:出售房子类型,应该是分类型 train['YrSold'] = train['YrSold'].astypes(str) #房子出售年月 train['MoSold'] = train['MoSold'].astypes(str)2.2 重复样本处理
train.duplicated().sum() #查看重复样本个数 train.drop_duplicates(inplace = True) #删除重复样本2.3 缺失值处理
2.3.1 行–缺失值处理
(train.isnull().sum(axis=1)/train.shape[1] > 0.4).sum() #统计输出缺失值大于40%的行数 nans_del_index = train.index[(train.isnull().sum(axis=1)/train.shape[1] > 0.4)] train.drop(labels = nans_del_index,axis = 0,inplace=True)#删除缺失值大于40%的行数2.3.2 列–缺失值处理
类别型变量–区分度计算
def anova(train_cats_y,categorical,y): anv = pd.DataFrame(index = categorical) anv = ['feature'] = categorical pvals = [] for c in categorical: samples = [] for cls in train_cats_y[c].dropna().unique(): s = train_cats_y[train_cats_y[c] == cls][y].values samples.append(s) #某特征下不同取值对应的房价组合形成二维列表 pval = stats.f_oneway(*samples)[1] #一元方差分析得到F、P,要的是P,P越小对方差影响越大 pvals.append(pval) anv['pval'] = pvals return anv.values['pval'] categorical = [column for column is train.column if train.dtypes[column] == 'object'] #类型变量集合 y = 'SalePrice' core_cate = anova(train,categorical,y) core_cate['disparity'] = np.log(20*1./core_cate['pval'].values)/np.log(20) #悬殊度/区分度 #统计各列 缺失值比例 NAs = pd.concat([(100*train.isnull().sum(axis = 0)/train.shape[0]), 100*test.isnull().sum/train.shape[0]], axis = 1,keys = ['Train','Test']) NAs['type'] = train.dtypes[NAs.index] #加入类别型变量--相关度 NAs['corr_conti_y'] = train.corr()['SalePrice'] #加入类别型变量--区分度 NAs['core_cate_y'] = core_cate[disparity] #只保留有缺失值的列 NAs = NAs[NAs[['Train','Test']].sum(axis=1) > 0].sort_values(by = 'True',ascending = False)#删除缺失值大于40%的列 nans_del_cols = NAs.index[((NAs[['Train','Test']] > 40).sum(axis=1) > 0).values] nans_del_cols train.drop(labels = nans_del_cols,axis=1,inplace = True) #统一填充缺失率少于1% 的列(连续型--中位数;分类型--众数) nans_del_cols = NAs.index[((NAs[['Train','Test']] < 1).sum(axis=1)==2).values].values nans_del_cols nans_del_cols_num = train[nans_lessl_cols].select_dtypes(include=[np.number]).column nans_del_cols_class = train[nans_lessl_cols].select_dtypes(include=[np.object]).column train[nans_del_cols_num] = train[nans_del_cols_num].fillna(train[nans_del_cols_num].median()) train[nans_del_cols_class] = train[nans_del_cols_class].fillna(train[nans_del_cols_class].mode()) #相关性高的连续型变量业务填充 #GarageTrBlt: 车库建成日期,用房屋建成日期替代 #KasVarArea: 外墙装饰面积 #LotFrontage: 房子与街道距离 train.loc[train['GarageTrBlt'].isnull(),'GarageTrBlt'] = train.loc[train['GarageTrBlt'].isnull(),'YearBuilt'] train['KasVarArea'] = train['KasVarArea'].fillna(0) train['LotFrontage'] = train['LotFrontage'].fillna(0) #区分度高的 分类型变量业务填充 #BsmtQual: 地下室质量 #KitchenQual: 厨房质量 train['BsmtQual'].fillna('None',inplace=True) train['KitchenQual'].fillna(train['KitchenQual'].mode(),inplace=True) #统一填充剩余变量(连续型--0;分类型--None) #查看剩余变量情况 remain_col = train.columns[train.isnull().sum(axis=0) > 0] NAs.loc[remain_col,] nans_remain_cols_num = train[remain_col].select_dtypes(include=[np.number]).column nans_remain_cols_class = train[remain_col].select_dtypes(include=[np.object]).column train[nans_remain_cols_num] = train[nans_remain_cols_num].fillna(0) train[nans_remain_cols_class] = train[nans_remain_cols_class].fillna(None) #查看缺失值是否出完毕 train.isnull().sum(axis=0)2.4 连续型变量奇异值处理
train.SalePrice.plot(king = 'box',sym = 'b+') #y 变量箱线图 number_para = train.select_dtypes(include = [np.number]).drop('id',axis=1) #查看与y变量高相关性变量的箱线图 corr = number_para.corr() corr_threshvalue = 0.5 #number of variables for heatmap corr_cols = corr.loc[:,corr.loc['SalePrice',:].abs() > corr_threshvalue].columns number_para[corr_cols].plot(sym='b+',king = 'box',subplots=True,figsize=(20,8)) #找到奇异值上下的临界点 number_para_q = number_para.quantile(q =[0,0.05,0.25,0.5,0.75,0.95,1],axis = 0) number_para_q #outlier_expand为异常值定义伸缩参数,标准为 1.5 outlier_expand = 2 number_para_q.loc['lower_outlier',:] = number_para_q.loc[0.25,:]- (number_para_q.loc[0.75,:]- number_para_q.loc[0.25,:])*outlier number_para_q.loc['upper_outlier',:] = number_para_q.loc[0.75,:]+ (number_para_q.loc[0.75,:]- number_para_q.loc[0.25,:])*outlier #统计各个列中高于/低于 上下临界点的数量 upper_cnt = (number_para > number_para_q.loc['upper_outlier',:]).sum() upper_cnt lower_cnt = (number_para < number_para_q.loc['lower_outlier',:]).sum() lower_cnt2.4.1 重点变量处理
#bivariate analysis salarprice/grlivares var = 'GrLivAreas' data = pd.concat(train['SalePrice'],train[var],axis=1) data.plot.scatter(x = var,y = 'SalePrice',ylim = (0.800000)); #dalecting points train.sort_values(by = 'GrLivAreas',ascending = False)[:2] train = train.drop(train[train['Id'] == 1299].index) train = train.drop(train[train['Id'] == 524].index)2.4.2 其余变量统一处理
number_para = number_para.where(number_para < number_para_q.loc['upper_outlier',:], number_para_q.loc['upper_outlier',:],axis=1) number_para = number_para.where(number_para < number_para_q.loc['lower_outlier',:],number_para_q.loc['lower_outlier',:],axis=1) number_para[corr_cols].plot(sym = 'b+',kind = 'box',subplots = True,figure = (20,8))
三、特征转换
import pandas as pd
import numpy as np
import seaborn sns
import matplotlib
import scipy.stats import norm
from scipy import stats
import matplotlib.pyplot as plt
#matplotlib inline
from scipy.stats import skew
from scipy.stats.stats import pearsonr
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'准备工作–引入‘数据清洗’处理
%run '数据清洗.ipynb'类别型变量–区分度计算
def anova(train_cats_y,categorical,y): anv = pd.DataFrame(index = categorical) anv = ['feature'] = categorical pvals = [] for c in categorical: samples = [] for cls in train_cats_y[c].dropna().unique(): s = train_cats_y[train_cats_y[c] == cls][y].values samples.append(s) #某特征下不同取值对应的房价组合形成二维列表 pval = stats.f_oneway(*samples)[1] #一元方差分析得到F、P,要的是P,P越小对方差影响越大 pvals.append(pval) anv['pval'] = pvals anv['disparity'] = np.log(20*1./core_cate['pval'].values)/np.log(20) #悬殊度/区分度 return anv.sort_values['pval'] categorical = [column for column is train.column if train.dtypes[column] == 'object'] #类型变量集合 y = 'SalePrice' core_cate = anova(train,categorical,y) cate_feature #统计变量的主要信息 train_ana = pd.DataFrame() train_ana['feature_type'] = train.dtypes #加入变量类型 train_ana['cate_cnt'] = train,apply(lambda x : x.nuique()) #加入每个类别型变量的取值个数 train_ana['conti_corr'] = train.corr()['SalePrice'] #加入连续型变量相关度 train_ana['cate_coor'] = train.corr()['disparity'] #加入类别型变量--区分度 #train_ana.sort_values(by = ['feature_type','cate_cnt','conti_corr','cate_coor'],ascending = False3.1 分类型变量
train_ana.loc[train_ana.feature_type == 'object',].sort_values('cate_cnt',ascending = False)3.1.1 转换-分类型变量–重分组
neighborhood_order = train.groupby('Neighborhood').median().sort_values(by = 'SalePrice').index plt.figure(figsize = (24,6)) sns.boxplot(x = 'Neighborhood',y = 'SalePrice',data = train,order = neighborhood_order) plt.xticks(rotation = 45) #画布旋转45度 plt.figure(figsize = (24,6)) sns.boxplot(x = 'Neighborhood',data = train,order = neighborhood_order) plt.xticks(rotation = 45) neighborhood_order train['SimpleNeighborhood'] = train.Neighborhood.replace({'IDOTRR':'IDOTRR-BrDale','BrDale':'IDOTRR-BrDale', 'Blueste':'Blueste-SWISU','SWISU':'Blueste-SWISU', 'NPkVill':'NPkVill-Mitchel','Mitchel':'NPkVill-Mitchel' }) anova(train,['Neighborhood','SimpleNeighborhood'],y)3.1.2 转换-分类型变量–onehot编码
#通过onehot编码创建虚拟特性分类值 train_cat = train.select_dtypes(include = [np.object]) train_onehot = pd.get_dummies(train_cat)3.2 连续型变量
train_ana.loc[train_ana.feature_type != 'object',].sort_values('conti_corr',ascending = False)3.2.1 衍生-连续型变量—非线性衍生(平/立方后再求平方根)
train['OverallQual-s2'] = train['OverallQual']**2 train['OverallQual-s3'] = train['OverallQual']**3 train['OverallQual-Sq'] = np.sqrt(train['OverallQual']) train['GrLivAreas-2'] = train['GrLivAreas']**2 train['GrLivAreas-3'] = train['GrLivAreas']**3 train['GrLivAreas-Sq'] = np.sqrt(train['GrLivAreas']) train[('SalePrice','OverallQual','OverallQual-s2','OverallQual-s3','OverallQual-Sq', 'GrLivAreas','GrLivAreas-2','GrLivAreas-3','GrLivAreas-Sq')].coor()['SalePrice']3.2.2 衍生-连续型变量—简单组合(自变量相加)
train['TotalBath'] = train['BsmtFullBath'] + (0.5*train['BsmtFullBath']) + \ train['FullBath'] + (0.5*train['halfBath']) #Total of bathrooms train['AllSF'] = train['GrLivAreas'] + train['TotalBsmtSF'] #Total SF for house(incl,basement) train['AllFlrsSF'] = train['1stFlrSF'] + train['2ndFlrSF'] #1st + 2nd floor train['AllPorchSF'] = train['OpenPorchSF'] + train['EnclosedPorch'] + \ train['3SsnPorchSF'] + train['ScreenPorch'] train[['TotalBath','AllSF','AllFlrsSF','AllPorchSF']].corr()['SalePrice']3.2.3 转换-连续型变量-正太转换
y 值正太变换
sns.distplot(train['SalePrice'],fit = norm) #分布图 stats.probplot(train['SalePrice'],plot = plt) #利用Q-Q图判断数据是否偏离正太分布 train['SalePrice_log'] = np.loglp(train['SalePrice']) #取对数-分布图 stats.probplot(train['SalePrice'],plot = plt) #利用Q-Q图判断数据是否偏离正太分布 train.corr().sort_values('SalePrice_log',ascending = False)[['SalePrice','SalePrice_log']]连续型特征-正态分布
#对数值特征进行变换,来减少倾斜异常值的影响 #一般的经验法则,绝对偏态值 > 0.75 被认为是倾斜严重train_num = train.select_dtypes(include = [np.number]).drop(['SalePrice'],['SalePrice_log'],axis = 1) skewness = train_num.apply(lambda x : skew(x.dropna())) skewness = skewness[abs(skewness) > 0.75] skewness skew_features = skewness.index train[skew_features] = np.loglp(train[skew_features])3.2.4 转换-连续型变量 无量纲转换
from sklearn.preprocession import MinMaxScaler train_num = train.select_dtypes(include = [np.number]).drop(['SalePrice'],['SalePrice_log'],axis = 1) min_max_scaler = MinMaxScaler() X_trian_minmax = min_max_scaler.fit_transform(train_num) train_num_minmax = np.round(min_max_scaler.transform(train_num),2) train_num_minmax = pd.DataFrame(train_num_minmax,columns = train_num.columns + '_minmax',index = train.index) train = pd.concat([train,train_onehot,train_num_minmax],axis = 1) train.drop(['SalePrice_log'],axis = 1,inplace = 'True')
四、特征筛选
#Embedded 嵌入法
import pandas as pd
import numpy as np
import seaborn sns
import matplotlib
import scipy.stats import norm
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.stats import skew
from scipy.stats.stats import pearsonr
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
%run'特征转换、衍生.ipynb'
train_num = train.select_dtypes(include = [np.number]).drop(labels = ['Id','SalePrice'],axis = 1)
train_num.shape4.1 方差筛选法
去除低方差没有波动的变量
from sklearn.feature_selection import VarianceThreshold varthreshold = 0.01 #设置阈值 sel_varthres = VarianceThreshold(threshold = varthreshold) sel_varthres.fit(train_num) sel_not_varthrea_var = train_num.columns[np.logical_not(sel_varthres.get_support())] sel_varthres_var = train_num,columns[(sel_varthres.get_support())] sel_not_varthrea_var plt.hist(train_num['Street']) train_num = train_num[sel_varthres_var] train_num.shape4.2 Filter 过滤法
相关系数法 pearsonr ,或直接用corr 阈值法
from sklearn.feature_selection import SelectPercentile from scipy.stats import pearsonr import numpy as np sel_percentbest = SelectPercentile(lambda X,Y: np.array(map(lambda x: pearsonr(x,y)[0],X.T)).T,percent = 80) sel_percentbest.fit(train_num,train['SalePrice']) sel_percentbest_var = train_num.columns[sel_percentbest.get_support()] sel_percentbest_var train_num = train_num[sel_percentbest_var] train_num.shape4.3 Wrapper 包装法
from sklearn.feature_selection import RFE #特征选择算法 from sklearn.ensemble import RandomForestRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.tree import DecisionTreeClassifier rf = RandomForestRegressor(n_estimators = 400) sel_rfe = RFE(rf.n_feature_to_select = int(train_num.shape[1]*0.8)) sel_rfe = fit.(train_num,train['SalePrice_log']) sel_rfe_var = train_num.columns[sel_rfe.get_support()] sel_rfe_var train_num = train_num[rfe_var] train_num.shape4.4 Embedded 嵌入法
from sklearn.feature_selection import SelectFromModel from sklearn.ensemble import RandomForestRegressor rf = =RandomForestRegressor(n_estimators = 400) sel_frommodel = SelectFromModel(rf,threashold = '0.5*median') sel_frommodel = fit.(train_num,train['SalePrice_log']) sel_frommodel_var = train_num.columns[sel_frommodel.get_support()] sel_frommodel_var train_num = train_num[sel_frommodel_var] train_num.shape
五、模型训练
---------------------集成算法----------------------- #引入‘特征筛选’处理 %run '特征筛选.ipynb' train_y = train_num['SalePrice_log'] train_x = train_num.drop('SalePrice_log',axis = 1) model_column = train_x.columns train_x.shape model_column----------------决策回归树算法--------------------------- from sklearn.tree import DecisionTreeRegressor from sklearn.sqrt_search import GridSearchCV # 参数优化--交叉检验 tuned_parameters = { 'criterion':['mse'], 'min_samples_split':[2,10,20], 'max_depth':[2,10,20,40], 'min_samples_leaf':[1,5,10], 'max_leaf_nodes':[2,10,20,40], } clf = DecisionTreeRegressor() clf = GridSearchCV(dlf,tuned_parameters,cv=5) clf.fit(train_x,train_y) clf.best_params_ for params,mean_score,scores in clf.grid_score_: print('$0.3f(+/-%0.03f) for %r' %(mean_score,scores.std()*2,params)) #可视化----模型结果展示----变量重要性显示 important_features = pd.Series(data = clf.best_estimator_.feature_importances_,index = train_X.columns).sort_values(ascending = False) plt.figure(figsize = (20,10)) important_features.plot(king = 'bar') #效果评估 from sklearn.metrics import mean_squared_error pred_y = clf.predict(train_X) np.sqrt(mean_squared_error(np.expml(train_y),np.expml(pred_y))) plt.figure(figsize = (20,10)) plt.scatter(x = np.expml(train_y),y = np.expml(pred_y))********岭回归 Ridge************ from sklearn.linear_model import Ridge from sklearn.model_selection import cross_val_score from sklearn.model_selection import KFold # 参数优化--交叉检验 n_folds = 5 def rmse_cv(model): rmse = np.sqrt(-cross_val_score(model,train_X,train_y,scoring = 'neg_mean_squared_error',cv = KFold(n_folds,shuff))) return(rmse) alphas = [0.05,0.1,0.3,1,3,5] cv_ridge = [rmse_cv(Ridge(alpha = alpha)).mean() for alpha is alphas] #score.std() cv_ridge = pd.Series(cv_ridge,index = alphas) cv_ridge.plot(title = 'Validation - LassoCV') plt.xlabel('alpha') plt.ylabel('rmse') ridge = Ridge(alpha = 1) ridge.fit(train_X,train_y) #可视化----模型结果展示----变量重要性显示 important_features = pd.Series(data = ridge.coef_,index = train_X.columns).sort_values(ascending = False) important_features = important_features[np.abs(important_features) > 0.01] plt.figure(figsize = (20,10)) important_features.plot(king = 'bar') #效果评估 from sklearn.metrics import mean_squared_error pred_y = ridge.predict(train_X) np.sqrt(mean_squared_error(np.expml(train_y),np.expml(pred_y))) plt.figure(figsize = (20,10)) plt.scatter(x = np.expml(train_y),y = np.expml(pred_y))3 ********弹性网回归 ElasticNet ************ from sklearn.linear_model import ElasticNetCV # 参数优化--交叉检验 elasticNet = ElasticNetCV(1l_ratio = [0.1,0.3,0.5,0.6,0.7,0.8,0.85,0.9,0.95,1], alpha = [0.0001,0.0003,0.0006,0.001,0.003,0.006, 0.01,0.03,0.06,0.1,0.3,0.6,1,3,6], max_iter = 50000,cv = 10) elasticNet.fit(train_X,train_y) alpha = elasticNet.alpha_ ratio = elasticNet.1l_ratio_ print('Best 1l_ratio:',ratio) print('Best alpha:',alpha) print('Try again for more precision with 1l_ratio centered around' + str(ratio)) elasticNet = ElasticNetCV(1l_ratio = [ratio + .85,ratio + .9,ratio + .95,ratio + .9,ratio,ratio + 1.05,ratio + 1.1,ratio + 1] alphas = [0.0001,0.0003,0.0006,0.001,0.003,0.006,0.01,0.03,0.06,0.1,0.3,0.6,1,3] max_iter = 50000,cv = 10) elasticNet.fit(train_X,train_y) if(elasticNet.1l_ratio_ > 1): elasticNet.1l_ratio_ = 1 alpha = elasticNet.alpha_ ratio = elasticNet.1l_ratio_ print('Best 1l_ratio:',ratio) print('Best alpha:',alpha) print('Now try again for more precision on alpha,with 1l_ratio fixed at' + str(ratio)+'and alpha centered around' + str(alpha)) elasticNet = ElasticNetCV(1l_ratio = ratio, alphas = [alpha + .6,alpha + .65,alpha + .7,alpha + .75,alpha + .8, alpha + .85,alpha + .6,alpha + .95,alpha,alpha + 1.05,alpha + 1.1, alpha + 1.15,alpha + 1.25,alpha + 1.25,alpha + 1.35,alpha + 1.4], max_iter = 50000,cv = 10) elasticNet.fit(train_X,train_y) if(elasticNet.1l_ratio_ > 1): elasticNet.1l_ratio_ = 1 alpha = elasticNet.alpha_ ratio = elasticNet.1l_ratio_ print('Best 1l_ratio:',ratio) print('Best alpha:',alpha) #模型稳定性 score = rase_cv(elasticNet) print('Averaged base models score:{: .4f}({: .4f})\n'.format(score.mean(),score.std())) #Averaged base model score:0.1199(0.0098) #可视化----模型结果展示----变量重要性显示 important_features = pd.Series(data = elasticNet.coef_,index = train_X.columns).sort_values(ascending = False) important_features = important_features[np.abs(important_features) > 0.01] plt.figure(figsize = (20,10)) important_features.plot(king = 'bar') #效果评估 from sklearn.metrics import mean_squared_error pred_y = elasticNet.predict(train_X) np.sqrt(mean_squared_error(np.expml(train_y),np.expml(pred_y))) plt.scatter(pred_y,pred_y - train_y, c = 'blue',marker = 's',label = 'Training data') plt.hlines(y = 0,xmin = 10.5,xmax = 13.5,color = 'red') #Plot predictions plt.scatter(pred_y,train_y, c = 'blue',marker = 's',label = 'Training data') plt.plot([10.5,13.5],[10.5,13.5], c = 'red')#4***********算法融合************* from sklearn.base import BaseEstimator from sklearn.base import RegressorMixin from sklearn.base import TransformerMinin from sklearn.base import clone class AveragedModel(BaseEstimator,RegressorMixin,TransformerMinin): def __init__(self,models): self.models = models # we define clones of the original models to fit the data in def fit (self,x,y): self.model_ = [clone(x) for x in self.models] #Train cloned base models for model in self.models_: model.fit(X,y) return self #Now we do the predictions for cloned model and average them def predict(self,X): predictions = np.column_stack([ model.predict(X) for model in self.models_ ]) return np.mean(predictions,axis = 1) #模型相关性分析 pred_y_ridge = ridge.predict(train_X) pred_y_elasticNet = elasticNet.predict(train_X) pred_y_clf = clf.predict(train_X) from scipy.stats import pearsonr pearsonr(pred_y_ridge.T,pred_y_elasticNet.T) pearsonr(pred_y_clf.T,pred_y_elasticNet.T) #模型训练 average_models = AveragedModels(models = (ridge,elasticNet)) average_models.fit(train_X,train_y) #交叉验证 n_folds = 5 def rmse_cv(model): rmse = np.sqrt(-cross_val_score(model,train_X,train_y,scoring = 'neg_mean_squared_error', cv = KFold(n_folds,shuffle = True,random_stats = 42))) return(rmse) score = rmse_cv(average_models) print('Averaged base models score:{: .4f}({: .4f})\n'.format(score.mean(),score.std())) #效果评估 from sklearn.metrics import mean_squared_error pred_y = average_models.predict(train_X) np.sqrt(mean_squared_error(np.expml(train_y),np.expml(pred_y))) plt.scatter(pred_y,pred_y - train_y, c = 'blue',marker = 's',label = 'Training data') plt.hlines(y = 0,xmin = 10.5,xmax = 13.5,color = 'red') #Plot predictions plt.scatter(pred_y,train_y, c = 'blue',marker = 's',label = 'Training data') plt.plot([10.5,13.5],[10.5,13.5], c = 'red')5*************最终模型************** model_ridge = ridge model_elasticNet = elasticNet model_averaged_model = averaged_models import pandas as pd import numpy as np import seaborn sns import matplotlib from scipy import stats import matplotlib.pyplot as plt %matplotlib inline from scipy.stats import skew from scipy.stats.stats import pearsonr from IPython.core.interactiveshell import InteractiveShell InteractiveShell.ast_node_interactivity = 'all' import warnings warnings.filterwarnings('ignore') #1 读取数据 test = pd.read_csv('../07_数据/test.csv') test.shape #2 数据清洗 #run'2-数据清洗.ipynb' test['MSSubClass'] = test['MMubClass'].astypes(str) #年月 test['TearBuilt'] = test['YearBuilt'].astypes(str) test['YrSold'] = test['YrSold'].astypes(str) test['MoSold'] = test['MoSold'].astypes(str) #重复值处理--删除重复值 test.drop_duplicates(inplace = True) #3.2.1 删除缺失值大于40%的列 test.drop(labels = clear_nans_del_cols,axis = 1,inplace = True) #3.2.3 相关性高的连续型变量业务填充 test.loc[test['GarageTrBlt'].isnull(),'GarageTrBlt'] = test.loc[test['GarageTrBlt'].isnull(),'YearBuilt'] test['KasVarArea'] = test['KasVarArea'].fillna(0) test['LotFrontage'] = test['LotFrontage'].fillna(0) #3.2.4 区分度高的分类型变量业务填充 test['BsmtQual'].fillna('None',inplace = True) test['KitchenQual'].fillna(clear_KitchenQual_mode,inplace = True) #3.2.5 统一填充剩余变量(连续型--0;分类型--None) remain_col = test.columns[test.isnull().sum(axis = 0) > 0] clear_nans_remain_cols_sum = test[remain_col].select_dtypes(include = [np.number]).columns clear_nans_remain_cols_class = test[remain_col].select_dtypes(include = [np.object]).columns test[clear_nans_remain_cols_sum] = test[clear_nans_remain_cols_sum].fillna(0) test[clear_nans_remain_cols_class] = test[clear_nans_remain_cols_class].fillna('None') #查看缺失值是否出完毕 test.isnull().sum(axis = 0).sum()****************对新数据进行预测**************** %run'5-模型训练。ipynb' test_X = test_num[model_column] test_ID = test['Id'] pred_y_ridge = np.expml(model_ridge.predict(test_X)) pred_y_elasticNet = np.expml(model_elasticNet.predict(test_X)) pred_y_averaged_models = np.expml(pred_y_averaged_models.predict(test_X)) sub1 = pd.DataFrame() sub1['Id'] = test_ID sub1['SalePrice'] = pred_y_ridge sub1.to_csv('sub_ridge.csv',index = False) sub2 = pd.DataFrame() sub2['Id'] = test_ID sub2['SalePrice'] = pred_y_elasticNet sub2.to_csv('sub_elasticNet.csv',index = False) sub3 = pd.DataFrame() sub3['Id'] = test_ID sub3['SalePrice'] = pred_y_averaged_models sub3.to_csv('sub_averaged_models.csv',index = False)