卡尔曼滤波在温度测量上的应用

简介

对于卡尔曼滤波，我相信很多机器人相关专业的同学都不陌生，网上搜索下关键词相关的资料也很多，但是大部分都是给你介绍相关的公式推导，对于数学基础好点的同学来说看了遍之后会觉得好像是那么回事，但是回头一想会觉得这东西怎么用啊，如何把它的效果在实际工程应用中发挥出来啊，如果做不到这一点那么对于你来说卡尔曼滤波还是遥不可及的梦。其实我觉得卡尔曼滤波这个名字是具有迷惑性的，以至于我们会把他归类于低通滤波，高通滤波这类的滤波器当中，在学习了相关理论后你会发现卡尔曼滤波并不是一般的滤波器而是一种“”“预测”，根据当前时刻的测量值和上一时刻的估计值预测当前时刻的最优值，所以这里我们就可以看出来卡尔曼滤波不是简单地滤除某些高频或者低频噪声而是对真实值的预测。

卡尔曼滤波算法

1960年，Kalman首次提出卡尔曼滤波，卡尔曼滤波刚一提出人们就发现了其在军事上的巨大应用前景，阿波罗登月、飞机导弹的导航系统成功应用就是最好的例证。，卡尔曼滤波器是时域内直接设计的最优滤波器，1961 年卡尔曼有将这一滤波理论推广到连续时间系统中，也就形成了卡尔曼滤波的完整体系，对于系统噪声是高斯分布的线性系统可以递推出最小均方差估计。
从本质上来讲卡尔曼滤波其实就是反馈控制，其实现的思路如下图所示。滤波器估计过程中某一个时刻的状态，利用量测更新的值作为反馈。所以卡尔曼滤波过程又可以分为状态跟新和测量更新两个部分来实现。状更新中主要是为了获得下个时刻的先验估计，量测更新则是为了通过先验估计和量测值获取后验估计。这就是卡尔曼思想中采用的迭代方式。具体的过程如下
状态一步预测：
${\hat{x}}_{k|k-1}={\Phi }_{k|k-1}{\hat{x}}_{k-1}$
状态估计：
${\hat{x}}_k={\hat{x}}_{k|k-1}+K_k\left(z_k-H_k{\hat{x}}_{k|k-1}\right)$
计算滤波增益：
$K_k=P_{k,k-1}{H}_k^T{\left(H_k{P}_{k|k-1}{H}_k^T+R_k\right)}^{-1}$
一步预测方差矩阵：
$P_{k|k-1}={\Phi }_{k|k-1}{P}_{k-1}{\Phi }_{k|k-1}+{\Gamma }_{k|k-1}{Q}_{k-1}{\Gamma }_{k|k-1}^T$
估计误差方差阵：
$P_k=\left(I-K_k{H}_k\right)P_{k|k-1}\left(I-K_k{H}_k\right)+K_k{R}_k{K}_k^T$

具体的推导过程就不表了，相信大家在网上都能找到，从这五条公式中我们可以看到一下几个要点，第一个就是初始状态的选取，第二个就是噪声矩阵大小的选取。对于第一个问题需要根据实际情况来判断，比如说对于加速速计，一般来说它的初始值是Z轴方向为重力加速度值g，其他两个轴为0，而对于温度传感器，由于在不同环境下它的初始值都不一样所以我们可以选择第一个测量值作为初始值，但是无论怎么选择其实是不会影响最终的结果的只会影响到收敛速度。而对于第二个问题我之前也是查阅了大量的资料，发现很多人其实没有直面这个问题，一种比较靠谱的方法是将实时运行的数据保存下来导入到matlab中，然后在matlab中调试出比较好的Q，R参数。下面举一个例子

卡尔曼滤波算法对温度的估计

对温度系统的估计是卡尔曼应用中最常使用的案例，我们首先采集一段温度传感器读取的室内温度，然后在matlab中进行计算，matlab代码如下

N=1000; 
size=[N,1]; 

%取温度预测值的方差为Q=1e-2,温度传感器的测量方差为R=0.36，即我们更相信预测值，而较少相信传感器测量值。
Q=0.001;  
R=0.36;
a=0.1;
% T_mearsured=T+sqrt(R)*randn(size);
T_mearsured=load('temperature_data.txt');
%初始时刻温度的最优估计值为T_start=22.5度,温度初始估计方差为P_start=2
lowpass_filter(1)=T_mearsured(1);
T_start=T_mearsured(1);  P_start=2;
T_kalman(1)=T_start;  P_kalman(1)=P_start;
%用_kalman的后缀表示最优估计值，用_pre的后缀表示预测值
for k=2:N
%在进行温度预测时，因为温度是一个连续的状态，我们认为上一时刻的温度和当前时刻的温度相等，则有T(k)=T(k-1)。
T_pre(k)=T_kalman(k-1);
P_pre(k)=P_kalman(k-1)+Q;
K(k)=P_pre(k)/(P_pre(k)+R);
T_kalman(k)=T_pre(k)+K(k)*(T_mearsured(k)-T_pre(k));
P_kalman(k)=P_pre(k)-K(k)*P_pre(k);
end
%画图
figure();
plot(T_mearsured,'-k');
hold on
plot(T_kalman,'r');
legend('温度测量值','Kalman估计值')

运行结果如下

黑色是我们实际测量的数据，红色是经过卡尔曼滤波算法后的数值，可以看到滤波后的效果还是很明显的，这里可以看到我设置的Q、R值分别是0.01和0.36我们改一下这个值看看会有啥不同，当我们把Q的值改为0.5时可以看到效果为

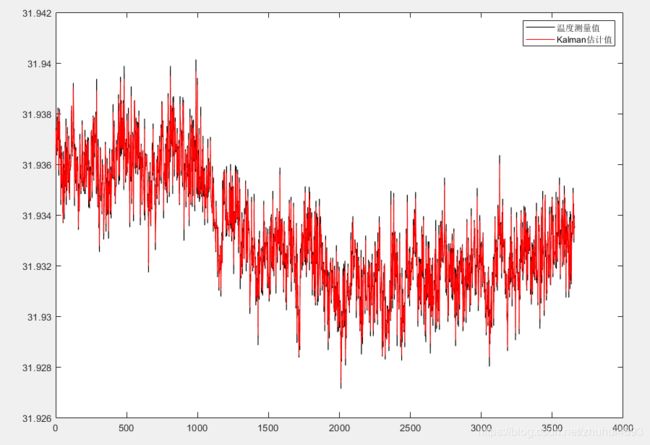
两条线的重合度更高，这也是符合理论的，因为增大了系统噪声，说明我们更信赖测量值，与测量值关系就更密切。
对应的C语言代码为

*-------------------------------------------------------------------------------------------------------------*/
/*       
        Q:过程噪声，Q增大，动态响应变快，收敛稳定性变坏
        R:测量噪声，R增大，动态响应变慢，收敛稳定性变好       
*/

#define KALMAN_Q 0.02

#define KALMAN_R 7.0000

/* 卡尔曼滤波处理 */

static double KalmanFilter(const double ResrcData,double ProcessNiose_Q,double MeasureNoise_R)
{

    double R = MeasureNoise_R;
    double Q = ProcessNiose_Q;

    static double x_last;
    double x_mid = x_last;
    double x_now;

    static double p_last;
    double p_mid ;
    double p_now;

    double kg;

    x_mid=x_last;                       //x_last=x(k-1|k-1),x_mid=x(k|k-1)
    p_mid=p_last+Q;                     //p_mid=p(k|k-1),p_last=p(k-1|k-1),Q=噪声

    /*
     *  卡尔曼滤波的五个重要公式
     */
    kg=p_mid/(p_mid+R);                 //kg为kalman filter，R 为噪声
    x_now=x_mid+kg*(ResrcData-x_mid);   //估计出的最优值
    p_now=(1-kg)*p_mid;                 //最优值对应的covariance
    p_last = p_now;                     //更新covariance 值
    x_last = x_now;                     //更新系统状态值

    return x_now;

}

我们将经过滤波的数据和没有滤波的通过单片机的串口发送出来将数据导入到matlab中，可以看到效果如下

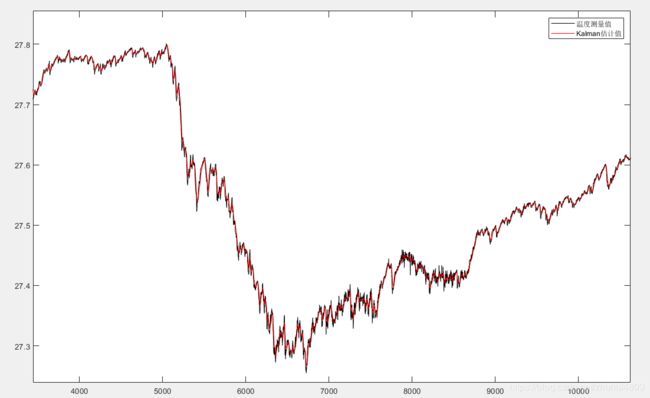
可以看到实际的工程应用效果也是比较明显的，符合我们的预期。