主席树/函数式线段树/可持久化线段树

【前言】

主席树、函数式线段树、可持久化线段树
这三者其实是一个东西……
它的作用十分显然，就是访问线段树的历史版本……

【实现】

假设我们要对线段树进行Q次插入操作，如何（随机）访问第i次操作后的线段树？

我们当然可以对每个状态都造一棵完整的线段树，但是显然会MLE啊，怎么办？
观察可以发现，线段树的插入操作每次只会更新logN个节点，其他节点都不会变
于是我们可以利用前一次操作的状态，避免重复构造不变节点。
如何实现对不变节点的利用呢？看下图：

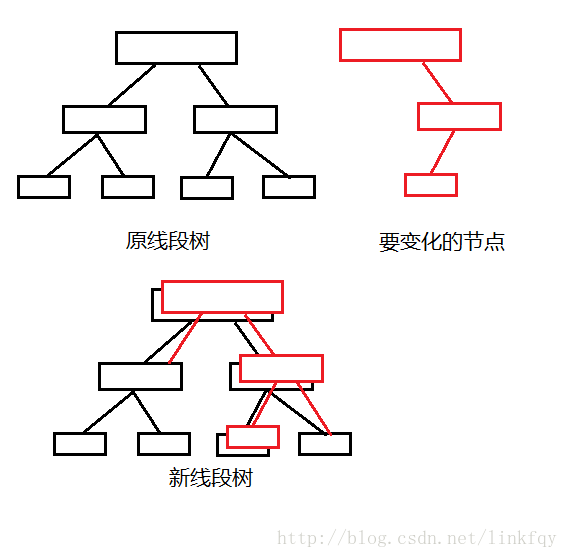
新的节点“依附”在旧的线段树上，并与旧的线段树共用一些子树
（看这图需要有一点空间想象力）
另外，主席树有一个很有用的性质就是每棵线段树的形态都是一样的，所以可以对每个对应节点相加减（这样就可以容斥啦）

【应用】

可持久化线段树有什么用呢？一般用于基于序列的名次操作（离线）。
说个最简单的，给定一个序列，每次询问区间[L,R]中第k大的数。
首先考虑线段树表示的是什么，我们定义线段[L,R]表示所有满足L<=a[i]<=R的个数（注意不要和上面的区间[L,R]搞混）。
那么思考如下过程：从1至n，一个一个对线段树插入a[i]。
这样就可以构造出主席树。其中第i棵线段树（第i个历史版本）rot[i]的节点[L,R]的权值表示[1,i]这个子区间的所有满足L<=a[i]<=R的个数。
询问与BST的Rank操作类似，考虑在rot[i]中找第K大的数，如果左子树的权值大于等于K，说明第k大的在左边，否则在右边，并修改K的值。这样询问rot[R]和rot[L-1]两次即可得到答案。（实际运用中我把两次询问做到了一起）

【例题】

POJ 2104
裸题，按照我上面写的做就行了

#include
#include
using namespace std;
const int maxn=100005,maxs=2000005;
int n,m,q,a[maxn],b[maxn];
struct node{
    node *l,*r;
    int s,L,R;
    node(int x=0,int y=0) {L=x;R=y;s=0;}
    void pushup() {s=l->s+r->s;}
}base[maxs],nil;
typedef node* P_node;
P_node null=&nil,len=base,rot[maxn];
void Seg_T_init(){
    null->l=null->r=null;
}
P_node newnode(int l,int r){
    *len=node(l,r);
    return len++;
}
P_node build(int l,int r){
    P_node x=newnode(l,r);
    if (l==r) return x;
    int mid=l+r>>1;
    x->l=build(l,mid);x->r=build(mid+1,r);
    x->pushup();
    return x;
}
P_node ist(P_node lst,int k){
    P_node x=newnode(lst->L,lst->R); x->s=lst->s;
    x->l=lst->l; x->r=lst->r;
    if (x->L==x->R) {x->s++;return x;}
    int mid=x->L+x->R>>1;
    if (k<=mid) x->l=ist(lst->l,k);else
     x->r=ist(lst->r,k);
    x->pushup();
    return x;
}
int qry(P_node l,P_node r,int k){
    if (l->L==l->R) return b[l->L];
    int tem=r->l->s-l->l->s;
    if (k<=tem) return qry(l->l,r->l,k);else return qry(l->r,r->r,k-tem);
}
inline int red(){
    int tot=0,f=1;char ch=getchar();
    while (ch<'0'||'9'if (ch=='-') f=-f;ch=getchar();}
    while ('0'<=ch&&ch<='9') tot=tot*10+ch-48,ch=getchar();
    return tot*f;
}
int main(){
    Seg_T_init();
    n=red(),q=red();
    for (int i=1;i<=n;i++) a[i]=b[i]=red();
    sort(b+1,b+1+n);
    m=unique(b+1,b+1+n)-b-1;
    rot[0]=build(1,m);
    for (int i=1;i<=n;i++)
     rot[i]=ist(rot[i-1],lower_bound(b+1,b+1+m,a[i])-b);
    while (q--){
        int l=red(),r=red(),k=red();
        printf("%d\n",qry(rot[l-1],rot[r],k));
    }
    return 0;
}