Part 13 (1) Fourier级数基本概念与应用

1. Fourier级数基本概念

1.1. 概念准备

1.1.1. 三角函数系的正交

$${\int }_{-\pi }^{\pi }\cos mx\cos nx\mathrm{d}x=\{\begin{array}{ll}0,& m\ne n\\ \pi ,& m=n\ne 0\\ 2\pi ,& m=n=0,\end{array}m,n=0,1,2\cdots$$
$${\int }_{-\pi }^{\pi }\sin nx\sin mx\mathrm{d}x=\{\begin{array}{ll}0,& m\ne n\\ \pi ,& m=n\end{array}m,n=1,2,\cdots$$
$${\int }_{-\pi }^{\pi }\sin nx\cos nx\mathrm{d}x=0,m=0,1,2\cdots ,n=0,1,2\cdots$$
利用和差化积即可。

注意推导中一个常用的想法是：几倍于$2\pi$周期的三角函数，在${\int }_{-\pi }^{\pi }$上积分为0.

1.1.2. 一种特殊的函数项级数——三角级数

$$\frac{a_0}{2}+\sum _{k=1}^{\infty }\left(a_k\cos kx+b_k\sin kx\right)$$

1.1.3. 分段分析性质

• 分段连续：闭区间上除去有限个第一类间断点外处处连续
• 分段单调：闭区间上只有有限个单调区间
• 分段可导：分段连续，且在这些间断点上左右广义导数存在

例 广义右导数：其中$f(x_0+0)$为右极限
$$\underset{\Delta x\to 0+0}{\lim }\frac{f(x_0+\Delta x)-f(x_0+0)}{\Delta x}$$

分段（一阶）光滑：分段连续，导数分段连续，分段可导，那么分段光滑

分段光滑函数的性质：

1. $f(x)$在$[a,b]$上可积
2. $f^{\prime }(x)$在$[a,b]$上可积

1.2. Fourier系数

欲求$a_k,b_k$，我们利用三角函数正交性的几个理论结果，我们对三角级数两侧分别乘$\cos kx,\sin kx$得到
$$\begin{gathered} a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos nx\mathrm{d}x,(n=0,1,2\cdots ) \\ {b}_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\sin nx\mathrm{d}x,(n=1,2\cdots ) \end{gathered}$$

1.3. 可以展成Fourier级数的条件

两种Dirichlet条件：

• 分段连续且分段单调
• 分段光滑

（逐点收敛定理）Dirichlet定理：满足Dirichlet条件的函数可以展成Fourier级数。
或者说其对应Fourier级数收敛到该点的广义左右极限的平均值$$\frac{f(x-0)+f(x+0)}{2}$$

此时，前$n$项和函数为
$$S_n(x)=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x+t)\frac{\sin (n+\frac{1}{2})t}{2\sin \frac{1}{2}t}\mathrm{d}t$$
这个积分称为Dirichlet积分。

1.4. Fourier级数的性质

（系数的趋势）设$f(x)$在$[-\pi ,\pi ]$上可积或绝对可积，则其Fourier系数满足：
$$\underset{n\to \infty }{\lim }{a}_n=0,\underset{n\to \infty }{\lim }{b}_n=0$$

（Fourier级数的逐项积分定理）$\forall x,c\in [-\pi ,\pi ]:$
$${\int }_c^{x}f(t)\mathrm{d}t={\int }_c^x\frac{a_0}{2}\mathrm{d}t+\sum _{n=1}^{\infty }\left(a_n{\int }_c^x\cos nt\mathrm{d}t+b_n{\int }_c^x\sin nt\mathrm{d}t\right)$$
这表明即便是$f(x)$的Fourier级数不收敛，它的逐项积分收敛到$f(x)$的积分，这是Fourier积分的特有性质

1.5. 题型：Fourier级数的展开计算

• Step1：分析函数是否满足Dirichlet条件
• Step2：计算Fourier系数
• Step3：分间断点和连续点讨论Fourier级数表达式

1.5.1. 常用化简结构：

$${\int }_0^{\pi }x\cos nx\mathrm{d}x=\frac{1}{n^2}\cos nx{|}_0^{\pi }=\frac{1}{n^2}\left[(-1{)}^n-1\right]$$
$${\int }_0^{\pi }x\sin nx\mathrm{d}x=-\frac{\pi }{n}(-1{)}^n$$

1.5.2. 拓展题型

1.5.2.1. 不以$2\pi$为周期

在计算的时候，将原问题中的$\frac{1}{\pi }$换成$\frac{2}{T}$或表示成$\frac{1}{l}$

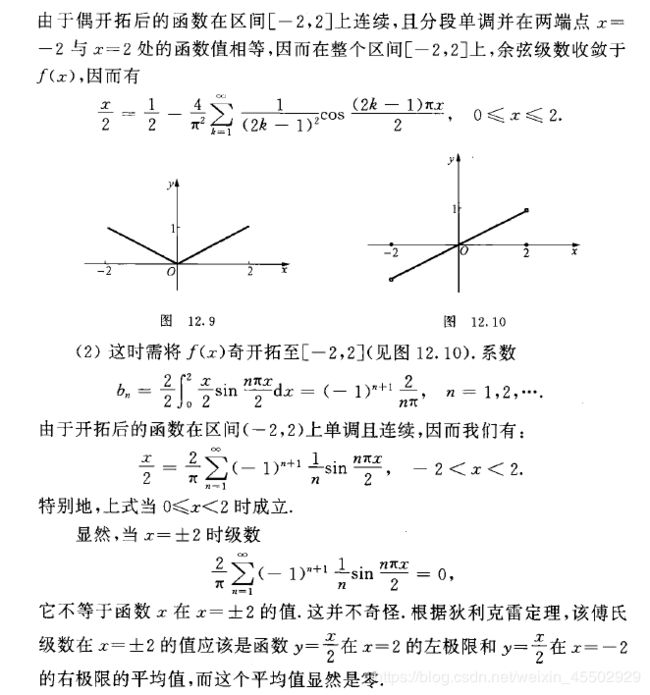
1.5.2.2. 奇偶延拓

区间形如$[0,l]$的任意函数，都可以通过延拓构造出类似周期函数的结构，这样就可以使用Fourier级数展开。随后将定义域缩小即可。
在数学物理方法中，这称作半幅Fourier级数。除了通常的奇延拓(对应半幅正弦级数)和偶延拓
$$\varphi (x)=\sum _{n=1}^{\infty }{C}_n\sin \frac{n\pi x}{L}=D_0+\sum _{n=1}^{\infty }{D}_n\cos \frac{n\pi x}{L}$$
之外，还可以有非整数系数的三角级数：
$$\varphi (x)=\sum _{n=1}^{\infty }{C}_n\sin \frac{(2n+1)\pi x}{2L}$$
这在有限区间尤其是边值问题当中有广泛应用。
例题：

这个例题综合了这两个拓展问题，值得研究