FP-growth算法——原理
之前我们已经可以使用Apriori算法来在一个数据集里面找出那些支持度较高的元素
组合,我们来回顾一下Apriori算法的核心。
Apriori算法的核心其实就是分三步:
1.在现有组合的基础上,生成可能的元素组合类型
2.遍历数据集,求得这些元素组合的支持度(频率)
3.剪枝,除去支持度不符合条件的组合。
这三步迭代即可。其中在剪枝的过程中使用到了Apriori原理来进行剪枝,而Apriori的数学原理为积事件的概率小于等于每个事件分别发生的概率。
虽然有剪枝大法,但是Apriori算法依然很高。如果实际有M个组合需要计算其支持度的话,那我们可能要遍历M次整个数据集才行。FP-growth正是一种高效的找出频繁项集的算法,他只需要遍历两次数据集即可。
FP-算法使用了一种叫做FP(Frequence parttern )的树结构。FP树的每个节点记录了该节点上的元素的频率,树的分支只有在没有匹配时才分支。
FP树节点的定义:
count :元素出现的次数
nodelink :链接到下一个相似节点(name相同)
parent :该点的父节点
children :叶子节点
FP建树过程
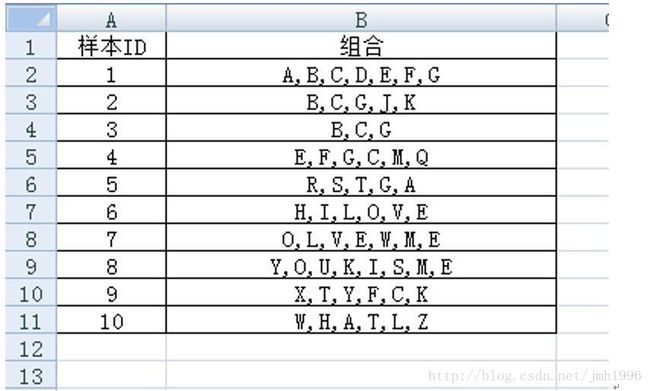
假设数据集如下:
其中A,B,C,D···表示基本元素。
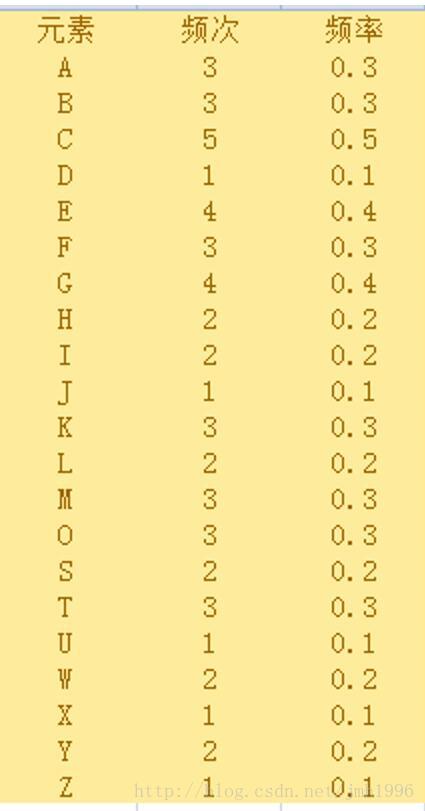
1.首先我们扫描一遍数据集,计算各基本元素出现的频次和频率。
假设我们设置的支持度阈值为0.3,小于0.3的都直接丢掉了。
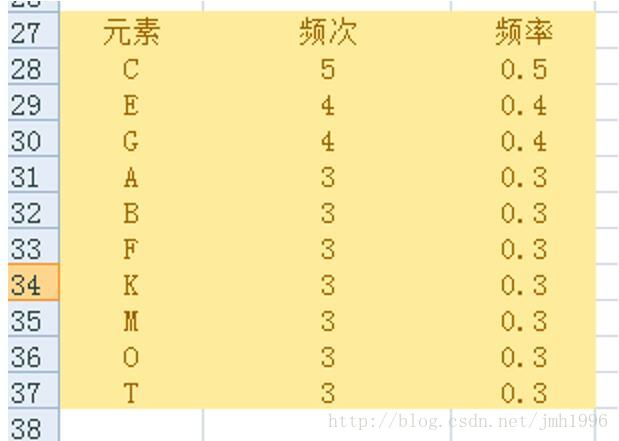
那么只剩下这些基本元素:
我们把剩下的元素按频率从高到低排序:
改正(E的频次应该为5)
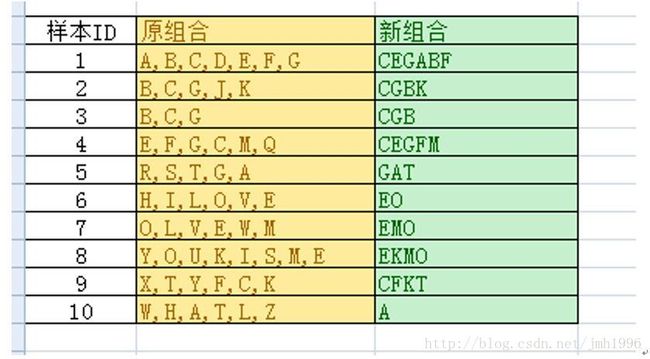
同时将原始数据集做修改,只保留剩下的高频率元素,而且每个样本中元素的排列是按元素的频率高低来出来的。比如样本1:
| 1 | A,B,C,D,E,F,G |
|---|
修改为:C,E,G,A,B,F因为元素D的频率太低了所以被删除了。
用类似的方法,数据集将变成:
2.然后我们再遍历一次新的数据集,生成FG树。
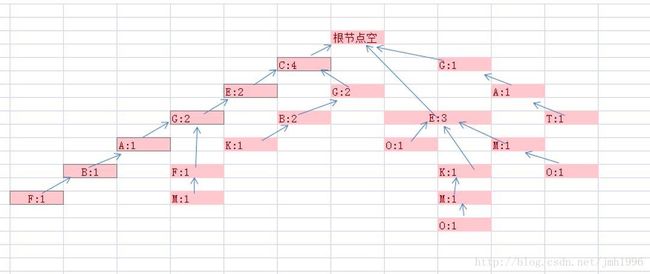
FG的根结点为空集。在建树的过程与字典树类似,用输入作为路径依次跟各层的节点匹配,如果发现在这条路径下该层中有未匹配的元素,则在上一个已匹配的元素的基础上新建一个结点。新结点的父结点是树上最后一个已匹配的结点,结点的count为1,name为元素名,子节点为None,linknode也为none。下面我们显示建树的过程:
初始的时候FP树为空。
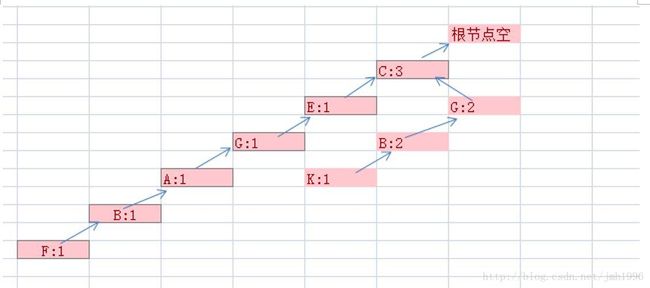
1.输入:CEFABF
一开始FP为空,所以遇到输入串的第一个C时,没有任何匹配,于是新建立一个节点C它的count为1.父结点为第一级的根节点。
然后现在处理输入的第二个元素E.我们发现从{根}->{C}下来,第二层没有节点去匹配E,于是在第二层新建一个节点E:1.其父结点为上一次C.
以此类推,最后FP变为:
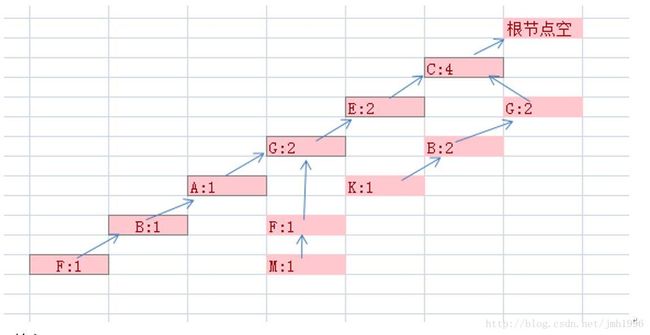
2.输入CGBK
输入的第一个元素为C,我们看FP树从根出发的第一层已经有C结点,于是这个C结点的count增加1.
输入的第二个元素为G,从走过的C结点向下走,发现C的子结点并没有G结点,于是新建一个G节点。
输入的第三个元素为B,从刚刚走过的{C}-》{G}下来,并没有B结点,于是新建。
···
最后FP变成:
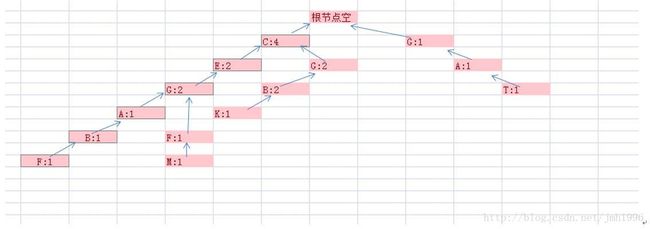
3.输入CGB
输入的第一个元素为C,从根出发,有一个C结点 ,所以C的count增加1.变成3
输入的第二个元素为G,从{根}->{C}过来,发现有一个G节点,所以G的count增加1,变成2
输入的第三个元素为B,从{根}->{C}->{G}过来,发现有一个B节点,所以B的count增加1,变成2
最后FP变成:
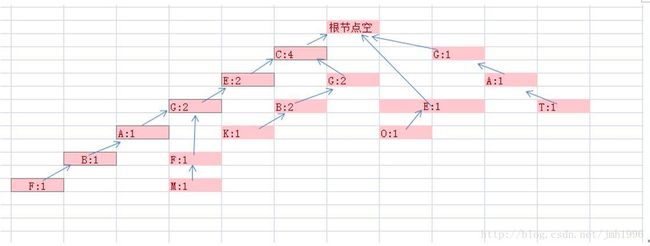
4.输入CEGFG.
与上面的过程类似,FP变成:
5.输入GAT
FP变成:
6.输入EO
FP变成:
7.输入EMO
8.输入EKMO
9.输入CFKT
10.输入A
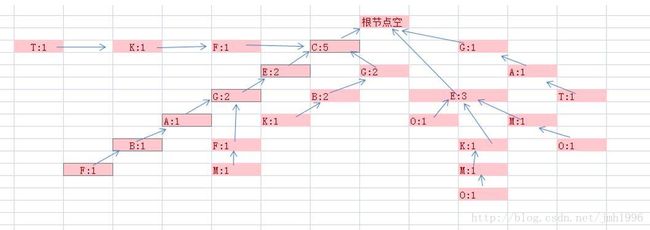
可以看出:
对于输入 {e1,e2,e3,…,en} ,我们的目标是在FP树上找到或生成一条从根出发,依次经过 {e1,e2,e3,…,en} 的路径,如果遇到不存在的节点则建立新节点,如果存在则增加该节点的count域。
现在,我们用一棵树来表示刚才的数据集,通过这棵树我们的查找效率将快的多。这树数的表现能力其实就是等于刚刚的数据集的。
有了这颗FP,我们可以判断某个项集是否频繁了。
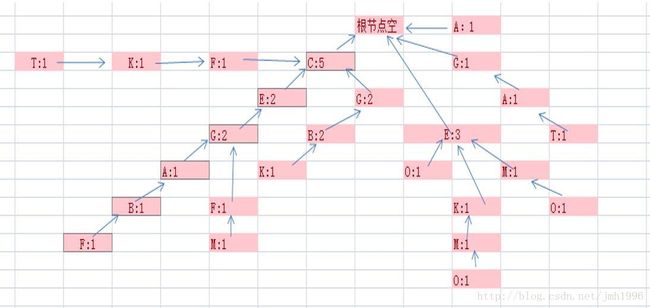
例如,计算{C,G}的频率,判断{C,G}是否频繁。
首先 我们按照基本元素频率的大小对{C,G}里的元素进行排序:{C,G}->{C,G}
接着,我们以排序好的项集的最后一个元素G为起点,在FP树中找到所有的G节点,发现共有3个。接着,我们从每个G出发,向父节点迭代,直到所走的路径包含{C,G}或到达根节点。我们记录下那些所走路径可以覆盖{C,G}的G节点,将这些G节点的count相加的即是项集{C,G}的频次。
例如:对于所有的3个G节点,共可以生成三条路径:{G,C},{G,F,C}以及{G}。其中只有{G,C}和{G,F,C}覆盖了目标。这两条路径的G点的和为2+2=4.所以{C,G}的频率为4/10=0.4 大于0.3的阈值,因此是频繁的。
又比如:判断{G,C,Y}是不是频繁的。
这东西在排序的过程中就会发现Y的频率太低,已经被排除在外,所以{G,C,Y}绝逼不是频繁项集。事实上{G,C,Y}在原数据集出现0次,根本就没这种组合来的。
所以我们可以在Apriori的基础上,用Apriori原理生成候选项集,然后把每次计算某个项集是否频繁 改成在FP树上操作,而不是再去遍历整个数据集,这样的确可以加速很多!
但是!FP-growth 不止这么厉害。
它不仅可以加速判断某个项集是否频繁,还能加速频繁项集的生成!
这么做呢?
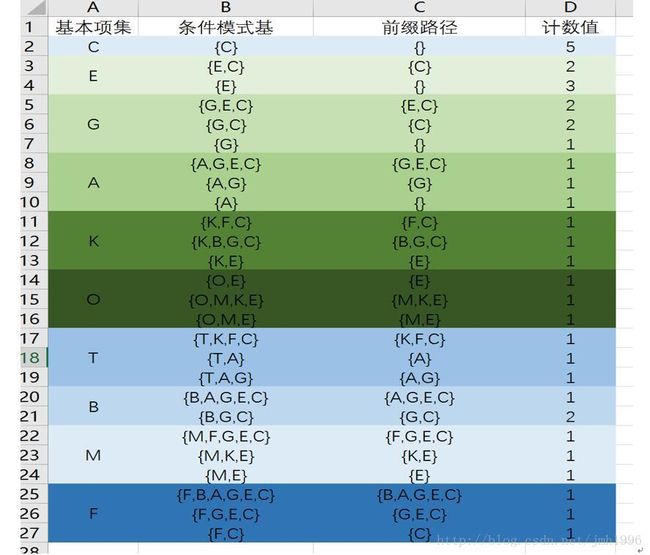
这是我们得到的FP树,现在我们提出条件模式基的概念。这个概念很好理解,其实上面在利用FP计算某个项集是否频繁就已经用到了条件模式基的思想了。
条件模式基是指在FP树中以所查找元素项为结尾的路径集合。例如G的条件模式基就是{{G,C},{G,E,C},{G}}.而条件模式基中每条路径除去G本身剩下的路径被称为前缀路径。每个条件模式基的元素都与一个计数值相关。这个计数值就是该路径的起点的计数值。
例如:G的条件模式基为{G,C},{G,E,C}和{G},它们的计数值分别为2,2,1。计数值说明了在这条路径下该项集出现的次数。
同理我们可以整理出所有基本频繁项集的前缀路径和对应的计数值。
然后我们再以某个元素的前缀路径为数据集(空集除外),为这个元素建立一颗条件FP树。条件FP树也是FP树,依然进行这个过程,直到FP所有元素都处理好为止。
以G为例子:
G的前缀路径:{E,C},{C},他们的计数值分别为2,2。
可知在条件树中,其中E的频率为0.2,这个频率的含义其实是指{G,E}的频率为0.2,这个值小于阈值0.3,于是E被排除了。那就只剩下C了。
而C在条件树中的频率为0.4,满足条件,然后基于C再构造G的条件树下的C的条件树,这时发现条件树的元素没了。故而对于G来说,它只有{G,C}这个项集是频繁的。
OK,讲了这么多,接下来,我们就来看看如何编程实现FP-growth算法。