数据探索、数据清洗学习笔记

1.说明

1. 该学习笔记仅供个人学习使用，不代表任何官方指导或意见。

2. 该学习笔记为个人原创，转载请征得博主同意，或声明原文链接。

3. 有需要其他资料或有其他问题可私信或者加qq2356081476，这不是我的义务但也欢迎各位朋友与我讨论相关问题，共同进步。

4. 错字，语法，排版等问题请见谅。

5. 这一条是和后来加上来的，建议先看目录中的小结部分，因为笔记是做着做着笔者自己也有一些体会和理解，这些一般我就放到小结部分去了。但是千万别觉得看了小结就相当于看了全文了，理解需要逐步深入。

2.作文目的

2020年寒假有试题研究风电功率分析及波动分析。其中有需要学习数据探索、数据清洗、回归分析等问题。在各大网站（如CSDN、知乎、知网、百度）所查资料较为松散，故作此学习笔记以适用个人学习及复习。

3.数据探索

3-1.定义

对样本数据集的整体结构和规律特征进行分析的过程。

3-2.意义

1. 有助于选择数据清洗方法。
2. 有助于选择合适建模方法。

3-3.方法

通过检验数据集的数据质量、绘制图表、计算某些特征量等手段。及数据质量分析，数据特征分析两种。

3-3-1.数据质量分析

3-3-1-1.定义

检查原始数据中是否存在“脏”数据。
脏数据一般是指不符合要求， 以及不能直接进行相应分析的数据。在常见的数据挖掘工作中， 脏数据包括如下内容（排名不分先后）。
1.缺失值 2.异常值 3.不一致的值

• 缺失值：
  顾名思义，数据集中没有的，缺失的值。
• 异常值：
  对客观事物、业务等已有的认识，判别由于外界干扰、人为误差等原因造成实测数据偏离正常结果。
  例如：
  人的年龄300岁，已经属于远超认知。或者是个负值，完全不符合客观事物。
• 不一致的值
  简单理解为前后矛盾，有冲突。如果一张表连续前后给了两次，可能就会出现。
  例如：
  ①.有一处$a=10$，另外一处$a=100$
  ②.调查对象说自己开车上班，又报告没有汽车。

3-3-1-2.意义

1. 是分析数据中有效数据准备过程中的一个重要环节。
2. 是数据清洗的前提。
3. 是为数据挖掘的分析的有效性和准确性的基础。
   注：
   1. 数据质量分析的意义与数据探索的意义界限模糊，建议集中记忆。

3-3-1-3.判别（分析）方法

对脏数据（3种）的判别。
注意每用以下方法判断出所有异常值后，修改其中之一后要重新计算得到的二次的所有异常值才能进行二次修改。就是说不能修改了一个之后接着修改第二个。

3-3-1-3-1.异常值判别：

在异常值的定义的例子中是我们客观很容易就能看见异常值，这些很容易判别。有时候就会碰到很难判别的异常值。人类年龄300岁很容易看出来，200岁也很容易。100岁呢，这就不一定了。假如在数据集中90-110岁的人不少，那可能100岁不是异常的。假如数据集中90-110岁的人很少，就ta100岁的老者一位。那可能就是异常值。显然一群年轻人中站着一位老者不太”正常“。这就需要我们用一些数学统计的方法。

Ⅰ.3σ准（原）则
注意条件：数据服从于正态分布¹。如果不满足此条件结果未必可信。
简述：某个值远离平均值三倍标准差，那么这个值是异常值。
数学公式：|x-μ|>3σ
其中x表示某个值，μ表示平均值，σ表示标准差。

Ⅱ.箱形（型）图
注意条件：无。
按下述步骤画出一个箱型图：
①.将所有数据从小到大排序。设有n个数据。
②.$\frac{n}{4}$取整所在的值为下四分位设为L。
③.$3\times \frac{n}{4}$取整所在的值为上四分位设为U。
④.上下四分位的差设为IQR，即IQR=U-L
⑤.上界设为 U + 1.5IQR = 2.5U - 1.5L，下界设为 L - 1.5IQR = 2.5L - 1.5U
不在上界和下界之间的值为异常值。

Ⅲ.其它方法(前两种方法更为常用，所以其它方法不做笔记，之后有需要再做研究)
①.肖维勒准则（等概率准则）
②.格拉布斯准则
③.狄克逊准则
④.T检验

3-3-1-3-2.缺失值判别：

这一部分判别很简单，作者从各处了解学习，建议先以下这样做对之后改善缺失值有帮助。

①.数据不用作排序，对数据做分片处理。如n个数据，每100个作为一片。
②.对每一片做重要性与缺失率评估。
③.双低区不做处理或者以平均值填充。
④.双高区域以图中三种方法填充，具体在数据清洗条目中。
⑤.重要而低缺失率区以以图中三种方法填充，具体在数据清洗条目中。
⑥.不重要而高缺失率区去掉（删除）。

3-3-1-3-3.不一致值的判别：

不一致数据的产生主要发生在数据集成的过程中，这可能是由于被挖掘数据是来自于从不同的数据源、对于重复存放的数据未能进行一致性更新造成的。如果直接给出了数据表，要求分析，没有看到过程的这种一般不会有不一致的值。

3-3-1-4.改善方法

后经发现，改善方法应该就是数据清洗的条目，所以所有改善方法就转写到数据清洗条目。

3-3-2.数据特征分析

要知道什么是数据特征分析，就要先知道什么是数据特征。虽然没有查到资料严格的说明定义它，但是却有数据特征分析的介绍说明。

说明如下：通过绘制图表，计算等手段进行数据的特征的分析。主要通过分布分析、对比分析、统计量分析、周期性分析、贡献度分析、相关性分析等角度进行展开。

所以我认为数据特征，指的是数据的“分布”、“统计量”、“周期性”、“相关性”、‘贡献度’等等，在以下目录会详细研究说明。

3-3-2-1.意义

也没有查到相关资料有介绍数据特征分析的意义，但是笔者也估计与前二者的意义大同小异。

3-3-2-2分布分析

以我所查资料，数据的分布主要指的是频率分布表、频率分布直方图、茎叶图、散点图、饼图。所以分布分析也就是分析数据的频率分布表、频率分布直方图等。

对于定量数据的分布分析和定性数据的分布分析又有所不同。

3-3-2-2-1.定量数据的分布分析

Ⅰ.定量数据的分析是做频率分布直方图，一般按照以下步骤进行：

1. 求极差：
   极差=最大数据值-最小数据值。
2. 决定“组距”与“组数”：
   组距设为d自己确定，一般建议2-3。然后取开区间(a,b)，使最大值和最小值落在开区间(a,b)内，a略小于样本数据的最小值，b略大于样本数据的最大值
   $组数=\frac{b-a}{组距}$
3. 决定分点：
   分点指每组的两端端点值。
   各数据组的边界范围按左闭右开区间，如
   [a,a+d），[a+d,a+2d),……[a+(m-1)d,b)

例子：1w个数据，值在0-200间，组距为2。取（-1，201）
可得：组数为101，第一组分点为-1和1，第二组分点为1和3，…，第一百零一组分点为189-201。

4. 列出频率分布表：
   统计落在每组的数据的个数，可得每组的频数和频率。
5. 画频率分布直方图：
   横轴为组，纵轴为$\frac{频率}{组距}$，直方图每组面积为每组频率。所有组面积和为1

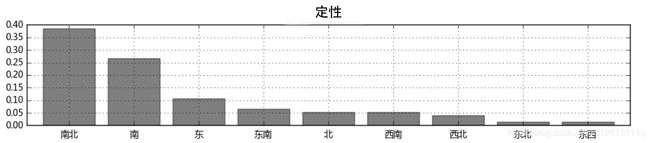
3-3-2-2-2.定性数据的分析：

与上定量数据分析类似做 频率分布直方图，最终横轴不是组而是定性的数据。

定量数据频率分布直方图（上）与定性数据频率分布直方图（下）对比

3-3-2-3.对比分析

以下一段是其他博友的定义。截自这里
对比分析是指把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小，水平的高低，速度的快慢，以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中，选择合适的对比标准是十分关键的步骤，只有选择合适，才能做出客观的评价，选择不合适，评价可能得出错误的结论。

对比分析包括绝对数比较和相对数比较。两者之间的定义就笔者所查资料还比较模糊。且绝对数比较没有具体化和例子，而相对数有例子，可以加深理解。

1. 绝对数比较：
   利用绝对数进行对比，从而寻找差异的一种方法。
2. 相对数比较：
   由两个有联系的指标对比计算，反映客观现象之间数量联系程度的综合指标，其数值表现为相对数。相对数比较又分为以下几种:
   ①.结构相对数
   如居民食品支出额占消费支出总额比重、产品合格率等这样将同一总体内的部分数值与全部数值对比求的比重。来说明事物的性质、结构或质量。
   ②.比例相对数
   如男女的人口性别比例、投资与消费比例等将同一总体内不同部分的数值进行对比。来表明总体内各部分的比例关系。
   ③.比较相对数
   如不同地区商品价格对比，不同行业、不同企业间某项指标对比等这样将同一时期两个性质相同的指标数值进行对比。来说明同类现象在不同空间条件下的数量对比关系。
   ④.强度相对数
   如人均国内生产总值用“元/人”表示，人口密度用“人/平方公里”表示这样将两个性质不同但有一定联系的总量指标进行对比。用以说明现象的强度、密度和普遍程度。
   ⑤.动态相对数：
   如一批货物30天每天的销售情况这样将同一现象在不同时期的指标数值进行对比。来说明发展方向和变化的速度。

3-3-2-4.统计量分析

对数学知识有一定了解的应该知道统计量指均值、方差、中心距、原点矩等。
统计量分析指用统计指标对定量数据进行统计描述。常从集中趋势和离中趋势两个方面进行分析。反映平均水平的指标是对个体集中趋势的度量，使用最广泛的是均值和中位数;反映变异程度的指标则是对个体离开（离散）平均水平的度量，使用较广泛的是标准差(方差)、四分位间距。

1. 集中趋势度量如均值、中位数、众数
2. 离中趋势度量如极差、标准差
3. 变异系数
   变异系数度量标准差相对于均值的离中趋势，变异系数主要用来比较两个或多个具有不同单位或不同波动幅度的数据集的离中趋势。怎么确定计算变异系数？这个自己去查一下百度百科都有，我的试题没有用到这一块就不仔细研究了。
4. 四分位数间距
   上文有介绍四分位数（分上和下），不再赘述。这里说一下其意义：
   上四分位数与下四分位数之差，其值越大，说明数据的变异程度越大;反之，说明变异程度越小。

3-3-2-5.周期性分析

高中时期就已经学过周期函数了。顾名思义，就是分析数据是否有周期性。

相对较长的周期性趋势有年度周期性趋势、季节性周期趋势。
相对较短的有月度周期性趋势、周度周期性趋势，甚至更短的天、小时周期性趋势。

3-3-2-6.相关性分析

分析连续变量之间线性相关程度的强弱，并用适当的统计指标表示出来的过程称为相关分析。
在二元变量的相关分析过程中比较常用的有pearson相关系数、spearman秩相关系数和判定系数。具体不再细究，有兴趣参考这里。
注:
笔者不确定没有线性相关的是不是就不要进行相关性分析。像笔者的试题数据画出来非常复杂。

3-3-2-7.贡献度分析（帕累托分析）（ABC分类法）（二八定律）

贡献度分析又称帕累托分析，它的原理是帕累托法则，又称20/80定律、80/20定律、二八定律。

一个简单例子：世界上80%的人掌握20%的财富，20%的人掌握80%的财富。
简单介绍定义就是：相对来说数量较少的原因往往造成绝大多数的问题或缺陷。做20%的事可以产生整个工作80%的效果的法则。

这一条目搜索百度解析都较为详细，我想更别说CSDN上的博文了。暂时不做深入研究。

3-4.小结

1. 数据探索是对数据的整体（结构和规律）和部分=的分析。分别对应于
   数据特征分析和数据质量分析。
2. ”数据质量“就是看部分甚至是个别数据”脏“与否，脏的我们就不要他，或者改变他。判断的方法有几种，不要或者改变的方法也有几种。注意条件。
3. ”数据特征“就是看整体。如中位数，众数，平均数，周期等等。
4. 随着数据量的增大，异常值和缺失值对整体分析结果的影响会逐渐变小，因此在“大数据”模式下，数据清洗可忽略异常值和缺失值的影响，而侧重对数据结构合理性的分析。可以借助于贡献度分析，以较少的清洗取得较为显著的效果。

4.数据清洗

补充说明
1. 异常值处理，先按照3-3-1-3-2.缺失值判别法作出重要性缺失率图，对应四个区域应用不同的处理方法。
2. 不一致的值处理，这个笔者没有查到资料确切说明处理方法。建议也作重要性缺失率图。重要性低删除，重要性高取所有不一致的值的平均来代替。

4-1.定义

把在数据探索中数据质量分析中的脏数据改善甚至去除的过程。

4-2.意义

是整个数据分析过程中不可缺少的一个环节，其结果质量直接关系到模型效果和最终结论。
注：经过了这么几天的研究，上述后半句感觉不太恰当。见3-4 小结的第4条。

4-3.方法

方法有很多种，笔者简单归类为三种：不处理、简单处理、复杂处理（非专业名词）。
在下文将不做不处理的介绍，字面意思。
注：做所有处理前建议备份数据！！！

4-3-1.简单处理

包括删除和平均值填充（平均值填充有时候也可以用众数填充，中位数填充，这还得看数据k距离范围内的一些数据分布情况，最好还是用平均值填充，用的也多一些）。注意删除有的地方是单个数据值的删除，有的地方是数据片段的删除。我应该会提到。

4-3-2.复杂处理（非专业名词）

复杂处理只是笔者相对于简单处理作的一个名字，步骤上也的却复杂了些许。包括k最近距离、回归、多重插补、极大似然四个方面，其中极大似然暂不做研究。

4-3-2-1.k最近邻算法（k最近距离法）

近朱者赤，近墨者黑。这句话大家应该都知道，k最近距离法的思路就类似于它。
先介绍两个例子：

1. 一个未知水果，要判断它是什么。按照近朱者赤原则，就是看他附近k距离内的哪个水果多，他就是哪个。
2. 一个人，要知道ta是什么职业。就看ta的朋友大多是什么职业。

就数据（数值）方面来说，假如一个值（异常、缺失、不一致）是我们要改善的，先取一个距离²k，然后得若干个距离k内得数据，取这若干个数据的加权平均值来估计缺失数据值。

4-3-2-2.回归

基于完整的数据集或者需要改善的数据附件的数据， 做拟合处理，建立回归方程。以回归函数值改善。试题之后会有需要用到这一板块估计，到时候单独作一个学习笔记，这里先不作仔细研究。

4-3-2-3.多重插补法

就老师所给ppt来看，简单介绍多重插补法如下：
由包含m个插补值的向量代替一个待改善的值，然后对于m个插补值，一次填充并进行试探。最终选出一个最好的插补值。
具体步骤与方法暂不作研究。

4-3-2-4.极大似然法

暂不作研究。

4-4小结

1. 数据清洗完后不是直接进行下一阶段，而是反复继续数据探索。下一节也有说明。
2. 再次提醒，做所有处理前先做数据备份。
3. 数据处理、数据预处理、数据清洗的区别与关系：
   查过这么多资料，各有所不同，笔者在这里归结为数据处理>>数据预处理>数据清洗

5.数据探索与数据清洗的联系

在整个数据分析的过程种。二中紧密相关，不可分隔。数据清洗和数据探索通常交互进行。
开始进行第一步数据探索，下一步就是数据清洗，再接着数据探索，以此循环。直到数据满足没有脏数据或脏数据较少等以及其他条件。
笔者老师的ppt上有以下两段话：

1. 数据探索有助于选择数据清洗方法
2. 数据清洗后可以更有效的进行数据探索

6.注释部分

---

1. 服从正太分布的判别方法：W检验、D检验，暂时不做笔记
   ，之后做研究。 ↩︎

2. 这个距离指欧式距离。
   欧式距离： $$d=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$
   欧氏距离在二维和三维上就是我们熟悉的距离公式。上述公式为n维的情况下
   。 ↩︎