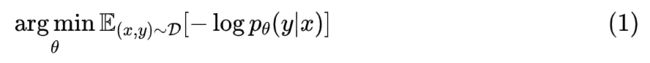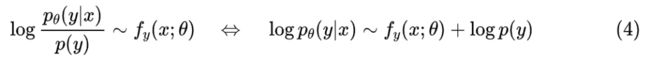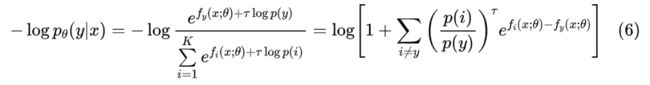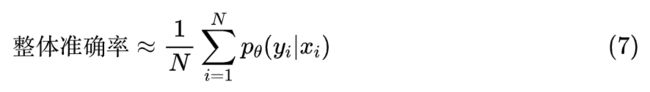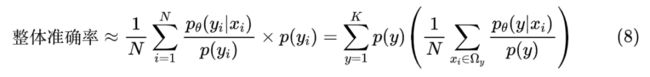通过互信息思想来缓解类别不平衡问题
©PaperWeekly 原创 · 作者｜苏剑林
学校｜追一科技
研究方向｜NLP、神经网络
类别不平衡问题，也叫“长尾问题”，是机器学习面临的常见问题之一，尤其是来源于真实场景下的数据集，几乎都是类别不平衡的。大概在两年前，笔者也思考过这个问题，当时正好对“互信息”相关的内容颇有心得，所以构思了一种基于互信息思想的解决办法，但又想了一下，那思路似乎过于平凡，所以就没有深究。
然而，前几天在 arxiv 上刷到 Google 的一篇文章 Long-tail learning via logit adjustment [1]，意外地发现里边包含了跟笔者当初的构思几乎一样的方法，这才意识到当初放弃的思路原来还能达到 SOTA 的水平。于是结合这篇论文，将笔者当初的构思过程整理于此，希望不会被读者嫌弃“马后炮”。
问题描述
这里主要关心的是单标签的多分类问题，假设有 共 K 个候选类别，训练数据为 ，建模的分布为 ，那么我们的优化目标是最大似然，或者说最小化交叉熵，即：
通常来说，我们建立的概率模型最后一步都是 softmax，假设 softmax 之前的结果为 （即 logits），那么：
所谓类别不均衡，就是指某些类别的样本特别多，就好比“20% 的人占据了 80% 的财富”一样，剩下的类别数很多，但是总样本数很少，如果从高到低排序的话，就好像带有一条很长的“尾巴”，所以叫做长尾现象。
这种情况下，我们训练的时候采样一个 batch，很少有机会采样到低频类别，因此很容易被模型忽略了低频类。但评测的时候，通常我们又更关心低频类别的识别效果，这便是矛盾之处。
常见思路
常见的思路大家应该也有所听说，大概就是三个方向：
1. 从数据入手，通过过采样或降采样等手段，使得每个 batch 内的类别变得更为均衡一些；
2. 从 loss 入手，经典的做法就是类别 y 的样本 loss 除以类别出现的频率p(y)；
3. 从结果入手，对正常训练完的模型在预测阶段做些调整，更偏向于低频类别，比如正样本远少于负样本，我们可以把预测结果大于 0.2（而不是 0.5）都视为正样本。
Google 的原论文中对这三个方向的思路也列举了不少参考文献，有兴趣调研的读者可以直接阅读原论文，另外，知乎上的文章《Long-Tailed Classification (2) 长尾分布下分类问题的最新研究》[2] 也对该问题进行了介绍，读者也可以参考阅读。
学习互信息
回想一下，我们是怎么断定某个分类问题是不均衡的呢？显然，一般的思路是从整个训练集里边统计出各个类别的频率 p(y)，然后发现 p(y) 集中在某几个类别中。所以，解决类别不平衡问题的重点，就是如何把这个先验知识 p(y) 融入模型之中。
在之前构思词向量模型（如文章《更别致的词向量模型(二)：对语言进行建模》[3]）的时候，我们就强调过，相比拟合条件概率，如果模型能直接拟合互信息，那么将会学习到更本质的知识，因为互信息才是揭示核心关联的指标。
但是拟合互信息没那么容易训练，容易训练的是条件概率，直接用交叉熵 进行训练就行了。所以，一个比较理想的想法就是：如何使得模型依然使用交叉熵为 loss，但本质上是在拟合互信息？
在公式 (2) 中，我们是建模了：
现在我们改为建模互信息，那么那也就是希望：
按照右端的形式重新进行 softmax 归一化，那么就有：
或者写成 loss 形式：
原论文称之为 logit adjustment loss。如果更加一般化，那么还可以加个调节因子 ：
一般情况下， 的效果就已经接近最优了。如果 的最后一层有 bias 项的话，那么最简单的实现方式就是将 bias 项初始化为 。也可以写在损失函数中：
import numpy as np
import keras.backend as K
def categorical_crossentropy_with_prior(y_true, y_pred, tau=1.0):
"""带先验分布的交叉熵
注：y_pred不用加softmax
"""
prior = xxxxxx # 自己定义好prior，shape为[num_classes]
log_prior = K.constant(np.log(prior + 1e-8))
for _ in range(K.ndim(y_pred) - 1):
log_prior = K.expand_dims(log_prior, 0)
y_pred = y_pred + tau * log_prior
return K.categorical_crossentropy(y_true, y_pred, from_logits=True)
def sparse_categorical_crossentropy_with_prior(y_true, y_pred, tau=1.0):
"""带先验分布的稀疏交叉熵
注：y_pred不用加softmax
"""
prior = xxxxxx # 自己定义好prior，shape为[num_classes]
log_prior = K.constant(np.log(prior + 1e-8))
for _ in range(K.ndim(y_pred) - 1):
log_prior = K.expand_dims(log_prior, 0)
y_pred = y_pred + tau * log_prior
return K.sparse_categorical_crossentropy(y_true, y_pred, from_logits=True)
结果分析
很明显 logit adjustment loss 也属于调整 loss 方案之一，不同的是它是在 里边调整权重，而常规的思路则是在 外调整。至于它的好处，就是互信息的好处：互信息揭示了真正重要的关联，所以给 logits 补上先验分布的 bias，能让模型做到“能靠先验解决的就靠先验解决，先验解决不了的本质部分才由模型解决”。
在预测阶段，根据不同的评测指标，我们可以制定不同的预测方案。从《函数光滑化杂谈：不可导函数的可导逼近》[4] 可以知道，对于整体准确率而言，我们有近似：
其中 是验证集。所以如果不考虑类别不均衡情况，追求更高的整体准确率，那么对于每个 x 我们直接输出 最大的类别即可。但如果我们希望每个类的准确率都尽可能高，那么我们将上式改写成：
其中 ，也标签为 y 的 x 的集合，等号右边事实上就是先将同一个 y 的项合并起来。我们知道“整体准确率=每一类的准确率的加权平均”，而上式正好具有同样的形式，所以括号里边的 就是“每一类的准确率”的一个近似了。
因此，如果我们希望每一类的准确率都尽可能高，我们则要输出使得 最大的类别（不加权）。结合 的形式，我们有结论：
第一种其实就是输出条件概率最大者，而第二种就是输出互信息最大者，按具体需求选择。
至于详细的实验结果，大家可以自行看论文，总之就是好到有点意外：
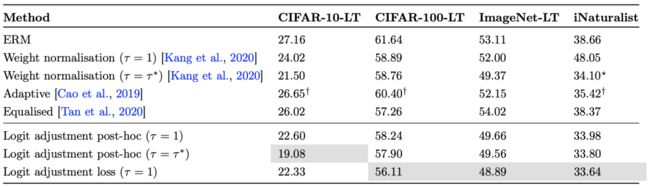▲ 原论文的实验结果
文末小结
本文简单介绍了一种基于互信息思想的类别不平衡处理办法，该方案以前笔者也曾经构思过，不过没有深究，而最近 Google 的一篇论文也给出了同样的方法，遂在此简单记录分析一下，最后 Google 给出的实验结果显示该方法能达到 SOTA 的水平。
参考文献
[1] https://arxiv.org/abs/2007.07314
[2] https://zhuanlan.zhihu.com/p/158638078
[3] https://kexue.fm/archives/4669
[4] https://kexue.fm/archives/6620
更多阅读
#投 稿 通 道#
让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。
总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。
???? 来稿标准：
• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向）
• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志
???? 投稿邮箱：
• 投稿邮箱：[email protected]
• 所有文章配图，请单独在附件中发送
• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通
????
现在，在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。
