数据结构与算法之第五章查找知识总结笔记
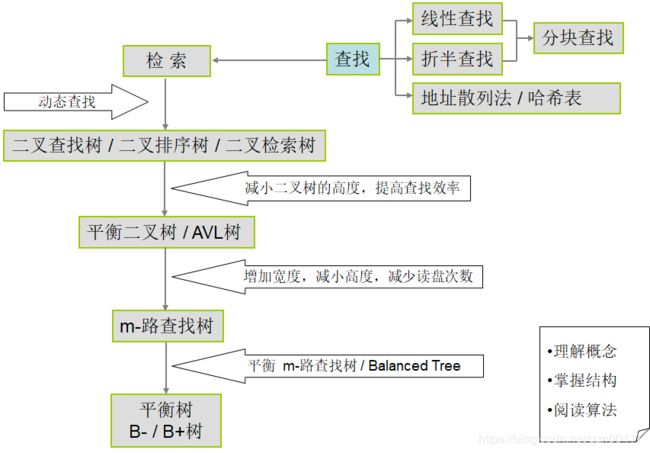
第五章：查找
5.1 线性查找
- 查找表：由同一类型的数据元素构成的集合；
- 关键字：数据元素中某一数据项的值，用以表示一个数据元素；
- 静态查找：查找+提取数据元素属性信息；
- 动态查找：查找 +（插入或删除元素）。
算法代码
//线性表
for (i=0; i<n; i++){
if (元素i == 查找目标)
查到，退出;
}
//链表
p = No.1元素
while (p != NULL){ //为空则搜索完成
if (p == 查找目标)
查到，退出;
else
p = p->next;//下一个元素
}
性能分析
- 设：Pi为查找表中第i个记录的概率，∑Pi=1；Ci为比较次数
- Pi = 1/n
- Ci = i
- 平均查找长度ASL = (1+2+···+n) * (1/n) = (1+n) / 2
5.2 折半查找
- 思想来源：
- 一定范围内，前者想一个数，后者猜
- 并让前者告诉后者“后者猜的数，比想的数大，还是小？”
- 有序数组内，数字不一定连续
- 程序作为“后者”，猜的不是“具体数字”，猜的是“索引”，即“下标”
- 有序数组，下标和数值均单调
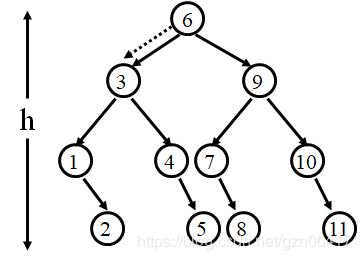
- 查找的点的前后关系
- 最多查找h次
算法代码
// 非递归
Int Binary-Search(keytype k, LIST F )
{
int low , up , mid ;
low = 1 ; up = last ; // 设置查找范围
while ( low <= up ){
mid = ( low + up ) / 2 ; // 查找中间值 ≈ 中位数
if ( F[mid].key = = k ) // 中间值即为查找的目标值
return mid ; // 返回中间值“下标”
else if ( F[mid].key > k ) // 中间值大于查找的目标值
up = mid – 1 ; // 左半边查找，且不包含中间值
else // 否则，中间值小于查找的目标值
low = mid + 1 ; // 右半边查找，且不包含中间值
}
return –1; // 返回未找到
}
// 递归
int Bsearch( F , i , j , k )
{
int m;
if (i > j) return -1 ; // 左边界大于右边界，查找范围为空，则查找完毕
else {
m=( i + j ) / 2 ; // 取中间值
if( F[m].key = = k ) // 中间值即为查找的目标值
return m; // 返回中间值“下标”
if( F[m].key < k ) // 中间值小于查找的目标值
return( Bsearch( F , i , m-1 , k) ); // 右半边查找，且不包含中间值
else // 中间值大于查找的目标值
return( Bsearch( F , m+1 , j , k) ); // 左半边查找，且不包含中间值
}
}
性能分析
- 最大查找长度 = log2(n)
- 平衡树平均查找长度 < log2(n) < (1+n)/2 = 线性查找平均查找长度
5.3 分块查找
索引表 | 22 | 44 | 74 |
数组 | 22 12 13 9 8 | 33 42 44 38 24 | 48 60 58 74 47 |
算法步骤
- 通过索引表线性查找确定在数组的哪一“块”
- 通过数组里所在“块”的线性查找确定是否存在、在哪个位置
算法代码
Keytype k; // 关键字
int blocks; // 整个索引表的长度
int last; // 整个数组的长度 last = blocks * L
index ix LIST F ;
int L ;
Int index_search( k, last, blocks, ix, F,L )
{
int i, j ; // i是索引表坐标，j是数组每块的坐标
i = 0; // 第一位索引表
while (( ix[i] < k) && (i < blocks) ) i++ ;
// 当前查找值小于目标值 且 查找的坐标在索引表范围内
if ( i < blocks ) { // i在范围内则说明上一行代码有查找到，不在范围内则没查找到
j = i*L; // 每块长度为L，要在第i块内查找，数组内的坐标j为i×L
while (( k != F[j].key ) && (j <= (i+1)*L-1 ) && (j < last))
// 当前查找值目标值不同 且 坐标j在范围内 且 j在整个数组范围内（防止查找最后一“块”时越界）
j = j + 1; // 查找块内的下一个查找元素
if ( k == F[ j ].key ) return j ; // 若查找到则返回下标
/* 执行这条语句，有可能是：
1. 上一个while的第一个条件不满足（即查找成功！）
2. 第二/三个条件不满足（即越界≈无目标值，查找失败
*/
}
return –1 ; // 查找失败
}
5.4 二叉查找树
- 特点
- 左子树所有值都小于根值
- 右子树所有值都大于根值
- 理论上不能有相同
- 操作
- 查找
- 插入
- 删除
查找
- 判断与根值是否相等，相等则完成
- 否则，判断与根值大小关系
- 若小于根值，则：当目标值存在时，值一定左子树里
- 若大于根值，则：当目标值存在时，值一定右子树里
- 当搜索到空时，则不存在
BST search( keytype k, BST F ) // k：目标值；F：当前查找子树的根节点
{
p = F ;
if ( p == NULL ) return Null ;
else if (k == p->data.key) return p; // 相等，查找成功
else if (k < p->data.key) // 目标值小于根值
return search (k, p->lchild); // 进入左子树
else if (k > p->data.key) // 目标值大于根值
return search (k, p->rchild); // 进入右子树
}
插入
- 核心点：值一定在树的最底端插入
- 因此，从根节点往下搜索合适的插入位置时，一定要到一个***“空位”（NULL）才能新建节点***
- 依据性质：左子树的所有值一定小于根值，右子树的所有值一定小于根值
- 在任意一个时刻，小于根值则插入左子树，大于根值则插入右子树
- 当选择的子树为空时则插入（新建节点）
- 程序中的这一步：先假设不为空，进入这一节点（NULL），再在进入迭代时
Void Insert (Records R, BST &F)
{
if ( F == NULL ) { // 已经查找到底层，可以插入新节点
F = new CellType ; // 新建节点
F->data = R ; // 存值
F->lchild = NULL ; // 预设左右子树都为NULL
F->rchild = NULL ;
}
else if ( R.key < F->data.key ) // 插入的值小于根值，往左子树插入
Insert ( R , F->lchild )
else if ( R.key >= F->data.key ) // 插入的值大于根值，往右子树插入
Insert ( R , F->rchild )
}
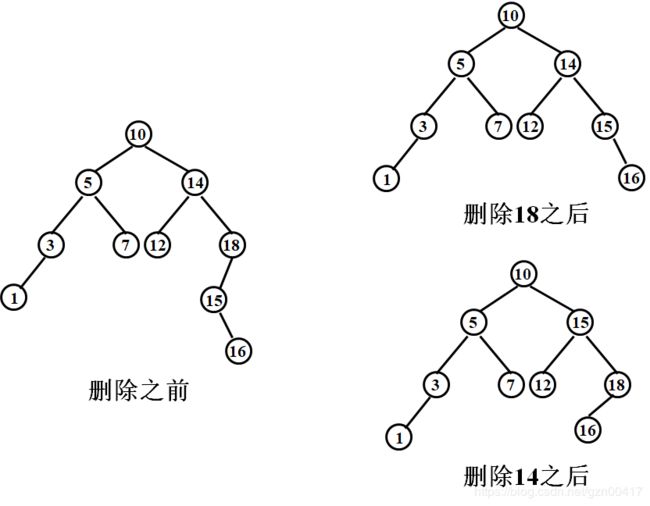
删除
删除三类结点：
- 被删除的结点是叶子结点
- 被删除的结点只有一颗非空的左子树或右子树
- 被删除的结点有两棵非空的子树
Void Delete ( keytype k ,BST &F )
{
if ( F != NULL )
if ( k < F->data.key ) Delete( k, f->lchild ) ; // 目标值比根值小，进入左儿子
else if ( k > F->data.key ) Delete( k, f->rchild ); // 目标值比根值大，进入右儿子
else // 找到该元素，开始删除
if ( F->rchild == NULL ) F = F->lchild ; // 一边儿子为空，则用另一边儿子代替
else if ( F->lchild == NULL ) F = F->rchild ;
else F->data = DeleteMin(F->rchild) // 两边都有儿子，进行DeleteMin操作
}
// 取右子树中最小的（即最左儿子），DeleteMin以此为例
// 同理，也可以取左子树最大
Records DeleteMin( F ) // F：右子树的根
{
records tmp ;
BST p ;
if ( F->lchild == NULL ) { // 已经找到最左儿子
p = F ;
tmp = F->data ; // 暂存节点的信息
F = F->rchild ; // 该节点删除，右儿子补上（无左儿子 and 可能是空）
Delete p ; // 删除p（当前F）节点
return tmp ; // 返回data给上个函数要删除的点，即将右子树的最左儿子的移到删除点的位置
}
else
return ( DeleteMin( F->lchild ) ; // 未找到最左，继续往左找
}
5.5 平衡二叉树/AVL树
定义
- 平衡树是具有如下性质的二叉查找树：其左子树和右子树都是高度平衡的二叉树，且左子树和右子树高度之差的绝对值不超过1。
- 结点的平衡因子 BF (Balanced Factor) 定义为：结点左子树与右子树的高度之差。
- 平衡树中的任意结点的 BF 只可能是 -1，0，+1
- 例题：下述二叉树中,哪一种满足性质:从任一结点出发到根的路径上所经过的结点序列按其关键字有序。
- Choices：(A) 二叉排序树 (B) AVL树 © 堆
- 分析：
- 选项A：根据二叉排序树的结构特点我们可以知道，二叉排序树的中序遍历结果是一个有序序列，而在中序遍历中，父结点并不总是出现在孩子结点的前面（或后面），故该选项不正确。
- 选项B：AVL树其本质上也是一种二叉排序树，只不过是平衡化之后的二叉排序树，故该选项也是不正确的。
- 选项C：根据建堆的过程，不断地把大者“上浮”，将小者“筛选”下去，最终得到的正是一个从任一结点出发到根的路径上所经过的结点序列按其关键字有序的树状结构。
插入
-
每次插入时，发现有任意一点平衡因子不是-1，0，+1，则进行旋转操作
-
主要涉及2点的旋转
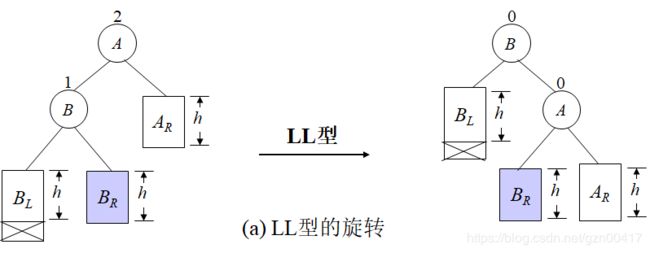
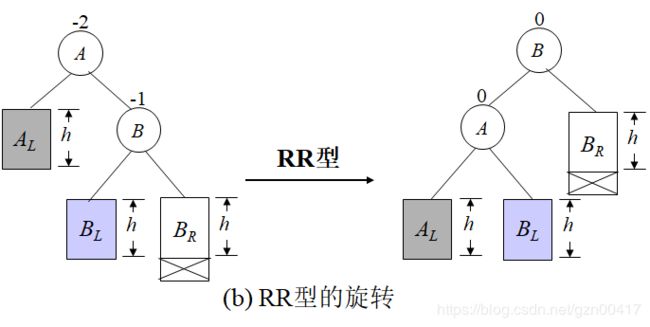
- LL：新结点Y被插入到A的左子树的左子树上；
- RR：新结点Y被插入到A的右子树的右子树上；
-
主要涉及3点的旋转
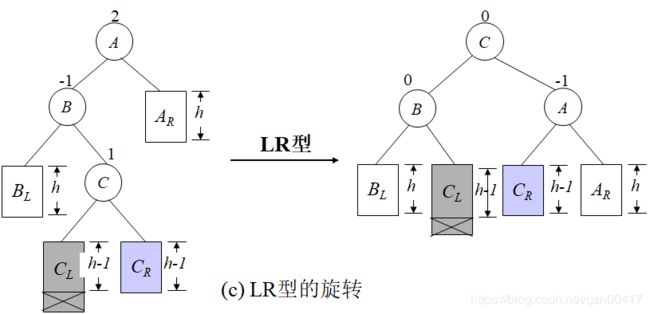
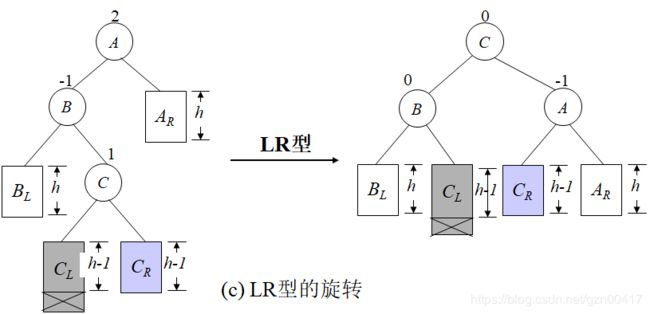
- LR：新结点Y被插入到A的左子树的右子树上；
- RL：新结点Y被插入到A的右子树的左子树上；
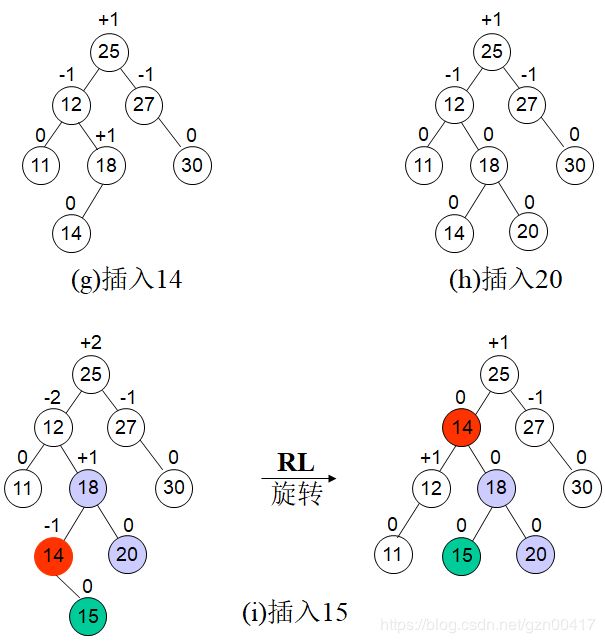
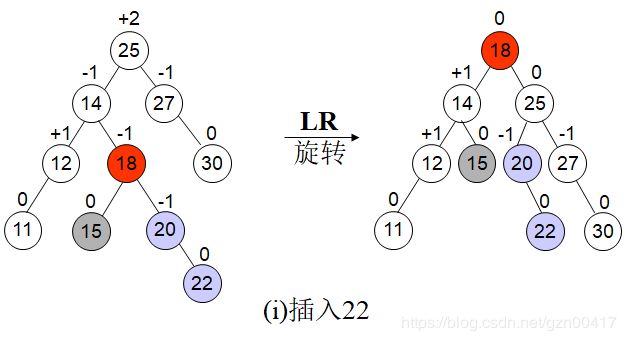
LL & RR
LR && RL
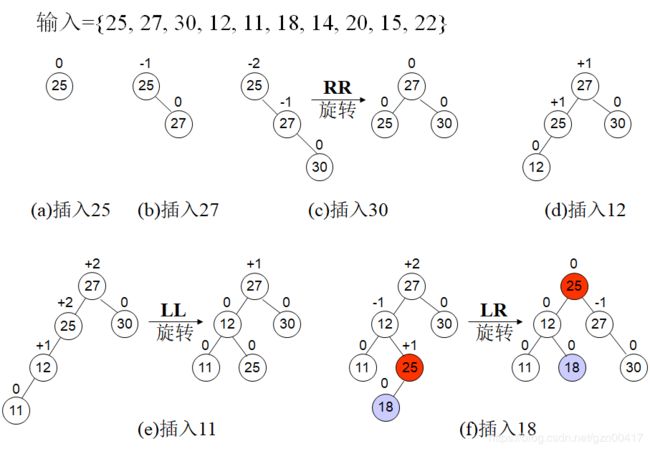
例题演示
查找
- 方法与二叉查找树相同
- 平均查找长度
- 相同节点时，期望相同
- 平衡树方差小
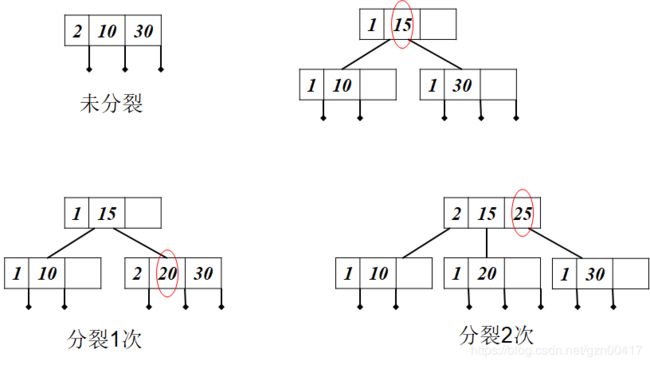
5.6 B-树
概念
B-树（Balanced-Tree）：B-树是一种非二叉的查找树
除了要满足查找树的特性，还要满足以下结构特性。一棵 m 阶的 B- 树：
（1）树的根或者是一片叶子(一个节点的树),或者其儿子数在 2 和 m 之间；
（2）除根外，所有的非叶子结点的孩子数在 m/2 和 m 之间；
（3）所有的叶子结点都在相同的深度。
查找
B-树上的查找有两个基本步骤：
- 在B-树中查找结点，该查找涉及读盘操作，属外部查找；
- 在结点内查找，该查找属内查找；
查找操作的时间为：
- 外查找的读盘次数不超过树高h，故其时间是O(h)；
- 内查找中，每个结点内的关键字数目keynum
插入
删除
- 待更新
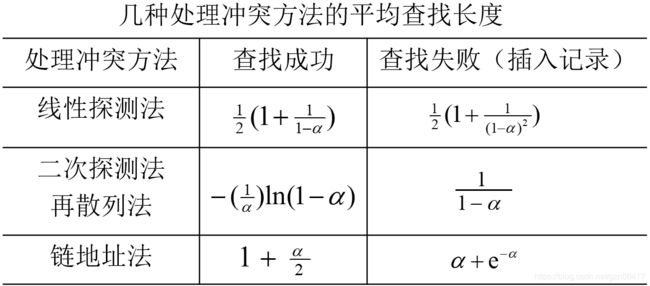
5.7 地址散列法（哈希查找）
关键问题：
- 构造Hash函数
- 制订解决冲突的方法
- 装载因子α = 表中装入的记录数 / 哈希表的长度
装填因子α标志着哈希表的装满程度，α越小，发生冲突的可能性越小，反之，发生冲突的可能性越大。- 成功查找平均查找长度ASLs：查找到散列表中已存在结点的平均比较次数。
失败查找平均查找长度ASLu：查找失败，但找到插入位置的平均比较次数。
构造散列函数
-
散列函数分类：
- 内散列表（数组）
- 外散列表（链表）
-
构造方法：
- 直接定址法
- Hash( key ) = key ; 或 Hash( key ) = a·key+b ;
- 质数除余法
- 设桶数B，取质数 m ≤ B
- Hash ( key ) = key % m
- 平方取中法
- 取 key 2 的中间的几位数作为散列地址
- 折叠法
- 数字分析法
- 如图所示，假设散列表长为10010，可取中间4位中的两位为散例地址。
- 随机数法
- 直接定址法
-
构造Hash函数应注意以下几个问题：
- 计算Hash函数所需时间；
- 关键字的长度；
- 散列表的大小；
- 关键字的分布情况；
- 记录的查找频率；
解决冲突
-
开放定址法
- Hi = ( H(key) + di ) MOD m i = 1,2,…,k ( k≤m-2 )
- H(key) 为哈希函数，m为表长，d i 为增量序列：
(1) di = 1,2,3,…,m-1
(2) di = 12,-12,2^2,-22,…,± k^2 (k ≤m/2)
(3) di 为伪随机序列，称为伪随机探测再散列
-
再散列法
- Hi = Rhi (key) i=1,2,…,k
-
链地址法
-
建立一个公共溢出区
内容总结
具体内容请返回上述总结和书本中查看
- A：基本概念
查找（检索） 查找表 关键字 静态查找 动态查找 平均查找长度 - B：线性查找
- C：折半查找：条件
- D：分快查找
- E：AVL树
- F：B-树B+树
- G：二叉查找树：什么叫二叉查找树、插入结点、删除结点、查找结点
- H：散列法：哈希函数 冲突 哈希表的长度
- 哈希函数：直接定址法 质数除余法 平方取中法
折叠法 数字分析法 随机法 - 处理冲突：开放定址法（线性探测、二次探测）
再散列法 链地址法 建立公共溢出区
- 哈希函数：直接定址法 质数除余法 平方取中法
- I：装载因子
- J：成功查找平均查找长度
- K：失败查找平均查找长度
