干货--C5.0与CART算法实战
在上一期的《浅谈C5.0与CART算法的比较--理论理解》我们详细讲解了有关C5.0决策树和CART决策树的理论知识,包括构造树过程中如何选择节点变量、节点变量的分割点、如何完成剪枝,避免模型的过拟合,从而增强树模型的泛化能力。接下来我们将从实际的案例中来比较两个算法的实现,希望读者在阅读本文时能够再次查看上面提到的那篇理论理解,这将有助于解读后文的落地。
本文实战部分的数据来自于UCI机器学习网站(http://archive.ics.uci.edu/ml/),后文会给出脚本及数据下载的链接。该数据的因变量是反映某银行顾客是否会缴纳一项保证金,总共有45211条记录和16个自变量。各个自变量的含义如下:
age:年龄;
job:工作类型(如行政、管理者、失业等);
marital:婚姻状态(已婚、未婚、离异);
education:教育程度(初等教育、中等教育、高等教育);
default:是否拥有信用卡;
balance:平均年余额;
housing:是否有房贷;
loan:是否有个人贷款;
contact:联系方式(固定电话、手机);
day:最后一次联系的日;
month;最后一次联系的月;
duration;最后一次联系的时长(秒为单位);
campaign:在本次市场活动中联系的次数;
pdays:最后一次联系的时间距离上一次市场活动的间隔天数(-1表示该用户在上一次活动中没有联系);
previous:上一次活动中,联系的次数;
poutcome:上一次市场活动的结果(成功、失败、其他);
接下来我们就利用上面所说的数据集进行建模:
# 加载所需的第三方包
if(!suppressWarnings(require('Hmisc'))){
install.packages('Hmisc')
require('Hmisc')
}
if(!suppressWarnings(require('C50'))){
install.packages('C50')
require('C50')
}
if(!suppressWarnings(require('rpart'))){
install.packages('rpart')
require('rpart')
}
# 读取数据集
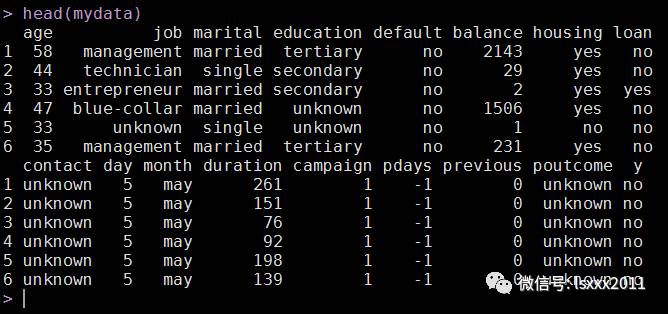
mydata <- read.csv(file = file.choose(), sep = ';')
head(mydata)
# 筛选出因子型变量,并对这些变量作统计
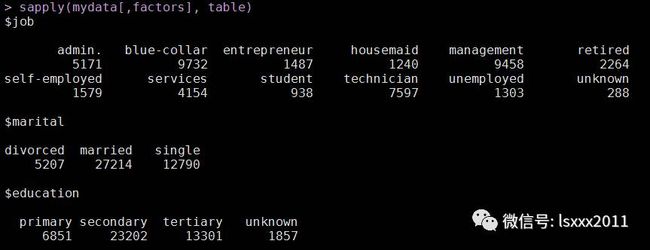
factors <- names(mydata)[sapply(mydata,class) == 'factor']
sapply(mydata[,factors], table)
上图为截取的一部分。
# 数据清洗
# 将job中未知职业的记录删除(仅占0.64%),并删除缺失严重的变量poutcome(占82%)。
clear.mydata <- subset(mydata, job != 'unknown',
select = -poutcome)
dim(mydata)
dim(clear.mydata)
# 受教育程度中有1857个未知,我们不妨用众数(secondary)替补
education.impute <- ifelse(clear.mydata$education != 'unknown',
as.character(clear.mydata$education),
'secondary')
# 至少有28%的观测在contact变量上是缺失的,不妨我们按工作种类分组填补。
# 首先将unknown设置为R中的缺失标志NA
clear.mydata$contact <- as.character(clear.mydata$contact)
table(clear.mydata$contact)
clear.mydata$contact[clear.mydata$contact == 'unknown'] <- NA
table(clear.mydata$contact, useNA = 'ifany')
由于R中没有自带的众数函数,这里我们自定义一个众数函数。
# 自定义众数函数
stat.mode <- function(x, rm.na = TRUE){
if (rm.na == TRUE){
y = x[!is.na(x)]
}
res = names(table(y))[which.max(table(y))]
return(res)
}
# 自定义函数,实现分组替补
my.impute <- function(data, category.col = NULL,
miss.col = NULL, method = stat.mode){
impute.data = NULL
for(i in as.character(unique(data[,category.col]))){
sub.data = subset(data, data[,category.col] == i)
sub.data[,miss.col] = impute(sub.data[,miss.col], method)
impute.data = c(impute.data, sub.data[,miss.col])
}
data[,miss.col] = impute.data
return(data)
}
其中,category.col 指定所要分组的变量,miss.col指定需要填补的缺失值变量,默认的方法为众数填补。
clear.mydata <- my.impute(clear.mydata, category.col = 'job',
miss.col = 'contact')
table(clear.mydata$contact, useNA = 'ifany')
很显然,那些缺失的观测全被替补成了"cellular"沟通方式,说明在各组中联系方式的众数为"cellular"。
# 再将字符串变量转换为因子型变量
clear.mydata$contact <- factor(clear.mydata$contact)
# 数据合并
final.data <- cbind(clear.mydata,education.impute)
final.data <- final.data[,-4]
# 简单的了解一下数据
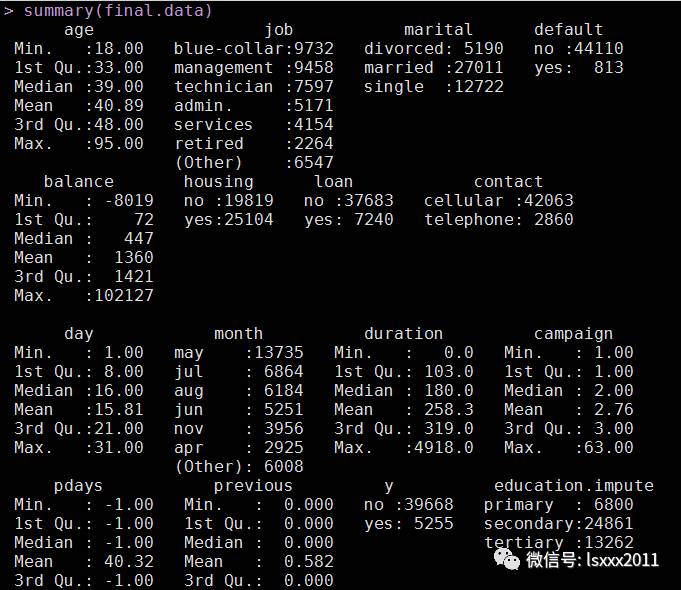
str(final.data)
summary(final.data)
上面的过程全都是数据预处理的过程,接下来我们要对处理好的数据进行建模和预测:
# 抽样,并将总体分为训练集和测试集
set.seed(1)
index <- sample(1:nrow(final.data), size = 0.75*nrow(final.data))
train <- final.data[index,]
test <- final.data[-index,]
# 大致查看抽样与总体之间是否吻合
prop.table(table(final.data$y))
prop.table(table(train$y))
prop.table(table(test$y))
# 构建C5.0决策树,并对重要变量进行筛选
fit <- C5.0(x = train[,-15], y = train[,15],
control = C5.0Control(winnow = TRUE))
summary(fit)
从结果中看,模型选择的重要变量为duration,housing,month,campaign,previous,day,pdays,marital,loan,age,接下来我们就利用这些变量,多模型进行修正。
# 建模并预测
vars <- c('y','duration','housing','month',
'campaign','previous','day','pdays',
'marital','loan','age')
train2 <- train[,vars]
test2 <- test[,vars]
# 建模
fit1 <- C5.0(x = train2[,-1], y = train2[,1])
# 预测
pred1 <- predict(fit1, newdata = test2[,-1])
# 混淆矩阵
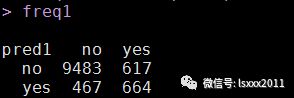
freq1 <- table(pred1, test2[,1])
freq1
# 准确率
accuracy1 <- sum(diag(freq1))/sum(freq1)
accuracy1
# 正例的覆盖率
recall1 <- freq1[2,2]/sum(freq1[,2])
recall1
虽然模型的准确率达到90%以上,但预测正确的yes在实际的yes中只占了51.8%,即正例的覆盖率并不高,模型的准确性值得怀疑。
C5.0算法可通过错误率和损失矩阵进行剪枝,之前的文章提过,默认的alpha(置信水平)为0.25,当alpha设置低于0.25时,将会进行剪枝。为了确定最佳的alpha值,我们自定一个函数,通过遍历的方式确定alpha。
# 剪枝--基于错误率的剪枝法
err.rate <- function(train, test, y.index = NULL, y.name = NULL){
alpha <- NULL
res <- NULL
if(is.null(y.index)){
y.index = which(names(train) == y.name)
}
for (i in seq(0.25,0.1,-0.01)){
fit <- C5.0(x = train[,-y.index], y = train[,y.index],
control = C5.0Control(CF = i))
pred <- predict(fit, newdata = test[,-y.index])
freq <- table(pred, test[,y.index])
accuracy <- sum(diag(freq))/sum(freq)
alpha <- c(alpha,i)
res <- c(res,accuracy)
}
return(data.frame(alpha,res))
}
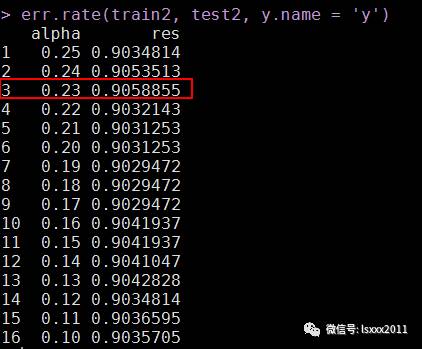
err.rate(train2, test2, y.name = 'y')
根据上面的结果,我们确定alpha值为0.23,此时模型的准确率提高了一点点,于是我们基于这个值,再结合损失矩阵再做一次模型的构建和预测。
# 构建损失矩阵(注意必须为矩阵设置行名称和列名称)
costs <- matrix(c(0,4,1,0), ncol = 2, byrow = TRUE,
dimnames = list(unique(train2$y),unique(train2$y)))
# 同过control参数设置alpha值
fit3 <- C5.0(x = train2[,-1], y = train2[,1],
control = C5.0Control(CF = 0.23),
costs = costs)
# 预测
pred3 <- predict(fit3, newdata = test2[,-1])
freq3 <- table(pred3, test2[,1])
freq3
accuracy3 <- sum(diag(freq3))/sum(freq3)
accuracy3
recall3 <- freq3[2,2]/sum(freq3[,2])
recall3
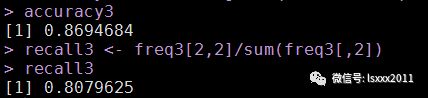
模型经过改善后,大大提高了正例的覆盖率,从原来的51.8%提升到目前的80.8%,虽然模型的整体准确率降低了3.4个百分点,但这样的损失在一定程度上是有助于业务市场的活动,因为能够预测到更多的yes对象,就可以对这些群体进行营销,改善业务。
接下来我们再试试CART算法在该数据集上应用:
# 构建CART算法
fit4 <- rpart(y ~ ., data = train2)
# 预测
pred4 <- predict(fit4, newdata = test2[,-1], type = 'class')
# 构建混淆矩阵
freq4 <- table(pred4, test2[,1])
freq4
# 模型准确率
accuracy4 <- sum(diag(freq4))/sum(freq4)
accuracy4
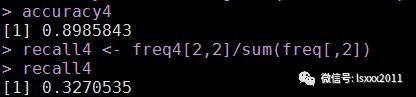
发现模型的准确率也挺高的,也在90%,但夸张的是正例的覆盖率只有32.7%,比C5.0模型什么都不做还差很多,这就需要我们对CART算法进行剪枝操作。
首先来看一下模型的cp表,可以通过cp值进行“最小代价复杂度”剪枝:
从结果中看,cp值为0.01时,误差率最低,切xerror+xstd也是达到最小,而模型构造的时候默认就是cp=0.01,故暂不需要通过cp值进行剪枝。那看看是否可以通过损失矩阵进一步优化模型:
# 剪枝--基于损失矩阵
costs <- matrix(c(0,1.25,1,0), ncol = 2, byrow = TRUE)
fit5 <- rpart(y ~ ., data = train2,
parms = list(loss = costs))
fit5
# 预测
pred5 <- predict(fit5, newdata = test2[,-1], type = 'class')
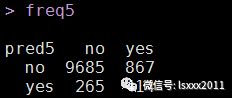
freq5 <- table(pred5, test2[,1])
freq5
accuracy5 <- sum(diag(freq5))/sum(freq5)
accuracy5
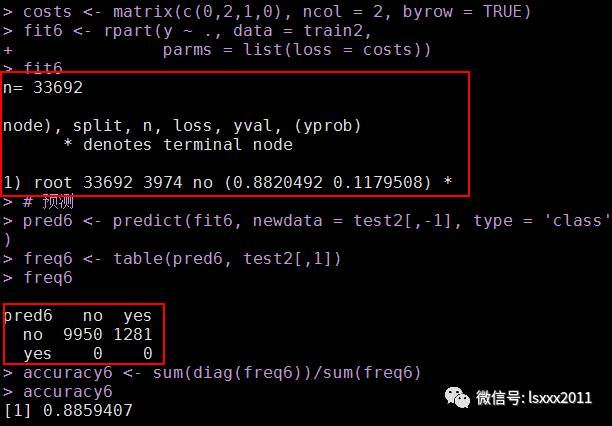
经过不停的尝试,模型效果一直不够满意,如果损失矩阵设置的大一点就会大失所望。。。如下方所示:
决策树就剩下根节点了,并没有进行树的构造。我怀疑该数据集并不适合使用CART算法进行树的构造。如果有其他观点的欢迎朋友们联系我。
OK,我们这期的实战部分就到这里。欢迎大家多多沟通和交流,通过互相学习,达到取长补短的效果。快要过年了,提前祝福各位网友和朋友2017年新年快乐,心想事成,万事如意!
数据集合脚本链接:
链接:http://pan.baidu.com/s/1ge98tG3 密码:was9
每天进步一点点2015
学习与分享,取长补短,关注小号!
![]()
长按识别二维码 马上关注