Pixhawk原生固件PX4之位姿控制算法解读

欢迎交流~ 个人 Gitter 交流平台，点击直达：

---

参考文献：Minimum Snap Trajectory Generation and Control for Quadrotors

PX4中多旋翼无人机的控制分为姿态控制和位置控制两个部分。

大致解读如下

姿态控制 mc_att_control

角度控制（外环 P）

/**
 * Attitude controller.
 * 姿态角控制    外环 P
 * Input: 'vehicle_attitude_setpoint' topics (depending on mode)
 * 输入: 姿态设定值'vehicle_attitude_setpoint'
 * Output: '_rates_sp' vector, '_thrust_sp'
 * 输出: 角速度设定值  '_rates_sp'  油门设定值   '_thrust_sp'
 */

由于偏航轴的响应比横滚俯仰慢，这里采用的是倾转分离的解耦合进行姿态角控制：

先进行一个倾斜（对齐Z轴），然后旋转（对齐X轴），这样以保证能够将当前机体坐标系迅速地旋转到目标坐标系，通过这种方式求解旋转向量（详见《视觉SLAM十四讲》）仅适用于小角度情形；

对于旋转角度大于90度的情况( cos(z,Z)<0 )时，直接将目标姿态确定的四元数虚部（旋转瞬轴）作为现在旋转向量。

进而计算角速度设定值

_rates_sp = _params.att_p.emult(e_R);  // P控制

由于偏航响应较慢，加入前馈控制

_rates_sp(2) += _v_att_sp.yaw_sp_move_rate * yaw_w * _params.yaw_ff; // 偏航前馈

其中主要是旋转向量e_R的求取

/* try to move thrust vector shortest way, because yaw response is slower than roll/pitch */
// 以最短距离移动推力向量
math::Vector<3> R_z(R(0, 2), R(1, 2), R(2, 2));
math::Vector<3> R_sp_z(R_sp(0, 2), R_sp(1, 2), R_sp(2, 2));

/* axis and sin(angle) of desired rotation */
// 旋转向量(轴  角)
math::Vector<3> e_R = R.transposed() * (R_z % R_sp_z); // 向量叉乘即误差

/* calculate angle error */
float e_R_z_sin = e_R.length(); // R_z 和 R_sp_z皆为单位向量， |x|=1
float e_R_z_cos = R_z * R_sp_z;

/* calculate weight for yaw control */
float yaw_w = R_sp(2, 2) * R_sp(2, 2);

/* calculate rotation matrix after roll/pitch only rotation */
math::Matrix<3, 3> R_rp;

if (e_R_z_sin > 0.0f) {
    /* get axis-angle representation */
    float e_R_z_angle = atan2f(e_R_z_sin, e_R_z_cos);
    math::Vector<3> e_R_z_axis = e_R / e_R_z_sin;

    e_R = e_R_z_axis * e_R_z_angle; // 旋转向量: 长度为 theta角大小

    /* cross product matrix for e_R_axis */
    math::Matrix<3, 3> e_R_cp;
    e_R_cp.zero();
    e_R_cp(0, 1) = -e_R_z_axis(2);
    e_R_cp(0, 2) = e_R_z_axis(1);
    e_R_cp(1, 0) = e_R_z_axis(2);
    e_R_cp(1, 2) = -e_R_z_axis(0);
    e_R_cp(2, 0) = -e_R_z_axis(1);
    e_R_cp(2, 1) = e_R_z_axis(0);

    /* rotation matrix for roll/pitch only rotation */
    // 罗德里格斯公式
    // R = cos(theta) * I + (1 - cos(theta)) * n * n^T + sin(theta) * skewmatrix(n)
    R_rp = R * (_I + e_R_cp * e_R_z_sin + e_R_cp * e_R_cp * (1.0f - e_R_z_cos));

} else {
    /* zero roll/pitch rotation */
    R_rp = R;
}

////////////// 对齐X轴
/* R_rp and R_sp has the same Z axis, calculate yaw error */
math::Vector<3> R_sp_x(R_sp(0, 0), R_sp(1, 0), R_sp(2, 0));
math::Vector<3> R_rp_x(R_rp(0, 0), R_rp(1, 0), R_rp(2, 0));
e_R(2) = atan2f((R_rp_x % R_sp_x) * R_sp_z, R_rp_x * R_sp_x) * yaw_w; //tan = sin / cos

////////////////////////  大角度旋转 ///////////////////////
if (e_R_z_cos < 0.0f) {
    /* for large thrust vector rotations use another rotation method:
     * calculate angle and axis for R -> R_sp rotation directly */
     // 大的推力向量:直接计算 R->R_sp 的旋转向量(轴、角)
    math::Quaternion q_error;
    // 四元数组成为旋转轴 转过的角度  
    q_error.from_dcm(R.transposed() * R_sp);
    // 四元数实部为 cos(theta)  虚部为 u_x*sin(theta) u_y*sin  u_z*sin
    math::Vector<3> e_R_d = q_error(0) >= 0.0f ? q_error.imag()  * 2.0f : -q_error.imag() * 2.0f;

    /* use fusion of Z axis based rotation and direct rotation */
    // 使用基于Z轴的旋转和直接旋转的融合
    float direct_w = e_R_z_cos * e_R_z_cos * yaw_w;
    e_R = e_R * (1.0f - direct_w) + e_R_d * direct_w;
}

角速度控制（内环PID）

/*
 * Attitude rates controller.
 * 角速度控制环     内环 PID
 * Input: '_rates_sp' vector, '_thrust_sp'
 * 输入: 角速度设定值'_rates_sp'   推力设定值 '_thrust_sp'
 * Output: '_att_control' vector
 * 输出: 姿态控制量  '_att_control'
 */

角速度控制过程比较直观，需要注意的是一个系数tpa(Throttle PID Attenuation，油门PID衰减)。

/* throttle pid attenuation factor */
float tpa =  fmaxf(0.0f, fminf(1.0f, 1.0f - _params.tpa_slope * (fabsf(_v_rates_sp.thrust) - _params.tpa_breakpoint)));
// 衰减因子范围在 0 ~ 1 之间

在得到角速度误差后

/* angular rates error */
// 角速度误差
math::Vector<3> rates_err = _rates_sp - rates;

进行角速度PID控制(加前馈)

_att_control = _params.rate_p.emult(rates_err * tpa) + _params.rate_d.emult(_rates_prev - rates) / dt + _rates_int +
               _params.rate_ff.emult(_rates_sp);

这里有几点需要注意的：

1. 微分控制环节的误差量选取

   标准的PID微分项 D=Kd×(e(k)−e(k−1)) ，但是这里因为角度的微分就是角速度，而陀螺仪可以直接测出角速度。此处没有将微分项作为偏差的差可能是有此考虑，直接使用 D=kd×ΔGyro/t 可以增强稳定性。

   问：串级PID外环可以只用PI吗？

   答：可以，因为内环相当于外环的D。

2. TPA的作用

   TPA在此处使用是考虑到了抗积分饱和。

   当系统存在一个方向的误差时，由于积分的累加作用会使控制量一直增大，可能会使控制量达到执行器的执行阈值，如果此时误差的方向发生改变，控制量会逐渐减小，控制量也会退出饱和区，执行器也会在阈值内执行；如果此时误差方向还是没有改变，控制量会继续增大但是执行器会一直保持在阈值，此时控制量就进入了饱和区。进入饱和区越深，退出饱和区时间就会越长，在饱和区时执行器会一直在阈值位置，如果误差发生反向，执行器不会立刻有反应，控制量会慢慢减小，等执行器推出饱和区才会有反应。这样就会使控制的动态响应变差，控制性能变差。
   抗积分饱和算法
   若 u(k-1)>Umax，只累加负的误差；若u(k-1)

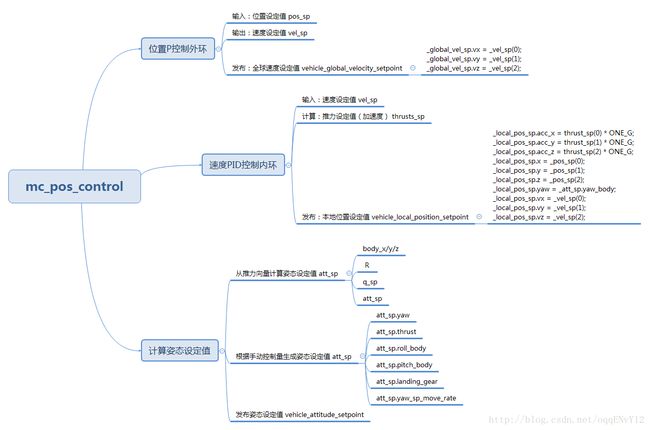
位置控制mc_pos_control

位置控制同样采用的是串级PID控制。外环为位置P控制，内环为速度PID控制。

整体控制流程入下。

保方向饱和

…

---

                                          By Fantasy