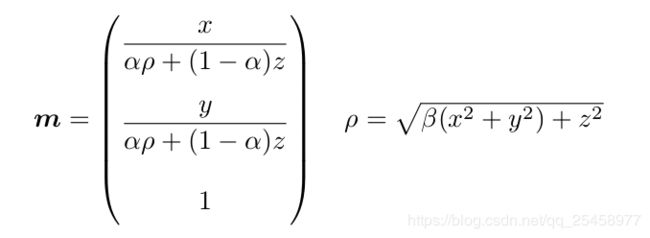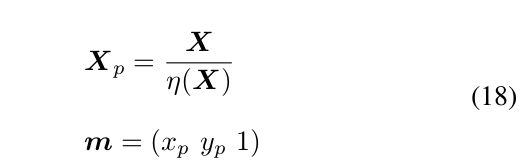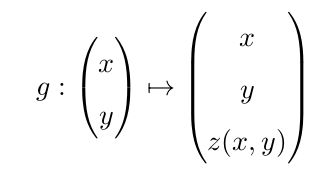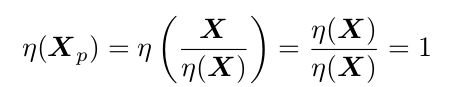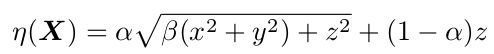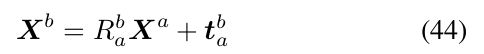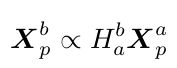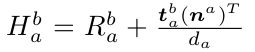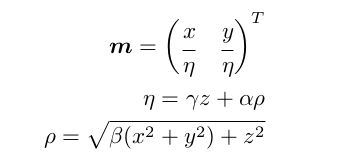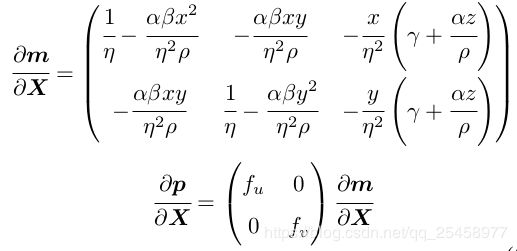EUCM鱼眼相机模型详解

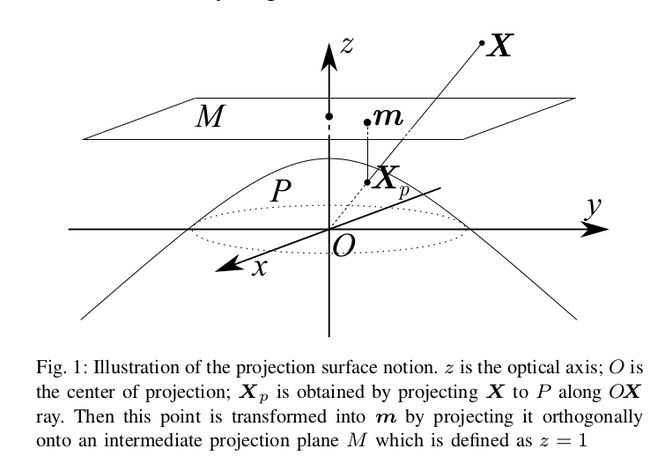
EUCM 模型即为extended unified camera model， 主要会涉及到几个坐标系，如下：
a. 世界坐标系： 真实世界坐标中的位置坐标，单位为m，　一般对应在表达为Ｘ；

b. 椭球面坐标系：是一个中转球面，与对应点的世界坐标相差一个scale的系数；也成为Ｐ平面， 对应表达为Xp

c. 图像坐标系：是椭球面上的点在z=1平面上的投影，也称为M平面，其x，y值与Xp一样，只是z值固定为1， 对应表达为m

d. 像素坐标系： 图片中点像素点坐标，左上角为(0,0)， 由 m plane中的点经过内参矩阵K计算而来；对应表达为p(u,v)

模型图像为：

1. EUCM模型的projection公式( 从世界坐标 ---> 图像坐标系)

其中( x, y, z) 为点X 在世界坐标系下的坐标；alpha， beta算作是畸变系数；得到的m 坐标即为 点X 对应的在图像坐标系下的坐标；

2. 图像坐标系到像素坐标系

3. 世界坐标系---> 椭球面坐标系( ---> M平面图像坐标系)

该公式表明 从世界坐标X 到椭球面坐标Xp 其实就是经过函数的缩放而已， 然后再由椭球面P上垂直投影到M平面上

4. 反投影 -->  这里需要注意的是， 反投影只能从像素坐标系到椭球面坐标系，而不能转换到真实的世界坐标系；

其中 x,y M 平面的坐标， 同时，也是Xp的x, y坐标， 所以重点是这里z(x,y)的求解；

式37 是z的求解公式， 这里需要注意的是若想要z值有效， 则r2 必须满足式39， 这个其实就是鱼眼相机的有效成像半径；其中gamma = 1-alpha；

5. Z(x,y)的求解方法

在第三部分中z的求解方法其实是基于P平面上的点Xp 经过缩放函数后等于1， 即：

假设Xp(x, y,z) 则 带入到第三部分的公式后有：

对该公式求解即可得到式37 ；

6.  单应矩阵求解 , 求解单应矩阵进行3D reconstruction

假设有相机a 和 b，世界坐标中某点在相机a 和 b 下分别有 坐标和

 以及有 projection functions和 ， 两个相机之间有R t 关系如下：

则推导可得：

其中，

H为3x3矩阵， 可以由 4对处在P平面的匹配点计算得出

7. 雅克比矩阵：

首先说雅克比矩阵， 在slam14讲中有关于雅克比矩阵在BA优化时的公式， p164， 式7.41

e 关于扰动量的导数， 等于e关于P‘ 的导数 × P’ 关于扰动的导数；

因为第二项是固定的，P‘ 为世界坐标[X', Y',Z'], 所以只需要注意e关于P’ 求导即可；

其中e为从世界坐标系到图像坐标系的转换公式， 对于针孔相机模型而言， 为

u = fx*X'/Z' +cx, v=fy*Y'/Z' +cy ;

对EUCM模型为

u=mx*fx + cx  , v=my*fx + cy ;

其中，

先求出m关P(x, y, z) 的导数， 再相乘， 最后结果为