gurobi+Python的实例使用(简单整数规划)
gurobi是由美国Gurobi公司开发的新一代大规模数学规划优化器,在 Decision Tree for Optimization Software 网站举行的第三方优化器评估中,展示出更快的优化速度和精度,成为优化器领域的新翘楚。
通过一个简单的整数规划实例,感受一下gurobi的魅力。
题目图片中缺少一个约束条件——每部电影至少放映一次。
from gurobipy import *
# 8部电影
# 7个影厅
# 8个时段
lt_seat = [118, 86, 116, 85, 156, 142, 156]
# 一行为一个影厅,一列为一部电影
lt_price = [[60, 60, 65, 60, 65, 90, 60, 65],
[65, 65, 85, 75, 60, 75, 85, 80],
[60, 70, 75, 80, 75, 80, 80, 75],
[65, 65, 80, 75, 80, 75, 75, 80],
[60, 65, 65, 60, 75, 80, 80, 75],
[60, 65, 65, 80, 75, 75, 80, 75],
[60, 60, 75, 80, 75, 70, 60, 75]]
# 一行为一个时段,一列为一部电影
lt_rate = [[0.50, 0.55, 0.45, 0.50, 0.60, 0.46, 0.55, 0.45],
[0.42, 0.43, 0.41, 0.43, 0.45, 0.30, 0.53, 0.36],
[0.58, 0.63, 0.67, 0.64, 0.70, 0.64, 0.54, 0.57],
[0.62, 0.67, 0.70, 0.65, 0.75, 0.64, 0.53, 0.66],
[0.65, 0.65, 0.73, 0.68, 0.75, 0.74, 0.67, 0.72],
[0.66, 0.69, 0.78, 0.78, 0.78, 0.75, 0.74, 0.70],
[0.67, 0.92, 0.87, 0.87, 0.75, 0.59, 0.68, 0.68],
[0.67, 0.92, 0.87, 0.87, 0.75, 0.59, 0.68, 0.68]]
# 计算满座的票房二维列表,lt_all
lt_all = [[0 for col in range(8)] for row in range(7)]
for i in range(7):
for j in range(8):
lt_all[i][j] = lt_price[i][j] * lt_seat[i]
# 创建模型
m = Model("arr_mov")
# 创建变量.第i个时段在第j个影厅放映第k部电影
x = m.addVars(8, 7, 8, vtype=GRB.BINARY)
# 更新变量环境
m.update()
# 创建目标函数
m.setObjective(sum(x[i, j, k] * lt_rate[i][k] * lt_all[j][k]
for i in range(8) for j in range(7) for k in range(8)),
GRB.MAXIMIZE)
# 创建约束条件约束条件
m.addConstrs(sum(x[i,j,k] for i in range(8) for j in range(7)) >= 1 for k in range(8))
m.addConstrs(sum(x.select(i, j, '*')) == 1 for i in range(8) for j in range(7))
# 执行现行规划模型
m.optimize()
# 输出结果
result = [[0 for col in range(7)] for row in range(8)]
solution = m.getAttr('x',x)
# 得到排片矩阵
for k,v in solution.items():
if v == 1:
result[k[0]][k[1]] = k[2] + 1
# 得到最大收益值
max_get = sum(solution[i, j, k] * lt_rate[i][k] * lt_all[j][k] for i in range(8) for j in range(7) for k in range(8))
# 打印最大收益值,和排片矩阵
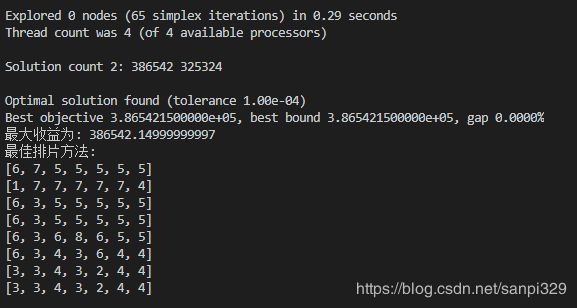
print('最大收益为:',max_get)
print('最佳排片方法:')
for l in result:
print(l)