Libra R-CNN论文解读及复现

一篇来自浙大、港中文、商汤的目标检测文章。
现在CV领域各种模型真的是满天飞，这篇Libra RCNN在不大量增加模型复杂度的前提下还可以有效涨分，还是给人眼前一亮的。
论文链接

总览

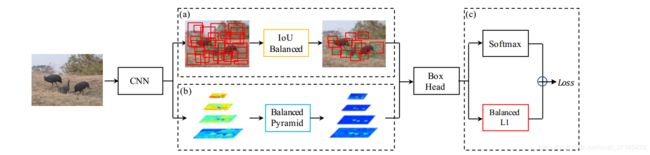
论文主要讲述了三个贡献：

• IoU-balanced sampling—— reducing the imbalance at sample，让选择的样本更 representative；
• balanced feature pyramid—— reducing the imbalance at feature，更加有效地整合利用多尺度特征；
• balanced L1 loss—— reducing the imbalance at objective，设计了一个更优的loss，引导整体训练更好的收敛；
  

1.IoU-balanced Sampling

在anchor-base的目标检测中，网络head输出大量的anchors（或者叫default boxes），这些box对于匹配到的ground truth有各自不同iou，而大部分iou都很小（负样本比例巨大），如果直接将所有正负样本送入loss的计算将会导致模型往背景的方向过拟合，因此前人做了很多解决正负样本不平衡的工作（例如在faster rcnn的RPN层中随机采样保证正负样本1：1；SSD中采用了难样本挖掘；OHEM等等），但是作者认为之前的方法多少还是有各自的缺点，比如OHEM对不干净的数据集不够鲁棒，focal loss不适合two-stage任务。

注意，难样本是训练中具有代表性的样本哦（类似于学生时代的错题回顾），那么如何在避免上述问题的情况下，让模型更关注于此呢？

作者的思路：既然选择box的方式是sampling，那么sampling的时候能不能找到一些规律呢。因此做了下面的统计：

上面统计了随机采样和难样本随iou的分布。
可以知道：超过60%的hard negative与gt超过0.05的iou；但随机采样只有30%超过0.05iou；说明困难样本并不根据iou均匀分布在原有样本中，也就是两者分布不match！既然说要让模型更关注于hard example，那怎么结合这样的规律来做点事情呢？
作者的思路：分层抽样替换随机抽样

K：将原有对负样本的采样区间分成K个区间（不一定要均匀）；
N：总共采的负样本数；
M_k：每个区间sampling candidates数量；
p_k：最终算出每个区间采样的概率。

可以看出后两个变量反相关，candidates越少，越倾向于sample，这样做，表面上是有效提高了高iou区间的样本比例，但深层原因是给了一个先验的分布，将hard example与sample的分布match起来（注意这个分布也算是hyper-parameters，跟数据集有关的）。
不过我认为，作者这样做也无法保证采的每一个样本都hard呀，但是不可否认的是，这是在不增加计算量的前提下，尽可能提高hard的比例。

代码复现

这部分是自己手撕的，对于paper里面按概率采样，我改成了在每个区间内随机采样固定box（不过这样的问题是如果区间内box candidate过少只能全部采集了），如有不对请提出宝贵建议。

'''iou balanced hard negative mining
前面代码已经定义label：i指batch，1指前景，0指背景，-1指not care
小于thresh的box label先全部设为0(back ground),需要筛去冗余box，标记为-1
'''
bg_inds = torch.nonzero(labels[i] == 0).view(-1)
intervals = cfg.HNM_INTERVAL #[0,0.05,0.1,0.5]
num_sample = cfg.HNM_NUM_SAMPLE #[96,16,16]
num_intervals = len(interval)-1 #3
for m in range(num_intervals):
    in_interval = ((max_overlaps >= intervals[m])&
                   (max_overlaps < intervals[m+1]))
    #如果区间内样本数太少则全部采样
    if torch.numel(in_interval) <= num_sample[m]:
        continue
    #如果太多则随机抽取
    else:
        rand_num = torch.from_numpy(np.random.permutation(torch.numel(in_interval))).type_as(gt_boxes).long()
        disable_inds = bg_inds[rand_num[num_sample[m]:]]
        labels[i][disable_inds] = -1 #i指batch索引 将冗余box标记定义为-1

2.Balanced Feature Pyramid

最近FPN、PANet、ZigZagNet，真是把特征融合变着花样玩，可以说特征融合是接下来的一个大趋势了。但是，上述这些方法都是top-bottom,bottom-top等方式，更多的是关注相邻分辨率，并且非相邻层所包含的语义信息在信息融合过程中会被稀释一次，所以作者认为这样的过程也是imbalance的。
思路：以FPN（faster-rcnn）为基础，对四个level的特征进行rescale，integrate和refine进一步融合特征信息，最后再和原特征相加，增强原特征。

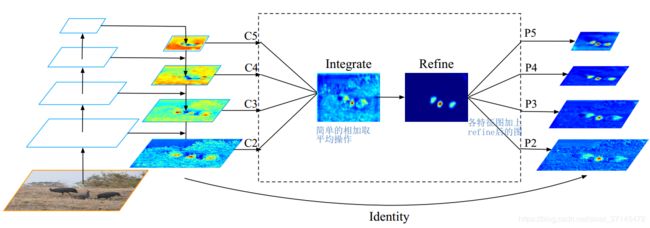
关键的refine操作使用的是kaiming大神的non-local。

non-local借鉴传统图像去噪算法，整合了全局信息，计算量少，并且输入输出维度相同，可以整合进目前各种baseline中（事实上已经有很多在这么做了），这边由于篇幅原因就不展开叙述。
而Libra RCNN利用FPN与non-local各自优势很好的解决了imbalance问题（有点像BN是不是）。

non_local复现

这部分代码参考mmdetection，代码还是非常清晰的，各位主要看一下计算过程。只截取部分代码，__ init__函数里面定义的self.g、self.theta、self.phi、self.conv_out 我都设置成了conv2d和gn组成的Sequential。

• embedded_gaussian公式：
  

def embedded_gaussian(self, theta_x, phi_x):
    #[N, HxW, C] * [N, C, HxW] ->
    # pairwise_weight: [N, HxW, HxW]
    pairwise_weight = torch.matmul(theta_x, phi_x)
    if self.use_scale:
        # theta_x.shape[-1] is `self.inter_channels`
        pairwise_weight /= theta_x.shape[-1]**-0.5
    #pairwise_weight = pairwise_weight.softmax(dim=-1)
    pairwise_weight = torch.softmax(pairwise_weight,dim=-1)
    return pairwise_weight
    
def forward(self, x):
    n, _, h, w = x.shape
    # g_x: [N, HxW, C]
    g_x = self.g(x).view(n, self.inter_channels, -1)
    g_x = g_x.permute(0, 2, 1)
    # theta_x: [N, HxW, C]
    theta_x = self.theta(x).view(n, self.inter_channels, -1)
    theta_x = theta_x.permute(0, 2, 1)
    # phi_x: [N, C, HxW]
    phi_x = self.phi(x).view(n, self.inter_channels, -1)
    # pairwise_weight: [N, HxW, HxW]
    pairwise_weight = self.embedded_gaussian(theta_x, phi_x)
    # y: [N, HxW, C]
    y = torch.matmul(pairwise_weight, g_x)
    # y: [N, C, H, W]
    y = y.permute(0, 2, 1).reshape(n, self.inter_channels, h, w)
    output = x + self.conv_out(y)
    return output

BFP复现

这边就是整合FPN中的上下文信息进行的一系列操作。就放了forward函数。

def forward(self, inputs):
	assert len(inputs) == self.num_levels
	#{C2; C3; C4; C5} channel:256
	# step 1: 整合四个特征图，resize成相同维度
	#使用了F.adaptive_max_pool2d和F.upsample，注意pytorch版本的区别，所以可能要换一下函数。
	feats = []
	gather_size = inputs[self.refine_level].size()[2:]
	for i in range(self.num_levels):
	    input_size=inputs[i].size()[2:]
	    #print('inputs:',input_size,'gather_size:',gather_size)
	    if input_size[0] >  gather_size[0]:#i < self.refine_level:
	        gathered = F.adaptive_max_pool2d(
	            inputs[i], output_size=gather_size)
	    elif input_size[0] == gather_size[0]:#i == self.refine_level:
	        gathered = inputs[i]
	    else:
	        gathered = F.upsample(inputs[i], size=gather_size, mode='bilinear') #interpolate
	    feats.append(gathered)
	
	bsf = sum(feats) / len(feats) #取平均
	
	# step 2: 进行non-local,这边self.refine就是non-local
	bsf = self.refine(bsf)
	
	# step 3: refine后的feature加回去，并resize回原尺寸
	outs = []
	for i in range(self.num_levels):
	    out_size = inputs[i].size()[2:]
	    if out_size[0] > gather_size[0]:#i < self.refine_level:
	        #residual = F.interpolate(bsf, size=out_size, mode='nearest')
	        residual = F.upsample(bsf, size=out_size, mode='bilinear')
	    elif out_size[0] == gather_size[0]:#i == self.refine_level:
	        residual = bsf
	    else:
	        residual = F.adaptive_max_pool2d(bsf, output_size=out_size)
	    outs.append(residual + inputs[i])
	
	return tuple(outs)

3.Balanced L1 Loss

目标检测实质上是多任务学习（cls®），那么如何平衡两者的权重应该是一个值得探讨的话题。通常都是人为手动调整各任务之间的权重（比如对回归loss乘以系数），但是由于回归任务unbounded的特性，直接增大回归loss常导致对outliers更加敏感（类似于噪声）。这边把样本损失大于等于 1.0 的叫做 outliers，小于的叫做 inliers。这也不是胡乱猜测，经过统计，发现outliers贡献了70%以上的梯度，而大量的inliers只有30%的贡献。作者从损失函数的角度增大了inliers贡献的梯度，从而在分类、整体定位和准确定位方面实现更加平衡的训练。具体就是将原来的smooth L1 loss 的梯度替换为：

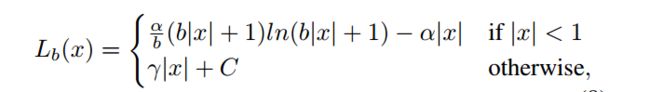
其中

γ可以调整梯度的上界，用以balance各任务所贡献的梯度。
梯度和损失函数如图：

可以看到随着α的减小，inliers的梯度能够很好地增强。

Balanced L1 Loss复现

def _balanced_l1_loss(bbox_pred, bbox_targets,alpha,gamma):
    '''bbox_pred, bbox_targets:[batch,num_boxes,4]'''
    diff=torch.abs(bbox_pred-bbox_targets)
    b = np.e**(gamma / alpha) - 1
    loss_box = torch.where(
        diff<1,
        alpha / b *(b * diff + 1) * torch.log(b * diff + 1) - alpha * diff,
        gamma * diff + gamma / b - alpha

    )
    return loss_box.mean()

其中 torch.where 用法：
第一个是判断条件，第二个是符合条件的设置值，第三个是不满足条件的设置值。

总结

三个方法都很干净，尤其是sampling和loss，即使没有改变网络结构仍然可以有效涨点。其实思路都是一样的，通过试验或统计看到潜在的imbalance现象，根据样本或loss或feature的分布来做一些事情，非常实用。