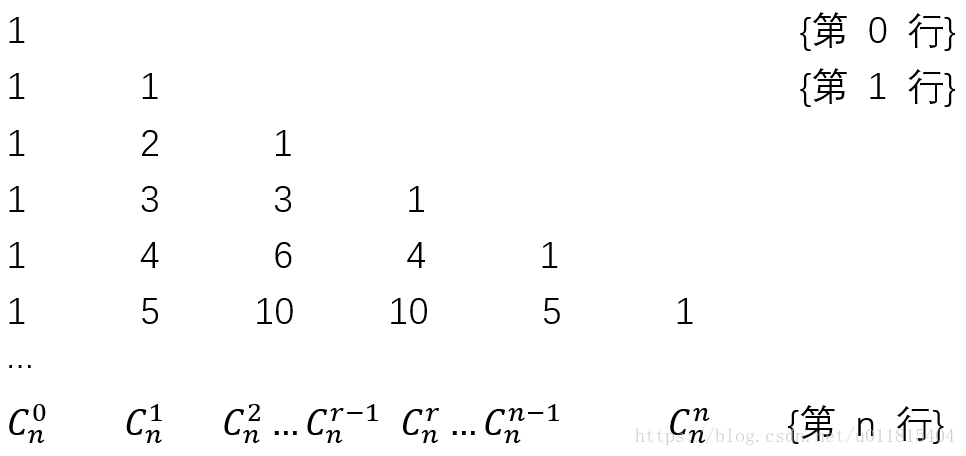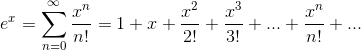组合数学 —— 母函数
【概述】
某个序列的母函数是一种形式幂级数，其每一项的系数可以提供关于这个序列的信息。
给定数列 
，构造一个函数 
，称 F(x) 为数列 的母函数，其中，序列 
只作为标志用，称为标志函数。
标志函数最重要的形式是 
，这种情况下的母函数一般形式为：
例如：
就是序列 
的母函数
也就是说，可以利用 
来讨论序列
的性质，此外还可以引入适当的函数，将问题简化，把复杂的问题变成形式上的初等代数运算。
母函数可以分成许多种，如：普通母函数、指数母函数、L 级数、贝尔级数、狄利克雷级数等等。
【普通型母函数】
1.杨辉三角
杨辉三角中第 n 行的数字就是 的展开式从低项到高项的各项系数。
而 
所以，有如下形式的杨辉三角：
将 (1+x) 与选择物品联系起来，在构造和分析一个母函数时，1 一般看成 
，用于表示没有选取一个物品，
可以看成选择了一个物品。因此 可以对应于从 n 件物品中选取了若干件物品的情况。
在一个具体的物品选择中，如果没有选择第 i 件物品，则相当于从第 i 个括号中选取了 ，如果选择了第 i 件物品，这相当于从第 i 个括号中选择了 ，这样，在 的展开式中，
前面的系数就是从 n 件物品选取了 i 件物品的所有组合情况的总数，即 
2.母函数定理
设从 n 元集合 
中取 k 个元素的组合是 
，若限定元素 
出现次数的集合为 
，则该组合数序列的母函数为：
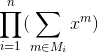
3.常见普通母函数
3.解题思路
普通母函数主要是来求组合的方案数
首先写出表达式，通常是多项的乘积，每项由多个 x^y 组成。
通用表达式为：
其中，各变量含义如下：
- k 问题中的物品种类数
- v[i] 表示该乘积表达式第 i 个因子的权重，对应于具体问题的每个物品的权重
- n1[i] 表示该乘积表达式第 i 个因子的起始系数，对应于具体问题中的每个物品的最少个数，即最少要取多少个(一般为 0)
- n2[i] 表示该乘积表达式第 i 个因子的终止系数，对应于具体问题中的每个物品的最多个数，即最多要取多少个(一般为 INF)
解题的关键是要确定 v、n1、n2 数组的值，通常情况下，n1 的值都为 0，n2 的值为无限大(INF)。
然后实现表达式相乘，从第一个因子开始乘，直到最后一个为止，此时常用一个循环来解决，每次迭代的计算结果存入数组 a[i] 中，计算结束后，a[i] 表示权重 i 的组合数，即对应具体问题的组合数。
在循环内部，将每个因子的每项与数组 a[] 中的的每项相乘，加到一个临时数组 b[] 的对应位，最后再将 b 赋给 a 即可（此处有两层循环，加上最外层循环，总共三层）。
最后的结果即为 a[P]，其中 P 为可能的最大指数。
4.例题
问题：给出 5 张 1 元，4 张 2 元，3 张 5 元的纸币，要得到 15 元，问有多少种组合？
思路：
首先可以确定 k=3，然后确定 v、n1、n2 三个数组，即：v[3]={1,2,5}，n1[3]={0,0,1}，n2[3]={5,4,3}
之后写出表达式，即：(1+x^2+x^3+x^4+x^5)(1+x^2+x^4+x^6+x^8+x^10)(x^5+x^10+x^15)，可以发现最大的可能指数 P=15
最后套用版子即可。
int a[N];//权重为i的组合数
int b[N];//临时数组
int P;//最大指数
int v[N],n1[N],n2[N];
void cal(int k){
memset(a,0,sizeof(a));
a[0]=1;
for(int i=1;i<=k;i++){//循环每个因子
memset(b,0,sizeof(b));
for(int j=n1[i];j<=n2[i]&&j*v[i]<=P;j++)//循环每个因子的每一项，若n2是无穷，则j<=n2[i]可以去掉
for(int k=0;k+j*v[i]<=P;k++)//循环a的每个项
b[k+j*v[i]]+=a[k];//把结果加到对应位
memcpy(a,b,sizeof(b));//b赋值给a
}
}
int main(){
v[1]=1; v[2]=2; v[3]=5;
n1[1]=0; n1[2]=0; n1[3]=1;
n2[1]=5; n2[2]=4; n2[3]=3;
P=15;
cal(3);
cout<5.通用模版
通常情况下，使用模版一即可，但如果数据规模比较大，就要使用模版二。
1）模版一
P 是可能的最大指数。拿上述例题来说，若要求 15 元有多少组合，那么 P 就是 15，若问最小的不能拼出的数值，那么 P 就是所有钱加起来的和。
此外，如果 n2 是无穷，那么第二层循环条件 j<=n2[i] 可以去掉。
int a[N];//权重为i的组合数,a[P]即为结果
int b[N];//临时数组
int P;//最大指数
int v[N],n1[N],n2[N];
void cal(int k){
memset(a,0,sizeof(a));
a[0]=1;
for(int i=1;i<=k;i++){//循环每个因子
memset(b,0,sizeof(b));
for(int j=n1[i];j<=n2[i]&&j*v[i]<=P;j++)//循环每个因子的每一项，若n2是无穷，则j<=n2[i]可以去掉
for(int k=0;k+j*v[i]<=P;k++)//循环a的每个项
b[k+j*v[i]]+=a[k];//把结果加到对应位
memcpy(a,b,sizeof(b));//b赋值给a
}
}2）模版二
用一个 last 变量记录目前最大的指数，这样只需要在 0..last 上进行计算，从而大大提高效率。
int a[N];//权重为i的组合数,a[P]即为结果
int b[N];//临时数组
int P;//最大指数
int v[N],n1[N],n2[N];
void cal(int k){
a[0]=1;
int last=0;
for(int i=0; i【指数型母函数】
1.定义
对于序列 
，函数 
称为序列 对应的指数母函数。
指数型母函数可以理解为：对于 
表示在一个方案中某个元素出现了 j 次，而在不同的位置中的 j 次出现是相同的，所以在排列计算总数时，只应算作一次，由排列组合的知识知道，最后的结果应该除以 
指数型母函数在使用过程中，一般会用到高等数学中的 
的泰勒展开式：
因此，指数型母函数可以简化为：
，其中，
是所需的结果。
2.应用
指数型母函数常用于求多重排列数，即：有 n 种物品，已知每种物品的数量为 
个，求从中选出 m 件物品的排列数。
对于 n 个元素，其中 
互不相同，进行全排列，可得 n! 个不同的排列。
若其中某个元素 重复了 
次，那么全排列出来的必然有重复元素，而其中真正不同的排列数应为：
，即重复度为 ni！
同理，
重复了 
次，
重复了 
次，...，
重复了 
次 
因此，对这样的 n 个元素进行全排列，可得到不同的排列个数实际上为：
若只对其中的 r 个元素进行全排列，就用到了指数型母函数：
构造母函数：
化简得：
，其中 
， 为选出 i 个物品的排列方法数
注：若题中有限定条件，只需将第 i 项出现的列在第 i 项的式子中，未出现的不用列入
例如：物品 i 出现的次数为非 0 偶数，则原式改为：
3.实现
double num[15];//第i个物品有num[i]个
double a[15],b[15];
double fac(int n) { //求阶乘
double ans=1.0;
for(int i=1; i<=n; i++)
ans*=i;
return ans;
}
int main() {
int n,m;
while(scanf("%d%d",&n,&m)!=EOF) {
for(int i=1; i<=n; i++)
cin>>num[i];
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
for(int i=0; i<=num[1]; i++)//a[0]=1.0;
a[i]=1.0/fac(i);
for(int i=2; i<=n; i++) {
for(int j=0; j<=m; j++) {
for(int k=0; k<=num[i]&&j+k<=m; k++) {
b[j+k]+=a[j]/fac(k);
}
}
for(int j=0; j<=m; j++) {
a[j]=b[j];
b[j]=0;
}
}
printf("%.0lf\n",a[m]*fac(m));
}
return 0;
}【例题】
- Square Coins（HDU-1398）(n1为0,n2为无穷下的普通母函数)：点击这里
- Holding Bin-Laden Captive! （HDU-1085）(n1为0,忽视p的普通母函数)：点击这里
- 排列组合（HDU-1521）(指数型母函数)：点击这里