CodeForces - 1260F Colored Tree（树链剖分 + 组合计数 + 树状数组）

题意

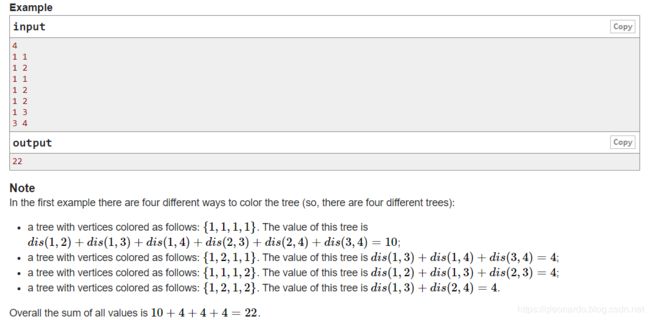
给你一棵n个节点的树，每个节点都有一个颜色。这棵树的权值定义为，任意两个相同颜色的点之间的路径长度之和。但是，这棵树的每个点的颜色是不确定的，你只知道节点$i$的颜色属于某一个区间$[l_i,r_i]$，于是这棵树总共就有${\prod }_{1\le i\le n}(r_i-l_i+1)$种可能。你需要求这么多种可能情况下的树的权值和。

做法

考虑枚举每一种颜色$c$，然后考虑维护颜色为$c$的点，由于每个点的颜色是一个区间，所以很容易维护。

考虑计算两个颜色相同点$i$和$j$的贡献$w=dis(i,j)\ast {\prod }_{k=1,k\ne i,k\ne j}^n(r_k-l_k+1)$，我们不妨设：
$$P=\prod _{i=1}^n(r_i-l_i+1),g_i=r_i-l_i+1$$
于是，有
$$\begin{array}{rl}w& =dis(i,j)\ast \frac{P}{g_i\ast g_j}\\ & =(dep[i]+dep[j]-2\ast dep[lca])\ast \frac{P}{g_i\ast g_j}\end{array}$$
我们考虑所有的点，对于一个颜色$c$，如果点$i$颜色也为$c$那么，$V[i]=1$否则$V[i]=0$，那么最后的答案可以等于
$$\begin{array}{rl}ans& =P\ast \sum _{i<j,V[i],V[j]}^n(\frac{dep[i]}{g_i\ast g_j}+\frac{dep[j]}{g_i\ast g_j}-2\ast \frac{dep[lca]}{g_i\ast g_j})\\ & =P\ast (\sum _{i,V[i]}^n\frac{dep[i]}{g_i}\sum _{j,V[j],i\ne j}^n\frac{1}{g_j}-2\ast \sum _{i<j,V[i],V[j]}^n\frac{dep[lca]}{g_i\ast g_j})\end{array}$$
对于前面那个东西，我们可以很容易的求出来，现在考虑如果求减号后面的东西。我们考虑把后面的东西拆成$\frac{dep[lca]}{g_i}\ast \frac{1}{g_j}$。

对于一个新加入的点$j$，我们先考虑它和之前加入的所有点的$lca$，我们用$\frac{1}{g_j}$乘上除了1以外从1到$x$的所有点的权值和$sum$。根据上面拆成的公式，$sum$应该等于$\frac{dep[lca]}{g_i}$的和。然后，我们再对从1到$j$的所有点都加上$\frac{1}{g_j}{g}_j$。现在我们再回头看，$sum$的数值恰好是我们想要的。

于是，我们只需要树链剖分一下，动态维护区间和即可。

#include
#define INF 0x3f3f3f3f
#define eps 1e-5
#define pi 3.141592653589793
#define LL long long
#define pb push_back
#define fi first
#define se second
#define lb lower_bound
#define ub upper_bound
#define bug(x) cerr<<#x<<"      :   "<
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;

const int mod = 1e9 + 7;
const int N = 100010;

struct EX_BIT                                   //支持区间修改、区间查询的树状数组
{
    struct binaryIndexTree
    {
        int c[N];
        void init(){memset(c,0,sizeof(c));}
        void update(int x,int k){for(;x<N;c[x]=(c[x]+k)%mod,x+=x&-x);}
        int sum(int x){int ans=0;for(;x>0;ans=(ans+c[x])%mod,x-=x&-x);return ans;}
    } BIT1,BIT2;

    void init(){BIT1.init();BIT2.init();}
    int getsum(int l,int r){return (sum(r)-sum(l-1)+mod)%mod;}
    void update(int l,int r,int x){add(l,x);add(r+1,(mod-x)%mod);}
    int sum(int x){return ((LL)(x+1)*BIT1.sum(x)%mod-BIT2.sum(x)+mod)%mod;}
    void add(int x,int k){BIT1.update(x,k);BIT2.update(x,(LL)x*k%mod);}
} BIT;

inline LL qpow(LL x,LL n)
{
    LL res=1;
    while(n)
    {
        if (n&1) res=res*x%mod;
        x=x*x%mod; n>>=1;
    }
    return res;
}

int id[N],top[N],son[N],sz[N],fa[N],dep[N],inv[N];
std::vector<int> l[N],r[N],g[N];
int idx,n,m;

inline void dfs1(int x,int d,int f)
{
    son[x]=0; dep[x]=d; sz[x]=1;
    for(int y:g[x])
        if (y!=f)
        {
            fa[y]=x;
            dfs1(y,d+1,x);
            sz[x]+=sz[y];
            if (sz[y]>sz[son[x]]) son[x]=y;
        }
}

inline void dfs2(int x,int f)
{
    top[x]=f; id[x]=++idx;
    if (son[x]) dfs2(son[x],f);
    for(auto y:g[x])
        if (y!=son[x]&&y!=fa[x]) dfs2(y,y);
}

inline int query(int u,int v)
{
    int tp1=top[u],tp2=top[v];
    int res=(mod-BIT.getsum(1,1))%mod;
    while (tp1!=tp2)
    {
        if (dep[tp1]<dep[tp2]){swap(tp1,tp2);swap(u,v);}
        res=(res+BIT.getsum(id[tp1],id[u]))%mod;
        u=fa[tp1]; tp1=top[u];
    }
    if (dep[u]>dep[v]) swap(u,v);
    return (res+BIT.getsum(id[u],id[v]))%mod;
}

inline void change(int u,int v,int x)
{
    int tp1=top[u],tp2=top[v];
    while (tp1!=tp2)
    {
        if (dep[tp1]<dep[tp2]){swap(tp1,tp2);swap(u,v);}
        BIT.update(id[tp1],id[u],x);
        u=fa[tp1]; tp1=top[u];
    }
    if (dep[u]>dep[v]) swap(u,v);
    BIT.update(id[u],id[v],x);
}

int main(int argc, char const *argv[])
{
    int P=1;
    sc(n); int mx=0;
    for(int i=1;i<=n;i++)
    {
        int x,y; scc(x,y);
        l[x].pb(i); r[y+1].pb(i);
        mx=max(mx,y);  inv[i]=qpow(y-x+1,mod-2);
        P=(LL)P*(y-x+1)%mod;
    }
    for(int i=1;i<n;i++)
    {
        int x,y; scc(x,y);
        g[x].pb(y); g[y].pb(x);
    }
    dfs1(1,0,0);
    dfs2(1,1);
    LL ans=0,s1=0,s2=0,s3=0,s4=0;
    for(int i=1;i<=mx;i++)
    {
        for(int x:r[i])
        {
            s1=(s1-(LL)dep[x]*inv[x]%mod+mod)%mod;
            s2=(s2-inv[x]+mod)%mod;
            s3=(s3-(LL)dep[x]*inv[x]%mod*inv[x]%mod+mod)%mod;
            change(1,x,mod-inv[x]);
            s4=(s4-(LL)inv[x]*query(1,x)%mod+mod)%mod;
        }
        for(int x:l[i])
        {
            s1=(s1+(LL)dep[x]*inv[x]%mod)%mod;
            s2=(s2+inv[x])%mod;
            s3=(s3+(LL)dep[x]*inv[x]%mod*inv[x]%mod)%mod;
            s4=(s4+(LL)inv[x]*query(1,x)%mod)%mod;
            change(1,x,inv[x]);
        }
        ans=(ans+s1*s2%mod-s3-2*s4)%mod;
        ans=(ans+mod)%mod;
    }
    printf("%lld\n",ans*P%mod);
    return 0;
}