Min25筛小结
关于筛法,最近看到了很多,也尝试的学了一些。总的来说可以分为线性筛和亚线性筛。
所谓线性筛,就是可以在线性时间复杂度内求解的筛法。而亚线性筛则是时间复杂度更为优秀的筛法,通常时间复杂度可以达到小于线性时间,可以解决1e8~1e11范围内的问题。
关于亚线性筛,之前已经写过了杜教筛,但是个人感觉用到的地方确实不太多,而且比较难构造。而这次要讲的Min25筛则相对要求的条件更低,而且不需要构造新的数论函数。另外还有一种亚线性筛叫洲阁筛,与Min25筛类似。
首先要弄清楚Min25筛具体用在什么地方,有什么使用条件。一般来说,它可以求大部分的积性函数的和,即形如:
要求的条件是![]() 要能够用多项式表示,而且
要能够用多项式表示,而且![]() 要能够快速计算。
要能够快速计算。
Min25筛的大致思想,就是把这个结果分为两个部分(准确来说是三个部分),一个是i为质数的和,一个是i为合数的和,再加上i为1的函数值。那么,我们首先看如果求这个i为质数部分的和ans1。我们不妨设
也即g(n,j)表示从1累加到n的F(i),其中的i要满足要么i自己是质数,要么i的最小质因子大于第j个质数。这样,显然有ans1等于g(n,|P|)。那么我们考虑如何去计算这个g(n,j)。
我们发现,当![]() 时,最小质因子是
时,最小质因子是![]() 的最小合数就是
的最小合数就是![]() ,而
,而![]() ,所以此时有
,所以此时有![]() 。
。
当![]() 时,我们考虑从g(n,j-1)转移到g(n,j)时少了什么东西,显然少了的就是最小质因子恰好是
时,我们考虑从g(n,j-1)转移到g(n,j)时少了什么东西,显然少了的就是最小质因子恰好是![]() 的和,所以要把这一部分给减去。还是考虑用g(x,y)来表示这一部分的结果,于是有:
的和,所以要把这一部分给减去。还是考虑用g(x,y)来表示这一部分的结果,于是有:
![]()
总的来说减去的部分本身也是两个部分,首先是要把![]() 这个最小质因子提出来,那么剩下的和就是
这个最小质因子提出来,那么剩下的和就是![]() ,但是这个里面还是包含了那些最小质因子小于
,但是这个里面还是包含了那些最小质因子小于![]() 的部分,而我们要求的是最小质因子恰好是
的部分,而我们要求的是最小质因子恰好是![]() 的和,所以还要减去最小质因子小于
的和,所以还要减去最小质因子小于![]() 的部分,这就是
的部分,这就是![]() 。
。
这样一来g(n,j)总的递推公式就是:
对于这个递推公式,![]() 显然等于
显然等于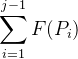 这个j的个数不会很多。而
这个j的个数不会很多。而![]() 最多只有
最多只有![]() 个取值,我们同样可以很快的求解。可以证明这里的复杂度不会很高。
个取值,我们同样可以很快的求解。可以证明这里的复杂度不会很高。
然后这里递推的起点是g(n,0),这个含义就是相当于把所有的数字当作质数,然后求 ![]() 要注意这里的求和与我们要做的最终答案的区别。这里其实是相当于
要注意这里的求和与我们要做的最终答案的区别。这里其实是相当于![]() ,因为我是把所有的数字当作了质数。更具体的说,作为积性函数,F(i)的表达式肯定是分段的,如果i是质数,那么会有一个通项公式,如果是合数,那么可以是各个质因子的乘积。这里把所有的数字当作质数就是把所用的数字去套i为质数时的通项公式再求和,这个求和一般都能手动化简为另一个通项公式作为递推的起点。
,因为我是把所有的数字当作了质数。更具体的说,作为积性函数,F(i)的表达式肯定是分段的,如果i是质数,那么会有一个通项公式,如果是合数,那么可以是各个质因子的乘积。这里把所有的数字当作质数就是把所用的数字去套i为质数时的通项公式再求和,这个求和一般都能手动化简为另一个通项公式作为递推的起点。
更加深入的理解这个过程,我们可以这样子理解。一开始,我是把所有的数字当作质数,然后后面j的循环,相当于一步步的从小到大把其他质数筛掉,和普通的埃氏筛类似,都是只需要筛到![]() 这个级别。
这个级别。
现在我们已经处理完了i为质数时的和,那么现在考虑直接求总和,考虑质数的和直接用,1的值单独算,主要是合数部分。与之前类似,我们令:
S(n,j)表示从1累加到n的F(i),同样的,i要么是质数,要么是质数,要么最小质因子大于j。与上面不同,我们这里要求的是倒过来的,最后需要的答案就是S(n,1)。类似的,我们可以得到下面的递推式:
关于这个前一部分![]() ,这个就是相应的质数部分的和,用所有质数的和,减去前j个质数。主要是后面这个合数部分。因为F(i)是积性函数,所以对于一个合数,我们可以把它的最小质因子包括其幂次的那一项提出来,提出来之后,剩下的部分就不包含这个最小质因子了,对应的和就是
,这个就是相应的质数部分的和,用所有质数的和,减去前j个质数。主要是后面这个合数部分。因为F(i)是积性函数,所以对于一个合数,我们可以把它的最小质因子包括其幂次的那一项提出来,提出来之后,剩下的部分就不包含这个最小质因子了,对应的和就是![]() 。然后这里e的范围是要求
。然后这里e的范围是要求![]() 因为要保证
因为要保证![]() ,这样最小质因子大于第k个数字。但是,注意到,这样子可以筛出大部分合数,但是对于形如
,这样最小质因子大于第k个数字。但是,注意到,这样子可以筛出大部分合数,但是对于形如![]() 这种合数,我们并没有计算到,所以我们单独把这个加上。
这种合数,我们并没有计算到,所以我们单独把这个加上。
还是一样,进行数论分块求和递推,就可以求出最后的S(n,1)。再把F(1)加上即可。
总的来说就是这样,分成质数、合数和1三个部分来做,时间复杂度很玄学的 ,当然我也不知道怎么得出来的,反正用就是了。具体实现的话,一般首先是会把
,当然我也不知道怎么得出来的,反正用就是了。具体实现的话,一般首先是会把![]() 个区间给预处理出来,然后递推解决。在计算S(n,j)的时候就用上递归。代码的话,可以参见我的其他文章。
个区间给预处理出来,然后递推解决。在计算S(n,j)的时候就用上递归。代码的话,可以参见我的其他文章。
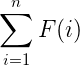
![\dpi{120} \large g(n,j)= \begin{cases} g(n,j-1) & P_j^2 > n \\ g(n,j-1)-F(P_j)[g(n/P_j,j-1)-g(P_j-1,j-1)] & P_j^2\le n \end{cases}](http://img.e-com-net.com/image/info8/5f18e03633bc47b49365ed4ba878ebde.gif)
![\large S(n,j)=\sum_{i=1}^nF(i)[min(p)\ge P_j,p\in P,p|i\ ]](http://img.e-com-net.com/image/info8/f7c01b5970c742a4ad83b54ad73fe6ee.gif)