matlab里的fft应用以及常用信号处理问题
matlab里的fft应用以及常用信号处理问题
1。什么是fft
FFT（Fast Fourier Transformation）就是快速傅里叶变换的意思。输入的是离散数据，输出的也是离散频率。
在matlab中具体常用的使用方法为X=fft(x)或X=fft(x,Ns)。
其中X输出是一组复数，abs值代表复数的幅值，angle值代表复数的相位，这一点以后会用到。
2。频率-幅值曲线图
用一个简单的函数去做频率-幅值曲线图，采用1hz和10hz的信号，加上一点噪声，构成输入信号。
t=1:0.01:10;
x=2*sin(2*pi*t)+1*sin(10*2*pi*t)+0.8*(rand(1,length(t))-0.5)+1;
figure(1)
plot(t,x)
Ns=length(t);%信号分析长度
fs=1/(t(2)-t(1));%信号采样频率
[freq,X_real,X_angle]=myfft(x,Ns,fs);%计算频率-幅值参数
figure(2)
plot(freq,X_real);%绘制频率-幅值曲线
function [freq,X_real,X_angle]=myfft(x,Ns,fs)
x=detrend(x);%消除曲线趋势(0次趋势和1次趋势）
X=fft(x,Ns);%fft
%计算频率索引号
n2=1:Ns/2+1;%加不加一无所谓,Ns为偶数
%计算真实幅值
X_real=abs(X(n2))*2/Ns;%除以N还是NS？(有效长度，小于等于N)
%计算分量相位
X_angle=angle(X(n2));
%设置频域刻度
freq = (0:Ns/2)*fs/Ns;
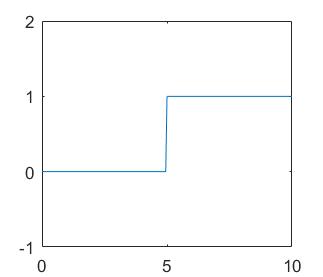
end输入时间-幅值图
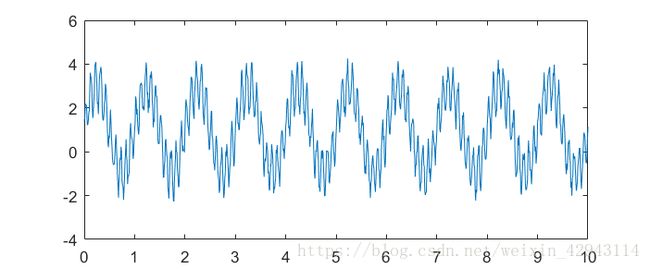
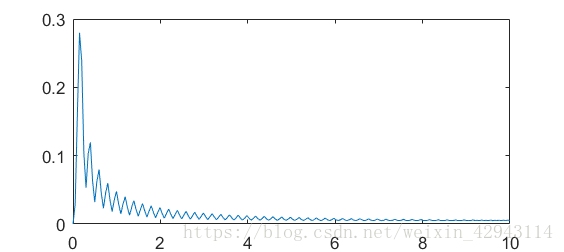
输出频率-幅值图
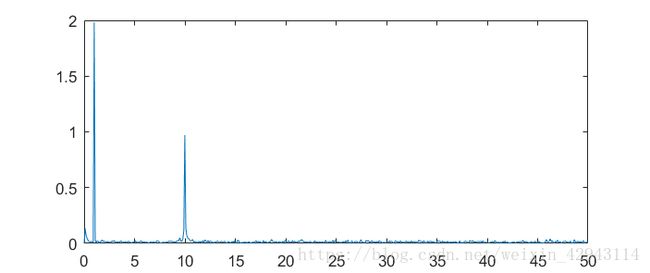
其中有几个参数必须要说明：
- 信号分析长度：一般取信号长度，或者2的整数次方长度。如果大于信号长度，matlab默认在信号后面补0。
- 信号采样频率：就是每秒钟信号的采样点，与信号采样间隔成倒数关系。
下面对 [freq,X_real,X_angle] = myfft(x,Ns,fs) 的算法进行说明。
1。首先要消除趋势项，示例效果如下：
0次趋势，或者称为常数项趋势：
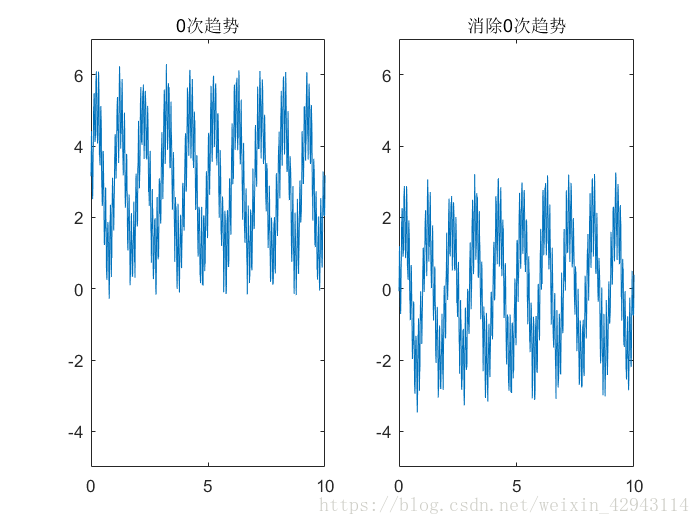
1次趋势，或者称为直线趋势：
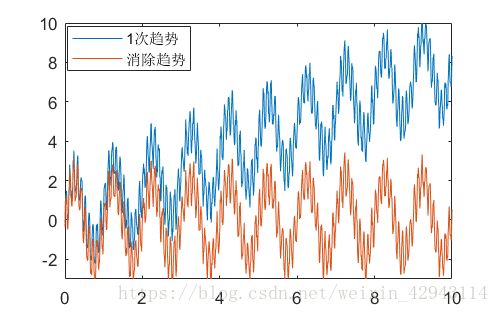
1次趋势如果不消除，会被fft当做一个巨大的频率很低的正弦波处理，此时在低频会出现异常信号。
2。fft
计算信号的fft，长度取信号长度。
3。计算频率索引号
fft得到的数据具有左右对称的特点，通常只采用左半边的数据作为信号数据。
同时提一句，fft得到的数据长度同Ns。
4。计算真实幅值
abs(X)/2*Ns这个是固定的，记住就行了，如果想知道为什么可以了解fft的具体算法。这里Ns取得是信号的有效长度，如果在信号末尾补0的话，不算做有效长度。
5。设置频域刻度
freq = (0:Ns/2)*fs/Ns;这个也是固定的用法。唯一注意的就是要和频率索引对应上。
通过计算可以看到，频率的最大值为fs/2，频率的分辨率为fs/Ns=1/T。
所以为了提高频率的最大值，需要提高信号的采样频率，这个主要是针对信号采样仪器设备的要求。
所以为了提高频率的分辨率，需要增加测量时间T，把信号尽可能测量的更长。
3。信号补零后的处理
之前在上一章节提到信号有时会进行补零处理，即在原有信号之后增加诺干个0。
根据上一章末尾的结论，补零可以增加信号的观测时间（虽然是假的），提高频率分辨率。
比如对于
t=0:0.01:1;
x=2*sin(8*2*pi*t)+1*sin(9*2*pi*t);
的输入
单纯的fft几乎无法分辨这两个信号的差异，因为频率分辨率为1hz，大于等于信号频率之差。
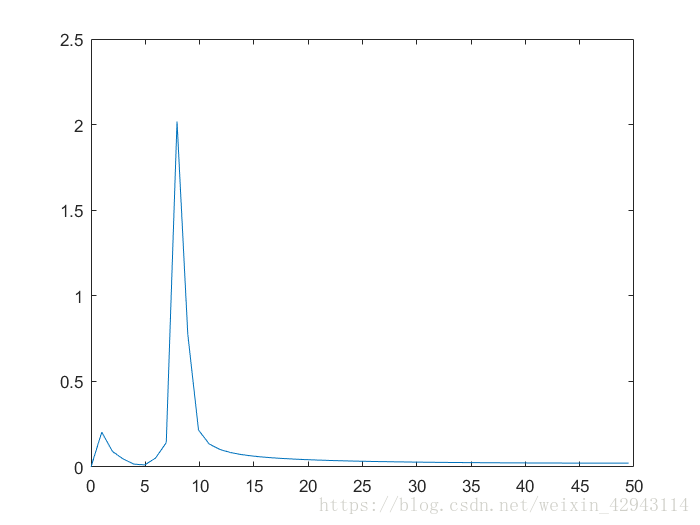
所以要在信号后面补零，另Ns=2*length(t)
t=0:0.01:1;
x=2*sin(8*2*pi*t)+1*sin(9*2*pi*t);
%figure(1)
%plot(t,x)
Ns=length(t)*2;%信号分析长度，*2补零
fs=1/(t(2)-t(1));%信号采样频率
[freq,X_real,X_angle]=myfft(x,Ns,fs);%计算频率-幅值参数%myfft函数到第一个例子里找
X_real=2*X_real;%信号有效长度的补偿
figure(2)
plot(freq,X_real);%绘制频率-幅值曲线得到的新频率分辨率为0.5hz。
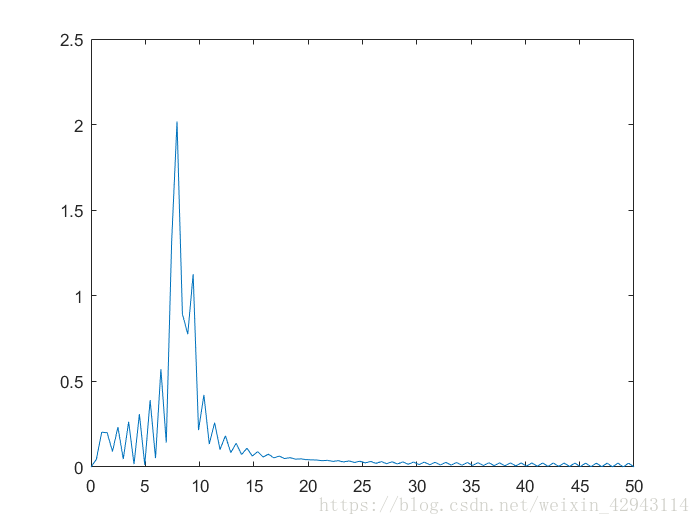
可以看到，最终两个信号被成功的区分了出来。
但是又发现在信号周围出现了很多规律的小鼓包，这个是由于补零之后输入信号产生了突变，造成的“信号泄露”。可以这么理解，傅里叶在处理光滑的周期信号时有着他的优点，但是在处理突变信号时就会产生很多小尖峰。
比如典型的0-1突变
它的fft最终结果如下：
下一章我们会更细致的去描述信号频谱泄露产生与消除方式。
4。信号频谱泄露
如果信号在没有能在时间窗口内出现整数个周期，就会出现信号的泄露。
下图是一个1hz的信号，没有在末尾处没有出现完整，得到的频谱图。
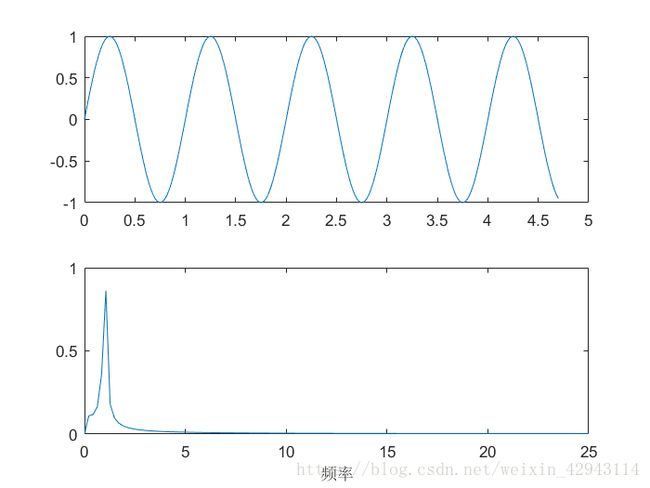
信号泄露会导致该频率峰值的减小，同时也会导致频率峰宽度的增加。如上图，频率峰值不是1，而是比1小，而且1hz在两侧很长一段距离衰减的都很慢。
由于实际测量中，很难测到正好整数个波长，所以我们可以考虑给信号做一定的处理来减小这个泄漏问题。
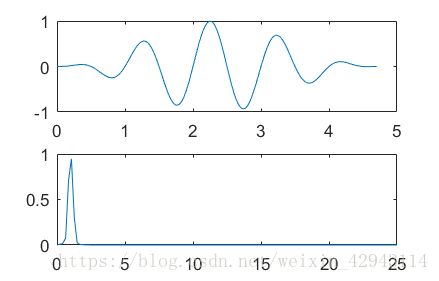
最常用的方法就是加窗，也就是说让信号从中间到两端缓慢减小，防止边缘函数值的突变。比如matlab里的hann窗
t=0:0.02:5;
t=t(1:end-15);
x=1*sin(1*2*pi*t);
figure(1)
subplot(2,1,1)
Ns=length(t);%信号分析长度
wind=hann(Ns)';%加hann窗'
x=wind.*x;
plot(t,x)
fs=1/(t(2)-t(1));%信号采样频率
[freq,X_real,X_angle]=myfft(x,Ns,fs);%计算频率-幅值参数%myfft函数到第一个例子里找
X_real=X_real*2;%加hann窗的补偿
subplot(2,1,2)
plot(freq,X_real);%绘制频率-幅值曲线
注意加窗之后，如果加窗之后，需要对最终幅值做一定的补偿。这个补偿值根据各种窗不同而不同。这里hann窗取2。
可以看到峰值更尖了，峰值达到了0.9，虽然并没有到1，但是也还好吧。
5。多段信号叠加消除随机噪声（降低频率分辨率）
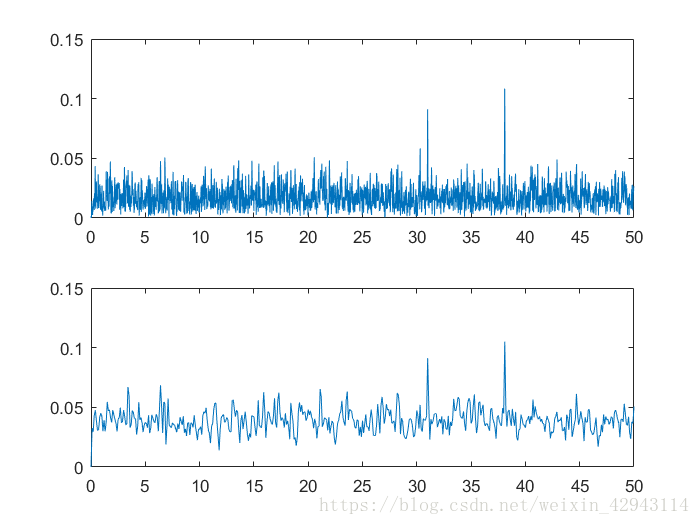
对于一个超长的信号，可以采用截取多段的方式去得到叠加的信号，以达到更改频率分辨率，消除随机信号的方法。
比如
t=0:0.01:50;
x=0.1*sin(31*2*pi*t)+0.1*sin(61.9*2*pi*t)+2*(rand(1,length(t))-0.5);
figure(1)
subplot(2,1,1)
Ns=length(t);%信号分析长度
wind=hann(Ns)';%加hann窗
xw=wind.*x;
fs=1/(t(2)-t(1));%信号采样频率
[freq,X_real,X_angle]=myfft(xw,Ns,fs);%计算频率-幅值参数
X_real=X_real*2;%有效长度的补偿
plot(freq,X_real);%绘制频率-幅值曲线
[freq,X_real1,X_angle]=myfft(x(1:1000).*hann(1000)',1000,fs);
[freq,X_real2,X_angle]=myfft(x(1001:2000).*hann(1000)',1000,fs);
[freq,X_real3,X_angle]=myfft(x(2001:3000).*hann(1000)',1000,fs);
[freq,X_real4,X_angle]=myfft(x(3001:4000).*hann(1000)',1000,fs);
[freq,X_real5,X_angle]=myfft(x(4001:5000).*hann(1000)',1000,fs);
subplot(2,1,2)
plot(freq,(X_real1+X_real2+X_real3+X_real4+X_real5)/5*2);用这种方法可以得到较低频率分辨率的图像，因为有时候较高频率分辨率的随机信号不是我们想要得到的。
