2020牛客多校暑期训练营（第五、六场）

快速清一下进度。。回头细补

第五场

D.Drop-Voicing

算法标签：LIS

经过一些观察之后把问题转换成：“最少移动多少个数使得环有序”，也就是要找出原环的最长递增子序列（LIS）。打的时候因为n比较小直接$O(n^3)$过了，但是通过二分或者树状数组其实是可以压到$O(n^{2}logn)$的

参考：最长上升子序列(LIS)的三种求法

#include
using namespace std;
typedef long long ll;

const int N=1000+5,INF=0x3f3f3f3f;

int T,n,m,A[N],dp[N],ans;

int check(int l,int r)
{
	for (int i=l;i<r;i++)
	{
		int j=lower_bound(dp,dp+n,A[i])-dp;
		dp[j]=A[i];
	}
	return n-(lower_bound(dp,dp+n,INF)-dp);
}
int main()
{
	cin>>n;
	for (int i=0;i<n;i++)
	{
		scanf("%d",&A[i]);
		A[n+i]=A[i];
	}
	ans=INF;
	for (int k=0;k<n;k++)
	{
		memset(dp,INF,sizeof(dp));
		ans=min(ans,check(k,k+n));
	}
	cout<<ans;
	return 0;
}

B.Graph

算法标签：字典树、异或最小生成树、Boruvka算法

同样先观察到无论如何操作，树上任意两点连边的权值是固定的。于是可以任意选取一个结点作为根（比如0结点），通过dfs求出每个点到根节点路径的异或和，将其作为点的权值，那么任意两点连边的权值就等同于这两点权值的异或。

此时问题就变成求异或最小生成树了。

解决方法是通过字典树和Boruvka算法的思想。

先读了读代码了解一下Boruvka算法是个啥。Boruvka算法介绍

但其实更多的还是借用了它的思想，即对于某个联通块（一开始每个节点各自属于独立的联通块），我们可以贪心地找到所有从该联通块指向其他联通块的权值最小的边，并直接将它加入最小生成树中。

把这个思想运用到字典树中，其实就变成了子树合并的问题。把一个结点的左右子树分别看作两个联通块，对于这两个联通块，当前权值最小的边一定同时连接了这两个联通块。那么借助字典树，尽可能在往下走走一样的方向，就可以找到这条边的权值了。

对于权值重复的点，肯定会在第一步就互相连边，由于这些边权值一定是0，可以忽略，所以只需要直接去重就可以了。

因为这里字典树只有0和1，所以直接用l和r存左右儿子了。通用的字典树写法之后再补。

#include
using namespace std;
typedef long long ll;
const int N=1e5+5;
const int INF=0x3f3f3f3f;

int l[N<<5],r[N<<5];

struct Edge{
    int t,w;
};

int root,num;

vector<Edge>G[N];

vector<int>P;

int u,v,w,n;

ll tot;

void dfs(int x,int fa,int now)
{
    P.push_back(now);
    for (auto to:G[x])
    {
        if (to.t!=fa)
            dfs(to.t,x,now^to.w);
    }
}
void MakeTrie(int subroot,int check,int x)
{
    if (check==0) return;
    if ((x&check)==0)
    {
        if (l[subroot]==0) l[subroot]=++num;
        MakeTrie(l[subroot],check>>1,x);
    }
    else
    {
        if (r[subroot]==0) r[subroot]=++num;
        MakeTrie(r[subroot],check>>1,x);
    }
}
ll dfs3(int a,int b,int check)
{
	if (!a || !b) return INF;
    if (check==0) return 0;
    ll t1,t2;
    t1=min(dfs3(l[a],l[b],check>>1),dfs3(r[a],r[b],check>>1));
    if (t1==INF)
		t2=check+min(dfs3(l[a],r[b],check>>1),dfs3(r[a],l[b],check>>1));
	else t2=INF;
    return min(t1,t2);
}
ll dfs2(int subroot,int check)
{
    ll ret=0;
    if (l[subroot]) ret+=dfs2(l[subroot],check>>1);
    if (r[subroot]) ret+=dfs2(r[subroot],check>>1);
    if (l[subroot] && r[subroot])
    {
        int t1=l[subroot],t2=r[subroot];
        ret+=check+dfs3(t1,t2,check>>1);
    }
    return ret;
}

int main()
{
    cin>>n;
    for (int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        G[u].push_back({v,w});
        G[v].push_back({u,w});
    }
    dfs(0,-1,0);
    sort(P.begin(),P.end());
    P.erase(unique(P.begin(),P.end()),P.end());
    for (auto x:P)
    {
        MakeTrie(0,1<<30,x);
    }
    printf("%lld\n",dfs2(0,1<<30));
    return 0;
}

第六场

G.Grid-Coloring

算法标签：构造

其实感觉是比较宽松的构造题，比赛的时候没想到判n==1的情况，调了一个多小时没发现，赛后加上就过了，有点伤。。我个人的思路是先用红蓝两种颜色染色，只要每行每列颜色都是交替的就肯定能满足条件了。

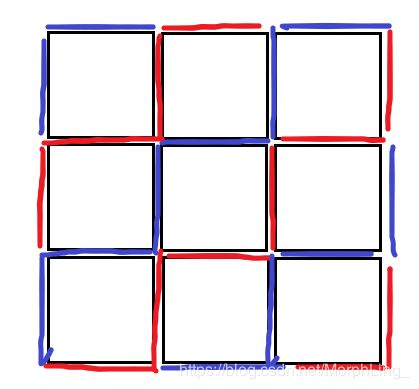
然后再用把某一部分蓝色或者红色改变成其他颜色，因为只要保证这个颜色只从蓝色或者只从红色改变而来，改变之后肯定还是满足条件的。

对于k是偶数的情况，恰好可以一半给蓝色，一半给红色，但对于k是奇数的情况，就不可避免会有一种颜色同时从蓝色红色改变而来。此时只需要考虑怎么安排这一种颜色就可以了。。答案是一半选择水平的蓝色，一半选择竖直的红色。对于剩下的，再按照k为偶数的情况分配即可。具体证明涉及一点数学计算，主要是奇偶性方面的，其实也不难推，这里就不浪费时间了。

#include
using namespace std;
typedef long long ll;
const int N=1e5+5;

int col[N];

int n,k,T;

void sol()
{
	cin>>n>>k;
	int sum=2*n*(n+1);
	for (int i=1;i<=sum;i++) col[i]=0;
	if (sum%k!=0 || k==1 || n==1)
	{
		printf("-1\n");
		return;
	}

	int t1=1,t2=sum/2+1;
	if (k%2==1)
	{
		int tot=sum/k;
		for (int i=1;i<=tot/2;i++) col[i]=k,col[i+sum/2]=k;
		t1+=tot/2;
		t2+=tot/2;
	}
	for (int i=1;i<=k/2*2;i++)
	{
		if (t1<=sum/2)
		{
			for (int j=1;j<=sum/k;j++)
			{
				col[t1]=i;
				t1++;
			}
		}
		else
		{
			for (int j=1;j<=sum/k;j++)
			{
				col[t2]=i;
				t2++;
			}
		}
	}
	t1=1,t2=sum;
	int last=1;
	for (int i=1;i<=n+1;i++)
	{
		for (int j=1;j<=n;j++)
		{
			if (last==1)
			{
				printf("%d",col[t1]);
				if (j!=n) printf(" ");
				t1++;
				last=2;
			}
			else
			{
				printf("%d",col[t2]);
				if (j!=n) printf(" ");
				t2--;
				last=1;
			}
		}
		if (n%2==0) last=3-last;
		printf("\n");
	}
	last=1;
	for (int i=1;i<=n+1;i++)
	{
		for (int j=1;j<=n;j++)
		{
			if (last==1)
			{
				printf("%d",col[t1]);
				if (j!=n) printf(" ");
				t1++;
				last=2;
			}
			else
			{
				printf("%d",col[t2]);
				if (j!=n) printf(" ");
				t2--;
				last=1;
			}
		}
		if (n%2==0) last=3-last;
		printf("\n");
	}
}

int main()
{
	cin>>T;
	while(T--) sol();
	return 0;
}

H.Harmony-Pairs

算法标签：数位dp

正好有机会学一下数位dp。
数位dp总结 之 从入门到模板

之前一直望而却步，学了一下感觉其实也不是很难理解，但是做题要能熟练用就是另一回事了。

dp[pos][del][eqb][eqa] pos表示当前的数位，del表示当前a和b数位和之差（避免负数取2500为零点），eqb表示当前B是否取到N的最大值，eqa表示当前A是否取到B的最大值。通过eqb和eqa决定转移时数位取值范围。这样一来最终的状态个数也是很有限的。

#include
using namespace std;
const int MOD=1e9+7;

int digit[20];
int dp[200][5000][2][2];
char n[200];

int dfs(int pos,int del,int eqb,int eqa)
{
	if (pos==-1)
	{
		if (del>2500)
			return 1;
		else return 0;
	}
	if (dp[pos][del][eqb][eqa]!=-1) return dp[pos][del][eqb][eqa];
	int upb=eqb?n[pos]:9;
	int sum=0;
	for (int b=0;b<=upb;b++)
	{
		for (int a=0;a<=(eqa?b:9);a++)
		{
			sum=(sum+dfs(pos-1,del+a-b,eqb&&(b==n[pos]),eqa&&(a==b)))%MOD;
		}
	}
	dp[pos][del][eqb][eqa]=sum;
	return sum;
}

int main()
{
	scanf("%s",n);
	int len=strlen(n);
	reverse(n,n+len);
	for (int i=0;i<len;i++) n[i]-='0';
	memset(dp,-1,sizeof(dp));
	printf("%d",dfs(len-1,2500,1,1));
	return 0;
}