扩展欧几里德算法解二元一次不定方程

扩展欧几里德算法：

已知两个不完全为 0 的非负整数 a，b，必然存在整数对 x，y ，使它们满足贝祖等式：

解一定存在，根据数论中的相关定理。下面给出代码：

int extgcd(int a, int b, int& x, int& y) {
    int gcd = a;
    if (b != 0) {
        gcd = extgcd(b, a % b, y, x);
        y -= (a / b) * x;
    }
    else {
        x = 1; y = 0;
    }
    return gcd;
}

解二元一次不定方程(ax + by = c)：

扩展欧几里德算法很大的一个用处就是在解不定方程。在计算时一般先是求出一对特解，再根据x与y的变化比例，构造通解。

注意我们求的所有解，都是整数解。

我们先计算   的解，等式两边同时乘以

  

 原式子就被构造成

所以就求出了不定方程的一对特解

这里不存在  不是整数的情况，因为当  时，方程不存在整数解，不在考虑范围内。

证明：

若 ，则  非整数

求一组特解代码：

bool Indefinite_equation(int a, int b, int n, int& x, int& y) {    //求一组特解
    int gcd = extgcd(a, b, x, y);       
    if (n % gcd) return false;
    int k = n / gcd;
    x *= k;
    y *= k;
    return true;
}

现在我们来考虑构造通解( 特解是X、Y )：

由于已经满足  , 两个未知数的关系类似于加权和固定，若一个增大，则另一个一定按比例减小，显然满足关系：

X 每变化 b 的整数倍，Y 就反向变化 a 的同等倍数。似乎构造出了通解表达式  、 。

但是我们会发现一个问题，就是 a 、b 不一定是最小的步长，可能会 “跳过” 许多解。

为了求得最小步长，我们应该对 a 、b 同时除以某个整数，使得商也是整数，就求出了每次最小的变化量。很明显，应除以

所以，通解应该是

 

求特殊的解：

最大/最小解

很多情况下，我们需要求的是 x 或 y 的最小正整数解。这里以 x 的最小解为例：

有一种方案是在求出特解的基础上，进行一个循环

• 当特解大于零时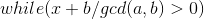：   ，x每次减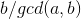 
• 当特解不大于零时：  ，x每次加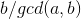 

但是这个方法存在效率问题，因为  可能远小于 x , 达到退出循环条件需要花很长时间。这里我采用的是取模的方法

• 当特解大于零时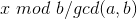：   便是小正整数解
• 当特解不大于零时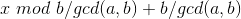：  便是小正整数解

x 与 y 最接近的解

以求 x < y时 , x 与 y 最接近的解为例。通过 y - x 的值来考虑。设 x , y 的步长分别是 dx , dy ，则 y - x 的最短步长为 dx + dy。

• 当特解 X < Y 时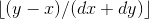，  便是通解中 n 的值
• 当特解 X > Y 时, 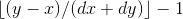   便是通解中 n 的值。但若  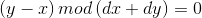时，不需要减 1 

附上代码：

//求 x < y 时，x, y 最接近的解
bool Indefinite_equation(int a, int b, int n, ll& x, ll& y) {      
    int gcd = extgcd(a, b, x, y);
    if (n % gcd) return false;                         //无整数解
    int k = n / gcd, dx = b / gcd, dy = a / gcd;       //dx,dy分别为对应的最小变化值
    x *= k;
    y *= k;                                            //此为某特解
    ll cnt = (y - x) / (dx + dy);
    if (cnt < 0 && (y - x) % (dx + dy)) cnt --;        //处理x>y的情况
    x += dx * cnt;
    y -= dy * cnt;
    return true;
}