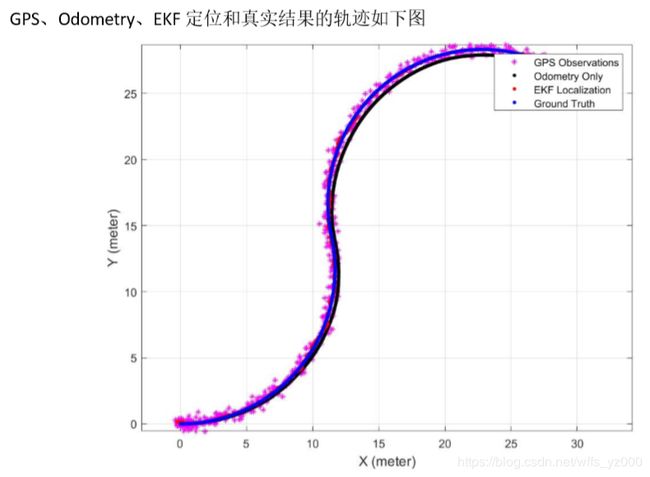
基于EKF（拓展卡尔曼滤波器）的机器人定位（MATLAB编程）

1 EKF原理

EKF是在KF的基础上，增加了对线性要求的拓展，即可以采用非线性函数表示运动方程和观测方程。
EKF的基本思想如下：

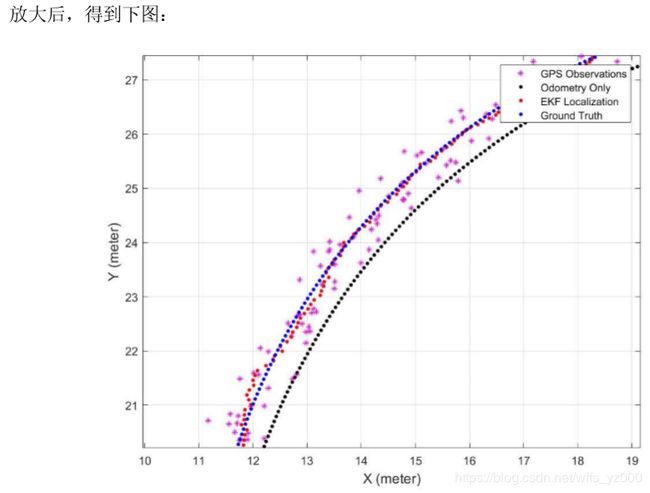
2 程序结果

Odometry表示里程计模型。

3 程序代码

function [] = ekf_localization()
    close all;
    clear all;

    disp('EKF Start!')

    time = 0;
    global endTime; % [sec]
    endTime = 60;
    global dt;
    dt = 0.1; % [sec]

    removeStep = 5;

    nSteps = ceil((endTime - time)/dt);

    estimation.time=[];
    estimation.u=[];
    estimation.GPS=[];
    estimation.xOdom=[];
    estimation.xEkf=[];
    estimation.xTruth=[];

    % State Vector [x y yaw]'
    xEkf=[0 0 0]';
    PxEkf = eye(3);

    % Ground True State
    xTruth=xEkf;

    % Odometry Only
    xOdom=xTruth;

    % Observation vector [x y yaw]'
    z=[0 0 0]';

    % Simulation parameter
    global noiseQ
    noiseQ = diag([0.1 0 degreeToRadian(10)]).^2; %[Vx Vy yawrate]

    global noiseR
    noiseR = diag([0.5 0.5 degreeToRadian(5)]).^2;%[x y yaw]
    
    % Covariance Matrix for motion
    convQ=eye(3);
    
    % Covariance Matrix for observation
    convR=noiseR;

    % Other Intial
    xPred = [0 0 0]';
    F = zeros(3);
    H = zeros(3);
    
    % Main loop
    for i=1 : nSteps
        time = time + dt;
        % Input
        u=robotControl(time);
        % Observation
        [z,xTruth,xOdom,u]=prepare(xTruth, xOdom, u);

        % ------ Kalman Filter --------
        % Predict
        xPred =  doMotion(xEkf, u);
        F = jacobF(xEkf, u);
        convQ = F*convQ*F'+ noiseQ;     
        
        % Update
        H = jacobH(xPred);
        PxEkf = convQ*H'*inv(H*convQ*H'+convR);
        xEkf= doObservation(z, xPred,PxEkf);
        convQ=(eye(3)-PxEkf*H)*convQ; 

        % -----------------------------
        % Simulation estimation
        estimation.time=[estimation.time; time];
        estimation.xTruth=[estimation.xTruth; xTruth'];
        estimation.xOdom=[estimation.xOdom; xOdom'];
        estimation.xEkf=[estimation.xEkf;xEkf'];
        estimation.GPS=[estimation.GPS; z'];
        estimation.u=[estimation.u; u'];

        % Plot in real time
        % Animation (remove some flames)
        if rem(i,removeStep)==0
            %hold off;
            plot(estimation.GPS(:,1),estimation.GPS(:,2),'*m', 'MarkerSize', 5);hold on;
            plot(estimation.xOdom(:,1),estimation.xOdom(:,2),'.k', 'MarkerSize', 10);hold on;
            plot(estimation.xEkf(:,1),estimation.xEkf(:,2),'.r','MarkerSize', 10);hold on;
            plot(estimation.xTruth(:,1),estimation.xTruth(:,2),'.b', 'MarkerSize', 10);hold on;
            axis equal;
            grid on;
            drawnow;
            %movcount=movcount+1;
            %mov(movcount) = getframe(gcf);% アニメーションのフレームをゲットする
        end 
    end
    close    
    finalPlot(estimation);
end

% control
function u = robotControl(time)
    global endTime;
    T = 10; % sec
    Vx = 1.0; % m/s
    Vy = 0.2; % m/s
    yawrate = 5; % deg/s
    
    % half
    if time > (endTime/2)
        yawrate = -5;
    end
    
    u =[ Vx*(1-exp(-time/T)) Vy*(1-exp(-time/T)) degreeToRadian(yawrate)*(1-exp(-time/T))]';
    
end

% all observations for 
function [z, xTruth, xOdom, u] = prepare(xTruth, xOdom, u)
    global noiseQ;
    global noiseR;

    % Ground Truth
    xTruth=doMotion(xTruth, u);
    % add Motion Noises
    u=u+noiseQ*randn(3,1);
    % Odometry Only
    xOdom=doMotion(xOdom, u);
    % add Observation Noises
    z=xTruth+noiseR*randn(3,1);
end

%Motion Model
function x = doMotion(x, u)
    global dt;
    %
    x_last = u;
    u_tran = u;
    x_last(1,:) = sqrt(u(1,:)^2+u(2,:)^2);
    x_last(2,:) = 0;
    x_last(3,:) = u(3,:);
    u_tran(1,:) = -x_last(1,:)/x_last(3,:)*sin(x(3,:))+x_last(1,:)/x_last(3,:)*sin(x(3,:)+dt*x_last(3,:));
    u_tran(2,:) = x_last(1,:)/x_last(3,:)*cos(x(3,:))-x_last(1,:)/x_last(3,:)*cos(x(3,:)+dt*x_last(3,:));
    u_tran(3,:) = dt*x_last(3,:);
    x = x + u_tran; 
end

% Jacobian of Motion Model
function jF = jacobF(x, u)
    global dt;
    %
    x_last = u;
    x_last(1,:) = sqrt(u(1,:)^2+u(2,:)^2);
    x_last(2,:) = 0;
    x_last(3,:) = u(3,:);
    jF = [1,0,-x_last(1,:)/x_last(3,:)*cos(x(3,:))+x_last(1,:)/x_last(3,:)*cos(x(3,:)+dt*x_last(3,:)); 
        0,1,-x_last(1,:)/x_last(3,:)*sin(x(3,:))+x_last(1,:)/x_last(3,:)*sin(x(3,:)+dt*x_last(3,:)); 
        0,0,1];        
end

%Observation Model
function x = doObservation(z, xPred,PxEkf)
    %
    x = xPred+PxEkf* (z-xPred);
 end

%Jacobian of Observation Model
function jH = jacobH(x)
    %
    jH = [1,0,0;
        0,1,0;
        0,0,1];
end

% finally plot the results
function []=finalPlot(estimation)
    figure;
    
    plot(estimation.GPS(:,1),estimation.GPS(:,2),'*m', 'MarkerSize', 5);hold on;
    plot(estimation.xOdom(:,1), estimation.xOdom(:,2),'.k','MarkerSize', 10); hold on;
    plot(estimation.xEkf(:,1), estimation.xEkf(:,2),'.r','MarkerSize', 10); hold on; 
    plot(estimation.xTruth(:,1), estimation.xTruth(:,2),'.b','MarkerSize', 10); hold on;
    legend('GPS Observations','Odometry Only','EKF Localization', 'Ground Truth');

    xlabel('X (meter)', 'fontsize', 12);
    ylabel('Y (meter)', 'fontsize', 12);
    grid on;
    axis equal;
    
    % calculate error
    % 
    figure(2);
    title('里程计误差和Ekf定位误差');
    hold on;
    nSteps = 600;
    index = [];
    error_Odom = [];
    error_Ekf = [];
    sum_Odom = 0;
    sum_Ekf = 0;
    for i=1:nSteps
        error_Odom = [error_Odom sqrt( (estimation.xOdom(i,1)- estimation.xTruth(i,1))^2+(estimation.xOdom(i,2)-estimation.xTruth(i,2))^2)];
        error_Ekf = [error_Ekf sqrt( (estimation.xEkf(i,1)- estimation.xTruth(i,1))^2+(estimation.xEkf(i,2)-estimation.xTruth(i,2))^2)];
        index = [index i];
    end
    for i=1:nSteps
        sum_Odom = sum_Odom + error_Odom(1,i);
        sum_Ekf = sum_Ekf + error_Ekf(1,i);
    end
    
    error_Odom_average = sum_Odom/nSteps;
    disp("纯里程计的误差为");
    disp(['error_Odom_average = ',num2str(error_Odom_average)]);
    
    error_Ekf_average = sum_Ekf/nSteps;
    disp("Ekf定位的误差为");
    disp(['error_Ekf_average = ',num2str(error_Ekf_average)]);
    
    % 画图：每个状态的里程计误差和Ekf定位误差
    plot(index(1,:),error_Odom(1,:))
    hold on;
    plot(index(1,:),error_Ekf(1,:));
    hold on;
    legend('error of Odom','error of Ekf');
end

function radian = degreeToRadian(degree)
    radian = degree/180*pi;
end

4 估计误差

EKF模型、里程计模型（Odometry）估计的误差分别为：（与真实值比较）

结论:

可以看出，EKF模型、里程计模型（Odometry）估计的误差变化趋势不同。
EKF模型估计的误差总体趋势平稳，稳定在一定范围内；
而里程计模型（Odometry）估计的误差会随着时间不断增加，最后达到无法满足实验要求。