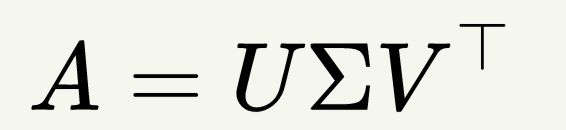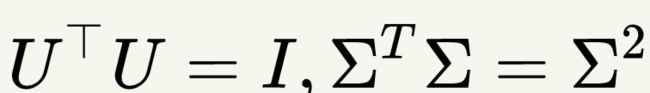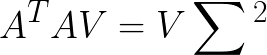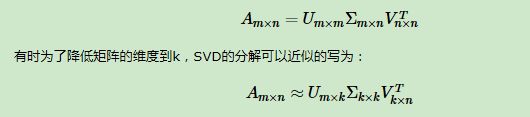SVD奇异值分解笔记
奇异值分解(Singular Value Decomposition)是机器学习领域广泛应用的算法,可以用于降维,推荐系统,自然语言处理等领域。
1、SVD定义
基本公式:
如上U,V是酉矩阵,酉矩阵定义为:
 为非主对角线上的元素值都为0,主对角线上的每个元素都称为奇异值。
为非主对角线上的元素值都为0,主对角线上的每个元素都称为奇异值。
2、特征值与特征向量
Ax=λx (式-1)
如上式,A为n阶矩阵,x为非零向量,λ为常数,则称λ为A的特征值,x为A的特征向量
对于多个λ特征值,则有一个特征向量矩阵,得到如下公式
如果不太了解特征值和特征向量概念,可以看如下链接,还有一个例子,一看便一目了然
https://blog.csdn.net/a727911438/article/details/77531973
3、关于U和V的一些解释与理解
3.1 右奇异矩阵V
V又叫做右奇异矩阵,V实际上为矩阵![]() (注意,意思是这是一个新的矩阵)得所有特征向量构成的矩阵。
(注意,意思是这是一个新的矩阵)得所有特征向量构成的矩阵。
证明:
上式证明使用了
将上式-3中,将左右同时乘以V矩阵,则有
上式是不是很熟悉了,参考式-2,证明了V为所有特征向量构成的矩阵,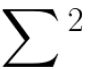 为所有特征值构成矩阵。
为所有特征值构成矩阵。
3.2 左奇异矩阵U
U又叫左奇异矩阵,U实际上为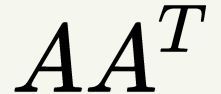 矩阵的所有特征向量构成的矩阵,证明可以参考上面右奇异矩阵V的证明。
矩阵的所有特征向量构成的矩阵,证明可以参考上面右奇异矩阵V的证明。
这里参考了 https://zhuanlan.zhihu.com/p/32600280
4.SVD的一些性质
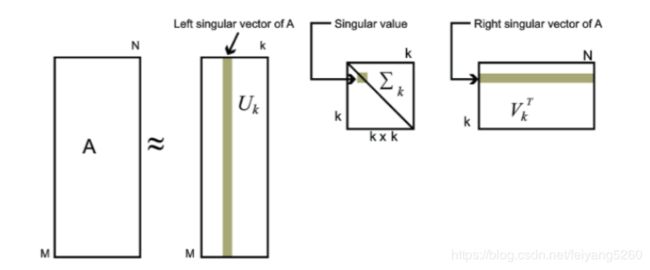
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说:
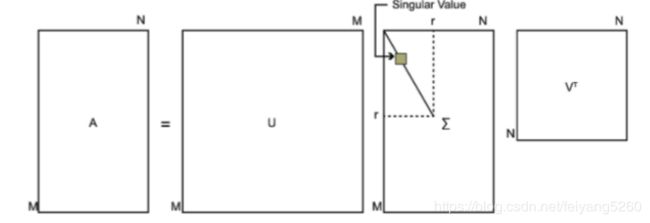
其中k要比n小很多,也就是一个大的矩阵A可以用三个小的矩阵
来表示。如下图所示,现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。
由于这个重要的性质,SVD可以用于PCA降维,来做数据压缩和去噪。也可以用于推荐算法,将用户和喜好对应的矩阵做特征分解,进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法,比如潜在语义索引(LSI)。
这段参考:https://blog.csdn.net/guoxinian/article/details/71078002
5、利用python实现SVD例子
from numpy import *
arr = array([ [1,2],[3,4],[5,6],[7,8] ])
U,Sigma,VT = linalg.svd(arr)
print('U=')
print(U)
print('Sigma=')
print(Sigma)
print('Sigma的维度')
print(Sigma.shape)
print('VT=')
print(VT)结果如下:U是一个4行4列的矩阵,VT是2行2列的矩阵,Sigma维度为2行2列,这里理解是只显示了对角线的值,非对角线上都为0。(根据SVD公式应该是4行2列,后两行为0来理解了)。
注意:在Sigma中第一个奇异值为14.2690955,远大于后面的数,实际在在工程中,有这么一个事实:前10%或前1%的奇异值之和便很接近所有奇异值之和了,因此,选取某个数目r的奇异值就好了,这意味着数据集中仅有r个重要特征,其余的都是噪声和冗余,这便实现了一个降维去噪的过程。
从NLP中LSI(潜在语义解析)中理解上述矩阵,arr是输入的4篇文档(2列保存的是词频,这里假设一篇文档只有两个单词的词频),
U中矩阵反映的是词与词之间的相关性,VT如上例子,2行2列,1列便表示一篇文档,一篇文档中词的2个单词,1行对应1个特征值,根据奇异值大小从上往下递减。(这里只有2篇文档(输入是4篇),我的理解是线性代数上说就是行列式转换,业务上理解就是对文档进行了一个去重)
按下面的方式降维,假设奇异值只取第一个14.2690995,则VT一篇文档中只以第一个单词,作为文档的代表。进而可以依次来计算相似度进行分类,
描述的可能不是太详细,可以看看这篇文章:https://www.cnblogs.com/pinard/p/6805861.html