Leetcode刷题——数组与字符串篇
二维数组:
498-对角线遍历:
方法1:效率低下

找二维数组的行与列之和的索引规律。
错误提示:Process finished with exit code 139 (interrupted by signal 11: SIGSEGV)
原因:初始化容器的时候未指定长度(vector order;),后面赋值时用到了order[i],这是不允许的,可以用函数emplace_back()或者push_back()来把值放入容器。
错误提示:reference binding to null pointer of type ‘std::vector
原因:未考虑空容器情况,首先,判断vector
class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
vector<int> order;
int row=matrix.size();
if(row==0){
return order;
}
int col=matrix[0].size();
if(col==0){
return order;
}
int n=0,m=0,sum=row*col;
for(int i=0;i<sum;i++){
order.emplace_back(matrix[n][m]);
cout<<order[i]<<endl;
if ((n+m)%2==0) {//斜向上
if (m==col-1) {//向右边
n++;
} else if (n == 0) {//向下边
m++;
} else {//右上
n--;m++;
}
}
else{//斜向下
if(n==row-1){//向右边
m++;
}else if(m==0){//向下边
n++;
}else{//左下
n++;m--;
}
}
}
return order;
}
};
54-螺旋矩阵:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]
思路:这里的方法不需要记录已经走过的路径,所以执行用时和内存消耗都相对较小
1)首先设定上下左右边界;
2)其次向右移动到最右,此时第一行因为已经使用过了,可以将其从图中删去,体现在代码中就是重新定义上边界;
3)判断若重新定义后,上下边界交错,表明螺旋矩阵遍历结束,跳出循环,返回答案;
4)若上下边界不交错,则遍历还未结束,接着向下、向左、向上移动,操作过程与第一,二步同理;
5)不断循环以上步骤,直到某两条边界交错,跳出循环,返回答案。
6)别忘了空数组的情况。
注意:在判断条件中使用++u等都会改变u的数值。
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector <int> ans;
if(matrix.empty()) return ans; //若数组为空,直接返回答案
int u = 0; //赋值上下左右边界
int d = matrix.size() - 1;
int l = 0;
int r = matrix[0].size() - 1;
while(true)
{
for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); //向右移动直到最右
if(++ u > d) break; //重新设定上边界,若上边界大于下边界,则遍历遍历完成,下同
for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); //向下
if(-- r < l) break; //重新设定有边界
for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); //向左
if(-- d < u) break; //重新设定下边界
for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); //向上
if(++ l > r) break; //重新设定左边界
}
return ans;
}
};
118-杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
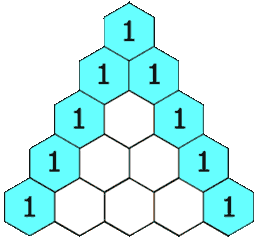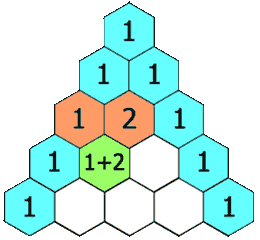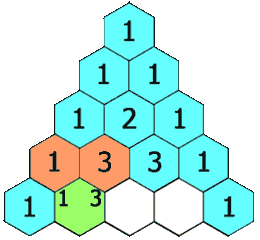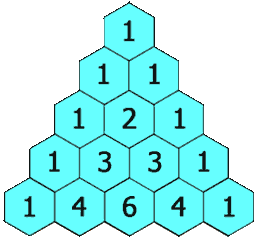
思路:首先画出三角的每个元素的索引,找到对应关系。
1)首先判断输入是否为0,是则直接输出;
2)输入即是行数(每一行单独用容器存储),而列数随着行数的增加而增加,进行遍历(跳出循环条件需要注意);
3)判断是否为行首或行尾,是则赋值为1;否则,当行数大于2行时,赋值为前一行相邻元素之和;
4)将每行都插入容器;
5)输出。
注意:遍历循环的内循环判断条件中含有变量m而不是常量numRows
class Solution {
public:
vector<vector<int>> generate(int &numRows) {
vector<vector<int>> order;
if(numRows==0) return order;
for(int m=0;m<numRows;m++){
vector<int> temp;
for(int n=0;n<m+1;n++){
if(n==0 || n==m) temp.emplace_back(1);
else temp.emplace_back(order[m-1][n]+order[m-1][n-1]);
}
order.emplace_back(temp);
}
return order;
}
};
字符串:
67-二进制求和,满二进一
给你两个二进制字符串,返回它们的和(用二进制表示)。输入为 非空 字符串且只包含数字 1 和 0。
思路:关键在与进位的程序处理
1)首先让两个字符串等长,若不等长,在短的字符串前补零,否则之后的操作会超出索引。
2)然后从后到前遍历所有的位数,同位相加,这里有一个点,用的是字符相加,利用 ASCII 码,字符在内部都用数字表示,我们不需要知道具体数值,但可知 ‘0’-‘0’ = 0, ‘0’+1=‘1’,以此类推 。字符的加减,大小比较,实际上都是内部数字的加减,大小比较
3)判断相加后的字符,若大于等于字符 ‘2’,下一位需要进一
4)第 0 位数的相加在这里是单独处理的,因为它可能涉及到字符的插入(即是否需要在最前面加一位数 ‘1’)
方法1:
class Solution {
public:
string addBinary(string a, string b) {
int al = a.size();
int bl = b.size();
while(al < bl) //让两个字符串等长,若不等长,在短的字符串前补零,否则之后的操作会超出索引
{
a = '0' + a;
++ al;
}
while(al > bl)
{
b = '0' + b;
++ bl;
}
for(int j = a.size() - 1; j > 0; -- j) //从后到前遍历所有的位数,除了0位,同位相加
{
a[j] = a[j] - '0' + b[j];
if(a[j] >= '2') //若大于等于字符‘2’,需要进一
{
a[j] = (a[j] - '0') % 2 + '0';
a[j-1] = a[j-1] + 1;
}
}
a[0] = a[0] - '0' + b[0]; //将ab的第0位相加
if(a[0] >= '2') //若大于等于2,需要进一
{
a[0] = (a[0] - '0') % 2 + '0';
a = '1' + a;
}
return a;
}
};
方法2:
class Solution {
public:
string addBinary(string a, string b) {
int a_iL=a.length(),b_iL=b.length();
int mi,ma;
string c;
string temp="0";
string _max;
if(a_iL>b_iL){mi=b_iL;ma=a_iL;_max=a;}
else {mi=a_iL;ma=b_iL;_max=b;}
for(int i=0;i<mi;i++){
if(temp=="0"){
if(a[a_iL-1-i]=='1' && b[b_iL-1-i]=='1'){temp="1";c='0'+c;}
else if(a[a_iL-1-i]=='1' || b[b_iL-1-i]=='1') c='1'+c;
else c='0'+c;
}
else if(temp=="1"){
if(a[a_iL-1-i]=='1' && b[b_iL-1-i]=='1'){c='1'+c;}
else if(a[a_iL-1-i]=='1' || b[b_iL-1-i]=='1'){c='0'+c;}
else{temp="0";c='1'+c;}
}
}
for(int i=mi;i<ma;i++){
if(temp=="0"){c=_max[ma-1-i]+c;}
if(temp=="1"){
if(_max[ma-1-i]=='1'){c='0'+c;}
else{temp="0";c='1'+c;}
}
}
if(temp=="1") c=temp+c;
return c;
}
};
28-实现strStr()
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
思路:基于滑动窗口
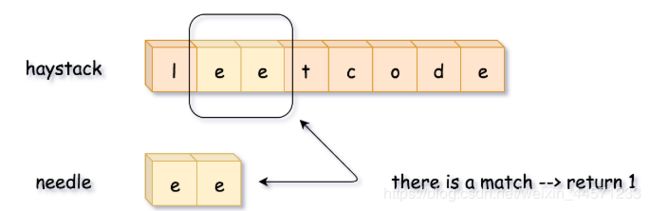
或者使用双指针:因为只有子串的第一个字符跟 needle 字符串第一个字符相同的时候才需要比较。
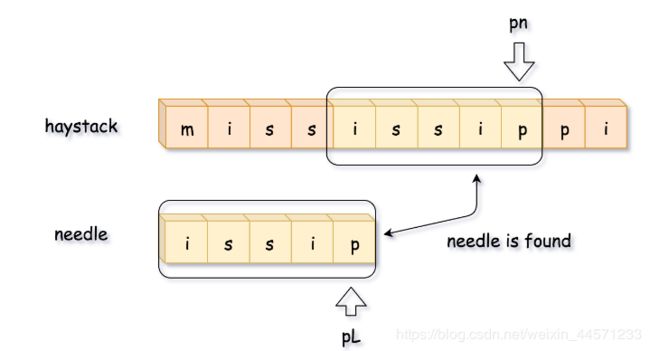
1)移动 pn 指针,直到 pn 所指向位置的字符与 needle 字符串第一个字符相等。
2)通过 pn,pL,curr_len 计算匹配长度。
3)如果完全匹配(即 curr_len == L),返回匹配子串的起始坐标(即 pn - L)。
4)如果不完全匹配,回溯。使 pn = pn - curr_len + 1, pL = 0, curr_len = 0。
错误提示:AddressSanitizer: heap-buffer-overflow on address
原因:数组访问越界,也是绝大部分内存问题
方法1代码:
class Solution {
public:
int strStr(string haystack, string needle) {
int sn=needle.size();
int sh=haystack.size();
if(sn==0) return 0;
if(sh<sn) return -1;
int sum=0;
for(int i=0;i<sh-sn+1;i++){
for(int j=0;j<sn;j++){
if(haystack[i+j]==needle[j]) ++sum;
}
if(sum==sn) return i;
else sum=0;
}
return -1;
}
};
14-最长公共前缀
示例 1:
输入: [“flower”,“flow”,“flight”] 输出: “fl”
示例 2:
输入: [“dog”,“racecar”,“car”] 输出: “”
解释: 输入不存在公共前缀。
注意:
1)特殊情况的判断,例如容器只有一个元素或者没有的情况
2)养成良好的编程习惯,去变量名称需要有区分度
思路:
1)首先,判断字符串数组只有一个元素和没有的情况
2)指针i指向每串字符的同一个位置的字符,指针j用来遍历每个字符串
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
int sum=0;
int min_size=0;
string out;
if(strs.size()==0) return out;
if(strs.size()==1) return strs[0];
for(int i=0;i<strs.size()-1;i++){
min_size=min(strs[i].size(),strs[i+1].size());}
for(int i = 0; i < min_size; i++) {
for(int j=0;j<strs.size()-1;j++) {
if (strs[0][i] == strs[j + 1][i]){++sum;}
else return out;
}
if (sum == strs.size()-1){out += strs[0][i];}
sum=0;
}
return out;
}
};
技巧:
双指针
情景1:
总之,使用双指针技巧的典型场景之一是你想要从两端向中间迭代数组。这时你可以使用双指针技巧:一个指针从始端开始,而另一个指针从末端开始。值得注意的是,这种技巧经常在排序数组中使用。
561-数组拆分
给定长度为 2n 的数组, 你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), …, (an, bn) ,使得从1 到 n 的 min(ai, bi) 总和最大。
思路:只需要排序之后,相邻之间组队就可以留下最大的
注意:变量初始化记得赋值,否则系统会给变量一个随机的初值
class Solution {
public:
int arrayPairSum(vector<int>& nums) {
int size=nums.size();
int sum=0;
sort(nums.begin(),nums.end());//用到了#include ,将数组升序排列
for(int i=0;i<size;i=i+2){
sum=sum+nums[i];
}
return sum;
}
};
167-两数之和
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
思路:
使用双指针,一个指针指向值较小的元素,一个指针指向值较大的元素。指向较小元素的指针从头向尾遍历,指向较大元素的指针从尾向头遍历。
如果两个指针指向元素的和 sum == target,那么得到要求的结果;
如果 sum > target,移动较大的元素,使 sum 变小一些;
如果 sum < target,移动较小的元素,使 sum 变大一些。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int low = 0, high = numbers.size() - 1;
while (low < high) {
int sum = numbers[low] + numbers[high];
if (sum == target)
return {low + 1, high + 1};
else if (sum < target)
++low;
else
--high;
}
return {-1, -1};
}
};
情景2:
这是你需要使用双指针技巧的一种非常常见的情况:
同时有一个慢指针和一个快指针。
解决这类问题的关键是
确定两个指针的移动策略。
与前一个场景类似,你有时可能需要在使用双指针技巧之前对数组进行排序,也可能需要运用贪心想法来决定你的运动策略。
485-最大连续1的个数
给定一个二进制数组, 计算其中最大连续1的个数。
示例 1:
输入: [1,1,0,1,1,1]
输出: 3
解释: 开头的两位和最后的三位都是连续1,所以最大连续1的个数是 3.
思路:
用一个计数器 count 记录 1 的数量,另一个计数器 maxCount 记录当前最大的 1 的数量。
当我们遇到 1 时,count 加一。
当我们遇到 0 时:
将 count 与 maxCount 比较,maxCoiunt 记录较大值。
将 count 设为 0。
返回 maxCount。
时间与空间复杂度都较高。
class Solution {
public:
int findMaxConsecutiveOnes(vector<int>& nums) {
int maxcount = 0, k = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] == 1) { ++k; }
else { maxcount=max(maxcount,k);k=0; }
}
maxcount=max(maxcount,k);
return maxcount;
}
};
209-长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
示例:
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
思路:基于滑动窗口
想象一下,在一个坐标上存在两个指针begin 和i ,begin 代表滑窗的左边框,i代表滑窗的右边框。两者通过分别向右滑动,前者能使窗口之间的和减小,后者能使窗口之间的和增大。开始时二者重合,窗口的和就是重合点所在的数。
1)开始i向右滑动,使和变大。
2)当恰好大于等于s时,记录滑窗所包括的子数组长度ans,若ans已有数值,需判断新值是否小于旧值,若是,更新ans。begin向右滑动
3)判断是否仍大于等于s
注意:在判断条件的选择时,由于判断为是,这里++i之后的i值是提供给下一次的计算使用,所以判断条件为sum+nums[i]
4)若是,重复步骤2,3。若否,转步骤1。直到右边框到达最右边
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int ans = INT_MAX;
int i = 0; //滑窗的右边框
int sum = 0; //窗口间的和
int begin = 0; //滑窗的左边框
while(i < nums.size()) //滑窗的右边框不能超出界限
{
if(sum + nums[i] < s) //若滑窗之间的和小于s,右边框右移,sum增大
//注意这里最后++i之后的i值是提供给下一次的计算使用,所以判断条件为sum+nums[i]
{
sum += nums[i];
++ i;
}
else //若滑窗之间的和大于等于s,左边框右移,sum减小
{
if(i - begin < ans) //若当前符合条件的连续子数组比ans内记录的长度更小,则更新ans值
ans = i - begin + 1;
sum = sum - nums[begin];
++ begin;
}
}
return ans == INT_MAX? 0:ans;
}
};
总结:
189-旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 :
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
思路1:
class Solution {
public:
void rotate(vector<int>& nums, int k) {
if(k>=nums.size()){k = k % nums.size();}
nums.insert(nums.begin(),nums.end()-k,nums.end());
nums.erase(nums.end()-k,nums.end());
}
};
思路2:
我们首先将所有元素反转。然后反转前 k 个元素,再反转后面 n−k 个元素,就能得到想要的结果。
原始数组 : 1 2 3 4 5 6 7
反转所有数字后 : 7 6 5 4 3 2 1
反转前 k 个数字后 : 5 6 7 4 3 2 1
反转后 n-k 个数字后 : 5 6 7 1 2 3 4 --> 结果
class Solution {
public:
void rotate(vector<int>& nums, int k) {
//采用反转
int length=size(nums);
k%=size(nums);
reverse(&nums[0],&nums[length]);//()中是喜爱嗯要反转的起始元素和最后一个元素+1(也就是超尾)
reverse(&nums[0],&nums[k]);//函数的头文件#include 119-杨辉三角2
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
示例:
输入: 3
输出: [1,3,3,1]
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> kRows(rowIndex+1);//第K行的vector大小为 rowIndex+1
for(int i = 0; i <= rowIndex; i++)//利用前一行求后一行,第K行要循环K遍
{
kRows[i] = 1;//行末尾为1
for(int j = i; j > 1; j--)//每一行的更新过程,每一行是从后往前更新
{
kRows[j-1] = kRows[j-2] + kRows[j-1];
}
}
return kRows;
}
};
151-翻转字符串里的单词
给定一个字符串,逐个翻转字符串中的每个单词。
输入: " hello world! "
输出: “world! hello”
解释: 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
无空格字符构成一个单词。
输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
思路:
1)先将字符串整体反转
2)确定子串的起始位置和结束位置
3)遍历这个单词,向前移动
4)单词局部反转
3)删除末尾多余的元素
class Solution {
public:
string reverseWords(string s) {
reverse(s.begin(),s.end());
int n=s.size();
int start=0,end=0,index=0;
for(;start<n;start++){
if(s[start] != ' '){
//除了首个单词,放一个空格作间隔
if(index != 0){s[index++]=' ';}
int end=start;
//替换原来的s直到空格
while(end<n && s[end]!= ' '){s[index++]=s[end++];}
//把每个单词的位置交换过来,此时单词长度为end-start,这里的index与end是循环之后+1的值
reverse(s.begin()+index-(end-start),s.begin()+index);
//更新下一个单词开始的地方
start=end;
}
}
//除去末尾的多余数据与空格
s.erase(s.begin()+index,s.end());
return s;
}
};
557-反转字符串中的单词3
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例 1:
输入: “Let’s take LeetCode contest”
输出: “s’teL ekat edoCteeL tsetnoc”
注意:在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格。
思路:
1)遍历字符串
2)在遍历中确定单词首尾,并反转单词
3)更新单词首尾
class Solution
{
public:
string reverseWords(string s)
{
//如果s是空字符串,直接返回
if (s.size() == 0){return s;}
int front = 0, back = 0;//front为要反转的单词的首字母,back为要反转的单词的末字母的下一位
for (int i = 0; i < s.size() ; i++)//
{
if (s[i] != ' '){back++;}
else{
reverse(s.begin() + front, s.begin() + back);
front = back + 1; //当前back指向空格,所以front要从空格的下一个即下一个单词的首字母开始
back = front;//front跟back同一线
}
} //此时最后一部分还没有反转,因为s的末尾不是空格,所以此时back应等于最后一个单词的末字母的下一个位置
reverse(s.begin() + front, s.begin() + back); //reverse的最后一个参数是要反转的结尾的下一位,back指向s的最后一位,所以要+1
return s;
}
};
26-删除排序
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 :
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
思路:快慢指针
1)遍历数组
2)找相同,是则赋值,不是就转到下一位
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n=nums.size();
int start=0,end=0;
if(nums.empty()) return 0;
for(;end<n;end++){
if(nums[start] != nums[end]){nums[++start]=nums[end];}
}
return start+1;
}
};
class Solution {
public:
int removeDuplicates(vector<int>& nums)
{
int length=0,n=0,size=nums.size();
if(size!=0){
vector<int>::iterator it=nums.begin(),rt=nums.begin();
it++;
length=1;
while(it!=nums.end())
{
if(*it==*rt){it++;}
else{
rt++;
*rt=*it;
length=length+1;
it++;
}
}
}
return length;
}
};
283-移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
思路:快慢指针
1)开始遍历快指针,判断慢指针是否为0;
2)为0则删除该处元素,并在队列尾部增加元素;
3)不为0则满指针右移;
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n=nums.size();
if(!nums.empty()){
int start=0;
for(int i=0;i<n;i++){
if(nums[start] == 0){
nums.emplace_back(0);
nums.erase(nums.begin()+start,nums.begin()+start+1);
}
else{start++;}
}
}
}
};
思路2:这里参考了快速排序的思想,快速排序首先要确定一个待分割的元素做中间点x,然后把所有小于等于x的元素放到x的左边,大于x的元素放到其右边。
这里我们可以用0当做这个中间点,把不等于0(注意题目没说不能有负数)的放到中间点的左边,等于0的放到其右边。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n=nums.size();
if(!nums.empty()){
int start=0;
for(int i=0;i<n;i++){
if(nums[i] != 0){
int temp = nums[i];
nums[i]=nums[start];
nums[start++]=temp;
}
}
}
}
};
3. 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
思路1:滑动窗口
class Solution
{
public:
int lengthOfLongestSubstring(string s)
{
//s[start,end) 前面包含 后面不包含
int start(0), end(0), length(0), result(0);
int sSize = int(s.size());
while (end < sSize)
{
char tmpChar = s[end];
for (int index = start; index < end; index++)
{
if (tmpChar == s[index])
{
start = index + 1;
length = end - start;
break;
}
}
end++;
length++;
result = max(result, length);
}
return result;
}
};
思路2:Hashmap
class Solution
{
public:
int lengthOfLongestSubstring(string s)
{
//s[start,end) 前面包含 后面不包含
int start(0), end(0), length(0), result(0);
int sSize = int(s.size());
unordered_map<char, int> hash;
while (end < sSize)
{
char tmpChar = s[end];
//仅当s[start,end) 中存在s[end]时更新start
if (hash.find(tmpChar) != hash.end() && hash[tmpChar] >= start)
{
start = hash[tmpChar] + 1;
length = end - start;
}
hash[tmpChar] = end;
end++;
length++;
result = max(result, length);
}
return result;
}
};
思路3:数组代替hashmap
class Solution
{
public:
int lengthOfLongestSubstring(string s)
{
//s[start,end) 前面包含 后面不包含
int start(0), end(0), length(0), result(0);
int sSize = int(s.size());
vector<int> vec(128, -1);
while (end < sSize)
{
char tmpChar = s[end];
//仅当s[start,end) 中存在s[end]时更新start
if (vec[int(tmpChar)] >= start)
{
start = vec[int(tmpChar)] + 1;
length = end - start;
}
vec[int(tmpChar)] = end;
end++;
length++;
result = max(result, length);
}
return result;
}
};
1451. 重新排列句子中的单词
「句子」是一个用空格分隔单词的字符串。给你一个满足下述格式的句子 text :句子的首字母大写、text 中的每个单词都用单个空格分隔。
请你重新排列 text 中的单词,使所有单词按其长度的升序排列。如果两个单词的长度相同,则保留其在原句子中的相对顺序。
请同样按上述格式返回新的句子。
示例 1:
输入:text = “Leetcode is cool”
输出:“Is cool leetcode”
解释:句子中共有 3 个单词,长度为 8 的 “Leetcode” ,长度为 2 的 “is” 以及长度为 4 的 “cool” 。
输出需要按单词的长度升序排列,新句子中的第一个单词首字母需要大写。
class Solution {
public:
string arrangeWords(string text) {
map<int, vector<string>> size2vec;//创建map,具有排序的键值对
int index = 0, t_len = text.size();
text[0] = text[0] - 'A' + 'a';
for(int i = 0; i <= t_len; i++) {
if(i == t_len || text[i] == ' ') {
int len = i - index;//计算每个单词长度
if(size2vec.find(len) == size2vec.end()) {//给未出现的长度的单词创建空间
size2vec[len] = vector<string>();
}
size2vec[len].push_back(text.substr(index, len));//进行对应单词长度的字符串的插入,同样长度的就直接插在后面
index = i + 1;//因为这时的i对应' ',所以需要跳过
}
}
string ans;
ans.reserve(t_len + 1);//设置ans的最小size
for(const auto& [key, str_val]: size2vec) {//按键取值
for(const string& s: str_val) {//遍历vector