深度神经网络模型压缩与加速研究综述

深度神经网络模型压缩与加速研究综述

---

前言

深度卷积神经网络(CNNs)近年来在许多视觉识别领域取得了巨大的成功。然而，现有的深度神经网络模型在计算上是昂贵的且内存是密集型的。这限制了他们在低配置的硬件上的运行。因此，在不显著降低模型性能的情况下，在深度网络中进行模型压缩和加速是一种自然的思路，在这篇博客里讲会大致的想你介绍这个领域内的技术，综述了近年来发展起来的压缩和加速CNNs模型的先进技术。这些技术大致分为四种方案。参数剪枝与共享（parameter pruning and sharing,）、低秩因子分解（ low-rank factorization）、传输/紧凑卷积滤波器（transferred/compact convolutional filters）和知识蒸馏（knowledge distillation）。 ，在接下来叙述中我会用英文描述这些单词，中文翻译过来总有种晦涩难懂的感觉，没有英文来的干脆。

介绍

近年来，深度神经网络得到了广泛的关注，在不同的应用领域得到了广泛的应用，并在许多任务中取得了显著的精度提高。这些工作依赖于具有数百万甚至数十亿参数的深度网络，而具有极高计算能力的gpu的可用性是这些工作成功的关键。 比为我就以为又没钱又想用到好的GPU而烦恼。一些网络的参数量可以达到数十亿个。

考虑到具有更多层和节点的更大的神经网络，减少它们的存储和计算成本变得至关重要，特别是对于一些实时应用，如在线学习和增量学习。此外，近年来在虚拟现实、增强现实和智能可穿戴设备方面取得了重大进展，为研究人员提供了前所未有的机会，以应对将深度学习系统部署到资源有限(如内存、CPU、能源、带宽)的便携设备的根本性挑战。高效的深度学习方法。例如，ResNet-50的50个卷积层需要超过95MB的内存来存储，处理一张图像需要超过38亿的浮点数乘法。在丢弃了一些冗余的权值之后，网络仍然可以正常工作，但是节省了更多75%的参数和50%的计算时间。对于像手机和fpga这样只有几兆内存的设备来说，如何压缩它们所使用的模型也很重要。

实现这些目标需要来自许多学科的联合解决方案，包括但不限于机器学习优化、计算机架构、数据压缩、索引和硬件设计。

• parameter pruning and sharing 探索了模型参数的冗余性，并尝试去除冗余性和非临界性。
• 基于Low-rank factorization的技术利用矩阵/张量分解来估计深层神经网络的信息参数。
• 基于transferred/compact convolutional filters方法设计了特殊结构的卷积滤波器，减少了参数空间，节省了存储/计算量。
• knowledge distillation知识精馏方法学习一个精馏模型并训练一个更紧凑的神经网络来重现一个更大的神经网络的输出

下面用一张表很好的总结这四种方法，也有提出四个方法的论文

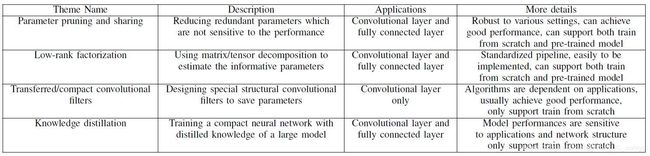
适用于具有全连接层和卷积层的DNN模型，具有可比较的性能

另一方面，

• 使用transferred/compact filters 的方法只适用于具有卷积层的模型。
• 基于Low-rank factorization and transfered/compact filters的方法提供了端到端的管道，可以在CPU/GPU环境中轻松实现，这很直接
• 而parameter pruning & sharing 则使用不同的方法，如矢量量化，二进制编码和稀疏约束来执行任务。

在训练协议方面，基于parameter pruning & sharing low-rank factorization的模型可以从预先训练的模型中提取，也可以从零开始训练。而transfered/compact filters和knowledge distillation模型只能支持从无到有的训练。

这些方法都是独立的研发出来的，但是他们之间的使用并没有互相的限制，你可以同时使用这四种方法里面的多种。

PARAMETER PRUNING AND SHARING

---

在早期时paramerter pruning and sharing 在减小模型的复杂度和处理模型过拟合的工作中取得了不错的效果。在这之后就有很多人来都研究paramerter pruning and sharing。现在这个技术大致被分成了3类

• quantization and binarization（量化和二值化）
• parameter sharing （参数共享）
• structural matrix （构造矩阵）

下面我们一个个来说

A. quantization and binarization

---

Network quantization（网络量化）通过减少表示每个权值所需的比特数来压缩原始网络。下面列出这方面相关研究的论文。

• 2014-Compressing Deep Convolutional Networks using Vector Quantization
  主要介绍了对参数值应用k-means标量量化所产生的效果，考虑参数的二值化，用k-means进行标量量化，用积量化或剩余量化进行结构化量化。
• 2015-Deep Learning with Limited Numerical Precision结果表明，在使用随机舍入时，深度网络只使用16位宽定点数表示就可以训练，分类精度几乎没有下降
• 2016-Deep Compression_ Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding中提出的方法利用权值共享对链路权值进行量化，然后对量化后的权值和Codebook进行霍夫曼编码，进一步降低了Codebook的速率，原理可以看下图
  
  它首先通过正常的网络训练来学习连接性，然后修剪小重量的连接。最后，对网络进行重新训练，以学习剩下的稀疏连接的最终权值。该工作在所有基于参数量化的方法中取得了最先进的性能
• 2017-TOWARDS THE LIMIT OF NETWORK QUANTIZATION中提到了可以使用Hessian权值来度量网络参数的重要性，并提出最小化分簇网络参数的平均Hessianweighted量化误差
• 在每个权值的1位表示的极端情况下，这就是二进制权值神经网络。有许多工作是直接训练CNNs与二进制权值的，如BinaryConnect ， BinaryNet和XNORNetworks。他们的主要目标都是在模型训练的过程中直接学习二进制权值或激活二进制权值。2016-Deep neural networks are robust to weight binarization and other non-linear distortions中表明，经过反向传播训练的网络能够抵抗特定的权值扭曲，包括二进制权值

缺点：
当处理像GoogleNet这样的大型cnn网络时，二进制网的精度会显著降低。这种二值化网络的另一个缺点是，现有的二值化方案基于简单的矩阵逼近，忽略了二值化对精度损失的影响。

• 2016-Loss-aware Binarization of Deep Networks这篇论文中提出了一种近端牛顿算法与对角海森近似的方法，相对于二进制权值直接最小化损失。

B. parameter sharingww

---

网络权值共享的方法以及被运用到了减小网络复杂度和解决网络过拟合的问题上。

早期的的思路有这些

• 基础的有偏置权重的衰减
• The Optimal Brain Damage and The Optimal Brain Surgeon 这种模型在Hessian损失函数的基础上减少了很多的连接数量。同时这样的剪枝方式比基于量级的剪枝，如权值衰减法的准确度要高很多

这些方法的训练程序遵循从无到有的训练方式。

在这个方向上，最近的一个趋势是在一个预先训练好的CNN模型中删除冗余的、非信息性的权重。

• 例如，Srinivas和Babu在2015-Data-free Parameter Pruning for Deep Neural Networks中探讨了神经元之间的冗余，并提出了一种无数据剪枝（data-free pruning）的方法来去除冗余神经元。
• 2015- Learning both Weights and Connections for EfficientNeural Networks中则提出减少整个网络中参数和操作的总数。

当然了相关的论文还有好多好多，我这里不一一列举了

缺点: 剪枝和分享可能有一些潜在的问题。

• 与一般方法相比，用l1或l2正则化进行剪枝需要更多的迭代来收敛
• 所有的修剪标准都需要为层手动设置灵敏度，这需要对参数进行微调，对于某些应用程序可能很麻烦。

C. structural matrix

---

在包含全连接层的架构中，探索全连接层中参数的冗余是非常有必要的。这往往是内存消耗的瓶颈. 一个m x n的矩阵可以用参数量小于mn 的矩阵去描述，用来描述的矩阵就叫做structural matrix（结构化矩阵）。该结构通过快速的矩阵向量乘法和梯度运算**，不仅降低了内存开销，而且大大加快了推理和训练的速度。**

• 沿着这个方向在论文Fast neural networks with circulant projections和An exploration of parameter redundancy in deep networks with circulant projections 提出了一种建立在循环检测基础上的一种简单有效的办法同时保持了不错的准确率。给你一个向量 r = (r0; r1; … ; rd-1) , 他对应的循环矩阵就这样给定义：
  
  这样memory cost 就从O（d^2) 变成了 O(d) ,循环结构矩阵同样可以使用FFT（Fast Fourier Transoform） 去提高计算的速度 给定d维向量r的情况下，Eq. 1中的上述1层循环神经网络的时间复杂度为O(d log d)。

• 在Deep fried convnets,” in International Conference on Computer Vision中提出了一种新的变换方法来重新参数化全连通层的矩阵向量乘法。 这篇论文提到的The Adapitive Fastfood 的转换矩阵被定义为：
  $$R=SHG\Pi HB$$
  S、G和B是任意的对角矩阵。Π ∈ $\{0,1{\}}^{d\times d}$ 是一个任意的置换矩阵。H表示Walsh-Hadamard矩阵，这种方法使用自适应方法对具有d个输入和n个输出的全连接层重新参数化从O(nd)到O(n)，从O(nd)到O(n log d)，分别减少了存储和计算成本。

缺点：

• 这类方法的一个问题是结构约束会影响性能，因为结构约束可能会给模型带来偏差。这也是模型压缩和加速的方法的一个通病了，想要获得速度的性能就必然会牺牲一些精度。
• 另一个问题就是想要找到合适的结构矩阵的很困难的，因为没有理论的方法可以让你直接找到他

LOW-RANK FACTORIZATION AND SPARSITY

---

在卷积神经网络中，卷积操作占据了大部分的运算，因此减少卷积层将会有助于改变模型的压缩率和提升模型的速度。 对于卷积核你可以把他看作一个4维的tensor。基于张量分解的思想是由四维张量中存在大量冗余的直觉得到的，这是一种特别有希望消除冗余的方法。对于全连通层，它可以被看作是一个2D矩阵，低秩性也有帮助。

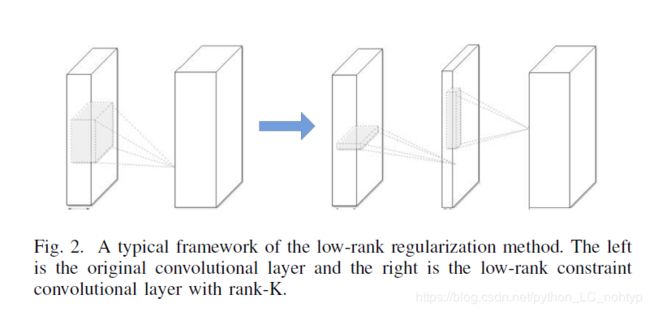
人们已经开始使用 low-rank filters去提升软件网络的精度很长时间了。例如DCT (discrete cosine transform)和wavelet系统分别用一维DCT变换和一维小波构造张量积。

• Rigamonti_Learning_Separable_Filters_2013_CVPR_paper中提出了Learning separable 1D filters
• Exploiting linear structure within convolutional networks for efficient evaluation针对一些简单的DNN模型，提出了几种低秩近似和聚类的卷积核算法。他们在一个卷积层上实现了2呗加速，分类准确率仅下降了1%。
• 2014-Speeding-up Convolutional Neural Networks Using Fine-tuned CP-Decomposition.pdf中提出了一种使用不同的张量分解方法，声称可以提高4.5倍的速度而精度只下降1%

The low-rank approximation 是逐层进行的。其中一层的参数确定后，根据重构误差准则对上述各层进行微调。 这些是典型的低秩压缩方法2D卷积层，在上图中已经描述了出来。

• 跟随着上述的思路，2014-Speeding-up Convolutional Neural Networks Using Fine-tuned CP-Decomposition中提出了核张量的正则并矢(CP)分解的方法。他们的工作是用非线性最小二乘法来计算CP分解。

• 在[40]中，提出了一种计算低秩张量分解的新算法，用于训练低秩约束的CNNs。利用批处理归一化(BN)对内部隐藏单元的激活进行转换。 一般来说，在[40] (BN)中CP和BN的分解方案都是一样的低级别)可以用来从零开始训练CNNs。然后，他们之间还是有微小的区别。例如，在CP分解中寻找最佳低秩近似是一个伪问题，最佳 rank-K (K是秩数)近似有时还可能不存在。而对于BN方案，分解总是存在的。我们对这两种方法进行了简单的比较，如下图所示。
  

The actual speedup and the compression ratess是用来衡量他们的性能的，如前所述，全连通层可以看作是一个二维矩阵，因此上述方法也可以应用于此。关于在全连通层中开发低秩性的经典作品有好几个。例如

• Misha在【2013-Predicting parameters in deep learning】 利用low-rank的方法减少了深层模型中动态参数的数量
• 【2013-Low-rank matrix factorization for deep neural network training with high-dimensional output targets】中探讨了DNN中final weigth layer的低秩矩阵分解方法，用于声学建模。

缺点：low-rank 对于模型压缩和加速是直接的，这一想法补充了最近在深度学习方面的进展，如dropout、矫正单元和maxout。 然而，实现并不容易，因为它涉及分解操作，这在计算上是昂贵的。另一个问题是，当前的方法是逐层执行低秩近似，因此不能执行全局参数压缩，这是很重要的，因为不同的层包含不同的信息。最后，与原始模型相比，因式分解需要大量的模型再训练来达到收敛性。

TRANSFERRED/COMPACT CONVOLUTIONAL FILTERS

---

CNNs是parameter efficient 的，这都要归功于它对输入图像的表示的平移不变性，而这点正是训练深层的网络模型不产生过分的过拟合所必须的。虽然目前缺乏一个强有力的理论，但大量的经验证据支持这样的观点，即平移不变性和卷积权值共享对良好的预测性能都很重要。使用TRANSFERRED CONVOLUTIONAL FILTERS来压缩CNN模型的想法是由[43]最近的工作所激发的，该工作引入了等变群理论（the equivariant group theory）。
让 $\mathrm{x}$作为输入, $\Phi (\cdot )$ 作为一个网络或者一个网络层 and $\mathcal{T}(\cdot )$ 作为transform matrix. 等价的概念被定义为:
$${\mathcal{T}}^{\prime }\Phi (\mathbf{x})=\Phi (\mathcal{T}\mathbf{x})$$
这表明通过：
indicating that transforming the input x by the transform $\mathcal{T}(\cdot )$ and then passing it through the network or layer $\Phi (\cdot )$ should give the same result as first mapping x through the network and then transforming the representation. （这句话不翻译了，翻译过来反而更难懂了） 变换$\mathcal{T}(\cdot )$和${\mathcal{T}}^{\prime }(\cdot )$不一定是相同的，因为它们作用于不同的对象。根据这个理论，根据这一理论,合理应用变换层或flters Φ(·)压缩整个网络模型。从实证观察中我们可以发现 deep CNNs 同样受益于使用作为模型的正则化器的使用一组很小的基频的特定的变换$\mathcal{T}(\cdot )$。
按照这个方向，最近有许多研究建议从一组基本filter构建一个卷积层

• 【Group equivariant convolutional networks】
• 【Doubly convolutional neural networks】
• 【Understanding and improving convolutional neural networks via concatenated rectifed linear units】
• 【Multi-bias non-linear activation in deep neural networks】

它们的共同点是，变换T(·)属于只在卷积flter的空间域内操作的一类函数，例如在【Understanding and improving convolutional neural networks via concatenated rectifed linear units】中的工作发现CNNs的下卷积层通过学习冗余flters来提取输入信号的正负相位信息，将T(·)定义为简单的否定函数:
$$\mathcal{T}\left({\mathbf{W}}_x\right)={\mathbf{W}}_x^{-}$$

这里${\mathbf{W}}_x$是基础的卷积核，${\mathbf{W}}_x^{-}$是由激活与Wx相反的 shift 组成的flter x，这些shilt 是在max-pooling操作后选择的。通过这个操作可以简单的实现在所有的卷积层上都有2倍的压缩率。结果表明，否定变换是一种强正则化方法，提高了分类精度。直观的理解是，使用pair-wise positive-negative constraint的学习算法可以得到有用的卷积filter，而不是冗余的filter。

在【Multi-bias non-linear activation in deep neural networks】中发现，卷积核的响应幅度在网络中具有广泛的模式表示多样性，仅用一个阈值来舍弃较弱的信号是不合适的. 为此，提出了一种多偏置非线性激活函数，以较低的计算代价在特征空间中生成更多的模式,转换$\mathcal{T}(\cdot )$被定义为：

$${\mathcal{T}}^{\prime }\Phi (\mathbf{x})={\mathbf{W}}_x+\delta$$
$\delta$是multi-bias 特征。在【Understanding and improving convolutional neural networks via concatenated rectifed linear units】中考虑一个多90◦和水平/垂直配置的旋转组合:

$${\mathcal{T}}^{\ast }\Phi (\mathbf{x})={\mathbf{W}}^{T_{\theta }}$$

where ${\mathbf{W}}^{T_{\theta }}$ was the transformation matrix which rotated the original filters with angle $\theta \in \{90,180,270\}.$ 在【Group equivariant convolutional networks】中变换推广到任何从数据中获取到的角度数据,θ也是直接从数据获得。

在【Doubly convolutional neural networks】中定义$\mathcal{T}(\cdot )$作为应用在2D filters上的translation function。
$${\mathcal{T}}^{‘}\Phi (\mathbf{x})=T(\cdot ,x,y{)}_{x,y\in \{-k,\dots ,k\},(x,y)\ne (0,0)}$$

$T(\cdot ,x,y)$表示将第一个操作数沿其空间维数(x, y)平移，并在边界上加上适当的补零以保持形状。提出的框架可用于$\mathbf{R}=\mathrm{circ}(\mathbf{r}):=\left[\begin{array}{ccccc}{r}_0& r_{d-1}& \dots & r_2& r_1\\ r_1& r_0& r_{d-1}& & r_2\\ ⋮& r_1& r_0& \ddots & ⋮\\ r_{d-2}& & \ddots & \ddots & r_{d-1}\\ r_{d-1}& r_{d-2}& \dots & r_1& r_0\end{array}\right]$改善分类精度的问题作为maxout网络的正则化版本，帮助$\mathbf{R}=\mathbf{S}\mathbf{H}\mathbf{G}\mathbf{I}\mathbf{I}\mathbf{H}\mathbf{B}$通过灵活地改变它们的体系结构来压缩网络来实现参数效率。

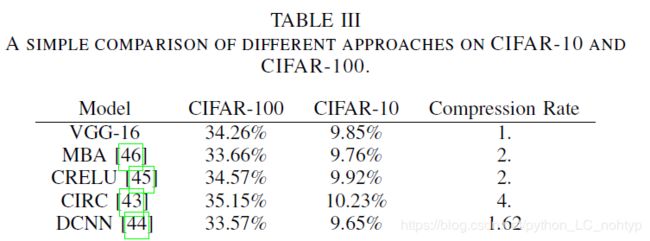
TABLE Ⅲ 中简要的概述了transferred convolutional filter在使用VGGNet作为基本框架不同的网络模型取得的效果。结果表明，它们可以在分类精度几乎没有下降的情况下实现参数的减少。

缺点: 对于将transform constraints to couvolutional filter的方法，需要解决的问题很少.

• 首先，这些方法可以在宽/胖的架构(如VGGNet)上获得有竞争力的性能，而在窄/深的架构(如GoogleNet、残余网)上却没有竞争力。其次，迁移假设有时过于强大，无法指导学习，导致结果在某些情况下不稳定。
• 使用紧凑的filter进行卷积可以直接降低计算成本。关键的想法是用紧凑的块代替松散的和过度参数化的filters来提高速度，这将显著地加速CNNs在几个基准上的运行。

KNOWLEDGE DISTILLATION(知识蒸馏)

---

据我们所知，Caruana等人首先提出利用知识转移(KT)来压缩模型。他们训练了一个带有伪数据标记的强分类器的压缩/集成模型，并复制了原始大网络的输出，但这项工作仅限于浅层模型。该思想最近被论文【Do deep nets really need to be deep?】采用作为知识蒸馏(KD)，将深度和广度的网络压缩为较浅的网络，其中压缩模型模仿复杂模型学习的功能。KD方法的主要思想是通过softmax学习课堂分布输出，将知识从大型teacher model转化为小型teacher model

【Distilling the knowledge in a neural network】的工作引入了KD压缩框架，该框架通过遵循学生-教师的范式简化了深层网络的训练，在这种范式中，学生根据教师输出的软化版本受到”惩罚“。该框架将一个教师网络集合压缩成一个具有类似深度的学生网络。学生被训练去预测输出和分类标签。尽管KD算法简单，但它在各种图像分类任务中显示出了良好的效果。听起来是不是很像自编码器呢？

【Fitnets: Hints for thin deep nets】中的工作旨在利用深度神经网络来解决网络压缩问题，它提出了一种训练细而深的网络的方法，称为FitNets，来压缩宽而浅的(但仍然深的)网络。该方法扩展了该思想，允许更薄和更深的学生模型。为了学习教师网络的中间表示，FitNet让学生模仿教师的全部特征图。然而，这样的假设过于严格，因为教师和学生的能力可能会有很大的不同。以上方法均在MNIST、CIFAR10、CIFAR-100、SVHN和AFLW基准数据集上得到验证同时这些方法能较好地匹配或优于教师的教学效果，但所需的参数和乘法明显减少。

沿着这个方向有几个延伸的蒸馏知识。

-【Bayesian dark knowledge】中的工作训练了一个参数化的学生模型来近似蒙特卡罗老师。该框架采用在线训练，学生模型采用深度神经网络。

• 与以往用软化标记概率表示知识的工作不同，【Face model compression by distilling knowledge from neurons】利用隐藏层的神经元来表示知识，该隐藏层保留的信息与标签概率相同，但更紧凑。
• 【Net2net: Accelerating learning via knowledge transfer】的工作通过瞬间将知识从以前的网络转移到每个更深或更广的新网络，加速了实验过程。这些技术是基于神经网络之间的功能保持转换的概念
• Zagoruyko等人【Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer】提出了注意转移(AT)放松FitNet的假设。他们转移了注意力地图，那是全部激活的总结。

缺点：
基于KD的方法可以使模型的深度更小，大大降低计算成本，然而，也有一些缺点。

• KD只能应用于具有softmax损失函数的分类任务，这阻碍了它的使用
• 模型假设有时过于严格，使得性能无法与其他类型的方法竞争
  

讨论与挑战

---

深度模型的压缩和加速技术还处在早期阶段，目前还存在以下挑战：

• 大多数目前的顶尖方法都建立在设计完善的 CNN 模型的基础上，这限制了改变配置的自由度（例如，网络结构和超参数）。为了处理更加复杂的任务，还需要更加可靠的模型压缩方法。
• 剪枝是一种压缩和加速 CNN 的有效方式。目前大多数的剪枝技术都是以减少神经元之间的连接设计的。另一方面，对通道进行剪枝可以直接减小特征映射的宽度并压缩模型。这很有效，但也存在挑战，因为减少通道会显著地改变下一层的输入。确定这类问题的解决方式同样很重要。
• 正如之前所提到的，结构化矩阵和迁移卷积滤波器方法必须使模型具有人类先验知识，这对模型的性能和稳定性有显著的影响。研究如何控制强加先验知识的影响是很重要的。
• 知识精炼（knowledge distillation/KD）方法有很多益处比如不需要特定的硬件或实现就能直接加速模型。开发基于 KD 的方法并探索如何提升性能仍然值得一试。
• 多种小型平台（例如，移动设备、机器人、自动驾驶汽车）的硬件限制仍然是阻碍深层 CNN 扩展的主要问题。如何全面利用有限的可用计算资源以及如何为这些平台设计特定的压缩方法仍然是个挑战。

到这里最经典的四种神经网络模型压缩与加速的方法总算介绍完了，陆陆续续写了三个星期，喜欢的请给赞鼓励一下哈。