神经网络＆DNN算法原理及代码实现（更新中）

本文整理了神经网络＆DNN算法原理及代码实现，主要参考了吴恩达老师的深度学习课程以及课程作业，适合中级学习人员做参考资料查阅

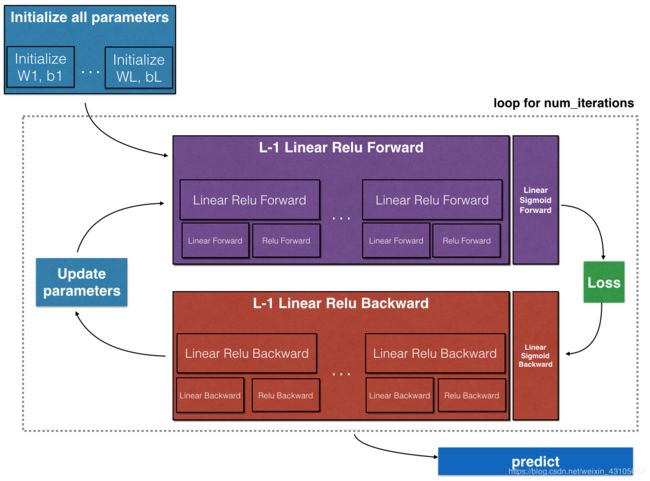
1.Normalizing inputs（归一化/标准化输入）
the weight matrices $(W^{[1]},W^{[2]},W^{[3]},...,W^{[L-1]},W^{[L]})$，the bias vectors $(b^{[1]},b^{[2]},b^{[3]},...,b^{[L-1]},b^{[L]})$

• min-max标准化

$x^{\prime }=\frac{x-\min (x)}{\max (x)-\min (x)}$

def min_max_normalization(X):
        X = float(X - np.min(X))/(np.max(X)- np.min(X))
        return X

• Z-score标准化

$x^{\ast }=\frac{x-\mu }{\sigma }$

def min_max_normalization(X):
    X = float(X - np.min(X))/(np.max(X)- np.min(X))
    return X

2. Initialize_parameters（初始化参数W, b）

• Zero initialization

W, b = np.zeros((…, …))

def initialize_parameters_zeros(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    parameters = {}
    L = len(layers_dims)            # number of layers in the network
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.zeros((layers_dims[l],layers_dims[l-1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
    return parameters

• Random initialization

W,b = np.random.randn((…, …))*10

def initialize_parameters_random(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    parameters = {}
    L = len(layers_dims)            # integer representing the number of layers
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*10
        parameters['b' + str(l)] = np.zeros((layers_dims[l],1))

    return parameters

• He initialization

$w^{[l]}=np.$ random. randn (shape) * np. sqrt$\left(\frac{2}{n^{[l-1]}}\right)$

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers
    
    for l in range(1, L + 1):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*np.sqrt(2./layers_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l],1))

    return parameters

3. Activation function（激活函数）

• sigmoid function

$sigmoid(z)=\frac{1}{1+e^{-z}}$

def sigmoid(Z):
    """
    Implements the sigmoid activation in numpy
    
    Arguments:
    Z -- numpy array of any shape
    
    Returns:
    A -- output of sigmoid(z), same shape as Z
    cache -- returns Z as well, useful during backpropagation
    """
    A = 1/(1+np.exp(-Z))
    cache_Z = Z
    
    return A, cache_Z

• sigmoid backward function

$sigmoid\_derivative(z)={\sigma }^{\prime }(z)=\sigma (z)(1-\sigma (z))$

def sigmoid_backward(dA, cache):
    """
    Implement the backward propagation for a single SIGMOID unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    
    Z = cache
    s, cache_Z= sigmoid(Z)
    dZ = dA * s * (1-s)
    
    return dZ

• relu function

$g(z)=\max (0,z)$

def relu(Z):
    """
    Implement the RELU function.

    Arguments:
    Z -- Output of the linear layer, of any shape

    Returns:
    A -- Post-activation parameter, of the same shape as Z
    cache -- a python dictionary containing "A" ; stored for computing the backward pass efficiently
    """
    
    A = np.maximum(0,Z)
    cache_Z = Z 
    return A, cache_Z

• relu backward function

$g(z{)}^{\prime }=\{\begin{array}{ll}0& \text{ if }z<0\\ 1& \text{ if }z>0\\ undefined& \text{ if }z=0\end{array}$

def relu_backward(dA, cache):
    """
    Implement the backward propagation for a single RELU unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    
    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.
    
    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0
    
    return dZ

4. Forward propagation（正向传播）

• activation function

$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$

def linear_forward(A, W, b):
    """
    Implement the linear part of a layer's forward propagation.

    Arguments:
    A -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)

    Returns:
    Z -- the input of the activation function, also called pre-activation parameter 
    cache -- a python dictionary containing "A", "W" and "b" ; stored for computing the backward pass efficiently
    """
    
    Z = W.dot(A) + b
    cache_AWb = (A, W, b)
    
    return Z, cache_AWb

def linear_activation_forward(A_prev, W, b, activation):
    """
    Implement the forward propagation for the LINEAR->ACTIVATION layer

    Arguments:
    A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    A -- the output of the activation function, also called the post-activation value 
    cache -- a python dictionary containing "linear_cache" and "activation_cache";
            stored for computing the backward pass efficiently
    """
    
    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache_AWb = linear_forward(A_prev, W, b)
        A, activation_cache_Z = sigmoid(Z)
    
    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache_AWb = linear_forward(A_prev, W, b)
        A, activation_cache_Z = relu(Z)
    
    cache_AWbZ = (linear_cache_AWb, activation_cache_Z)

    '''cache_AWbZ = ((Al-1, Wl, bl), Zl)'''
    return A, cache_AWbZ  

• L_model_forward

$A^{[l]}=g(Z^{[l]})=g(W^{[l]}{A}^{[l-1]}+b^{[l]})$

def L_model_forward(X, parameters):
    """
    Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
    
    Arguments:
    X -- data, numpy array of shape (input size, number of examples)
    parameters -- output of initialize_parameters_deep()
    
    Returns:
    AL -- last post-activation value
    caches -- list of caches containing:
                every cache of linear_relu_forward() (there are L-1 of them, indexed from 0 to L-2)
                the cache of linear_sigmoid_forward() (there is one, indexed L-1)
    """

    caches = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network
    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    for l in range(1, L):
        A_prev = A 
        '''cache_AWbZ = ((Al-1, Wl, bl), Zl)'''
        A, cache_AWbZ = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")
        '''caches = [ ((A0/X, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-2, WL-1, bL-1), ZL-1) ]'''  
        caches.append(cache_AWbZ)
    
    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    '''cache_AWbZ = ((Al-1, Wl, bl), Zl)'''
    AL, cache_AWbZ = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid") 
    '''caches = [ ((A0/X, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-1, WL, bL), ZL)  ]'''
    caches.append(cache_AWbZ) 

    '''caches = [ ((A0/X, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-1, WL, bL), ZL)  ]'''        
    return AL, caches  

• Forward propagation with dropout

---

def L_model_forward_with_dropout(X, parameters, keep_prob = 0.5):
    """
    Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
    
    Arguments:
    X -- input dataset, of shape (2, number of examples)
    parameters -- python dictionary containing your parameters "W", "b"
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    AL -- last activation value, output of the forward propagation
    cache -- tuple, information stored for computing the backward propagation
    """

    caches = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network

    # [LINEAR -> RELU]  ×  (L-1) -> LINEAR -> SIGMOID backward (whole model)
    for l in range(1, L):
        A_prev = A
        D = np.random.rand(A.shape[0],A.shape[1])               # Step 1: initialize matrix D1 = np.random.rand(..., ...)
        D = D < keep_prob                                       # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
        A_prev = A_prev * D                                    # Step 3: shut down some neurons of A1
        A_prev = A_prev / keep_prob                             # Step 4: scale the value of neurons that haven't been shut down
        '''cache_AWbZ = ((A, W, b), Z)'''
        A, cache_AWbZ = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")  
        '''caches = [ ((A1, W1, b1), Z1),  ((A2, W2, b2), Z2),  ......, ((AL-1, WL-1, bL-1), ZL-1) ]'''
        caches.append(cache_AWbZ)  

    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    '''cache_AWbZ = ((A, W, b), Z)'''
    AL, cache_AWbZ = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")  
    '''caches = [ ((A1, W1, b1), Z1),  ((A2, W2, b2), Z2),  ......, ((AL, WL, bL), ZL)  ]'''
    caches.append(cache_AWbZ)  

    '''caches = [ ((A1, W1, b1), Z1),  ((A2, W2, b2), Z2),  ......, ((AL, WL, bL), ZL)  ]'''
    return AL, cache 

5. Cost function（代价函数）

• compute cost

$$J=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log \left(a^{[L](i)}\right)+(1-y^{(i)})\log \left(1-a^{[L](i)}\right))$$

def compute_cost(AL, Y):
    """
    Implement the cost function defined by equation (7).

    Arguments:
    AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
    Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)

    Returns:
    cost -- cross-entropy cost
    """
    
    m = Y.shape[1]

    # Compute loss from aL and y.
    cost = -1 / m * np.sum(Y * np.log(AL) + (1-Y) * np.log(1-AL),axis=1,keepdims=True)
    cost = np.squeeze(cost)      # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).

    return cost

• compute cost with regularization

$$J_{regularized}=\underset{\text{cross-entropy cost}}{-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log \left(a^{[L](i)}\right)+(1-y^{(i)})\log \left(1-a^{[L](i)}\right))}+\underset{\text{L2 regularization cost}}{\frac{1}{m}\frac{\lambda }{2}\sum _l\sum _k\sum _j{W}_{k,j}^{[l]2}}$$

def compute_cost_with_regularization(AL, Y, parameters, lambd):
    """
    Implement the cost function with L2 regularization. See formula (2) above.
    
    Arguments:
    A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    parameters -- python dictionary containing parameters of the model
    
    Returns:
    cost - value of the regularized loss function (formula (2))
    """
    m = Y.shape[1]
    L = len(parameters)//2
    
    cross_entropy_cost = compute_cost(AL, Y) # This gives you the cross-entropy part of the cost
    
    L2_regularization_cost = 0
    for l in range(1, L):
        L2_regularization_cost += np.sum(np.square(parameters['W' + str(l)]))
    cost = cross_entropy_cost + (1./m*lambd/2)*(L2_regularization_cost)
    
    return cost

6. Backward propagation（反向传播）

• linear backward function with regularization

$$d{W}^{[l]}=\frac{\partial \mathcal{L}}{\partial W^{[l]}}=\frac{1}{m}d{Z}^{[l]}{A}^{[l-1]T}+\frac{\lambda }{m}\ast W^{[l]}$$ $$d{b}^{[l]}=\frac{\partial \mathcal{L}}{\partial b^{[l]}}=\frac{1}{m}\sum _{i=1}^{m}d{Z}^{[l](i)}$$ $$d{A}^{[l-1]}=\frac{\partial \mathcal{L}}{\partial A^{[l-1]}}=W^{[l]T}d{Z}^{[l]}$$

def linear_backward(dZ, linear_cache, lambd):
    """
    Implement the linear portion of backward propagation for a single layer (layer l)

    Arguments:
    dZ -- Gradient of the cost with respect to the linear output (of current layer l)
    linear_cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer
            '''linear_cache = (AL, WL, bL)'''

    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    A_prev, W, b = linear_cache
    m = A_prev.shape[1]

    dW = 1./m * np.dot(dZ, A_prev.T) + lambd/m * W
    db = 1./m * np.sum(dZ, axis=1, keepdims = True)
    dA_prev = np.dot(W.T, dZ)

    return dA_prev, dW, db


def linear_activation_backward(dA, cache, lambd, activation):
    """
    Implement the backward propagation for the LINEAR->ACTIVATION layer.
    
    Arguments:
    dA -- post-activation gradient for current layer l 
    cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
            '''current_cache = ((AL, WL, bL), ZL)'''
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
    
    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW -- Gradient of the cost with respect to W (current layer l), same shape as W
    db -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    linear_cache, activation_cache = cache
    '''linear_cache = (Al-1, Wl, bl), activation_cache= Zl '''
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache, lambd)
        
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache, lambd)
    
    return dA_prev, dW, db

backward propagation with regularization

def L_model_backward_with_regularization(AL, Y, caches, lambd):
    """
    Implements the backward propagation of our baseline model to which we added an L2 regularization.

    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    caches -- list of caches containing:
                '''caches = [ ((A0/X, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-1, WL, bL), ZL)  ]'''
                every cache of linear_activation_forward() with "relu" (there are (L-1) or them, indexes from 0 to L-2)
                the cache of linear_activation_forward() with "sigmoid" (there is one, index L-1)
    lambd -- regularization hyperparameter, scalar

    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL

    # Initializing the backpropagation
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
    '''current_cache = ((AL-1, WL, bL), ZL)'''
    current_cache = caches[L-1]
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, lambd, activation = "sigmoid")
    for l in reversed(range(L-1)):
        ''' l = L-2, L-3, ...., 2, 1, 0 '''
        # lth layer: (RELU -> LINEAR) gradients.
        '''current_cache = (AL-2, WL-1, bL-1), ZL-1)'''
        current_cache = caches[l] 
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, lambd, activation = "relu")
        grads["dA" + str(l + 1)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp

    return grads

6. Update parameters（更新参数）

• update_parameters function

$$W^{[l]}=W^{[l]}-\alpha d{W}^{[l]}$$ $$b^{[l]}=b^{[l]}-\alpha d{b}^{[l]}$$

def update_parameters(parameters, grads, learning_rate):
    """
    Update parameters using gradient descent
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    grads -- python dictionary containing your gradients, output of L_model_backward
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
                parameters["W" + str(l)] = ... 
                parameters["b" + str(l)] = ...
    """
    
    L = len(parameters) // 2 # number of layers in the neural network

    # Update rule for each parameter. Use a for loop.
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
        
    return parameters

7. predict（预测结果）

def predict(X, y, parameters):
    """
    This function is used to predict the results of a  L-layer neural network.
    
    Arguments:
    X -- data set of examples you would like to label
    parameters -- parameters of the trained model
    
    Returns:
    p -- predictions for the given dataset X
    """
    
    m = X.shape[1]
    n = len(parameters) // 2 # number of layers in the neural network
    p = np.zeros((1,m))
    
    # Forward propagation
    probas, caches = L_model_forward(X, parameters)

    
    # convert probas to 0/1 predictions
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0
    print("Accuracy: "  + str(np.sum((p == y)/m)))
        
    return p

8.DNN

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 300, lambd = 0, print_cost=False, keep_prob = 0.5):#lr was 0.009
    """
    Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
    
    Arguments:
    X -- data, numpy array of shape (number of examples, num_px * num_px * 3)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
    learning_rate -- learning rate of the gradient descent update rule
    num_iterations -- number of iterations of the optimization loop
    print_cost -- if True, it prints the cost every 100 steps
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """
    costs = []                         # keep track of cost
    
    # Parameters initialization.
    parameters = initialize_parameters_random(layers_dims)
    
    # Loop (gradient descent)
    for i in range(0, num_iterations):

        # Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
        '''caches = [ ((A0, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-1, WL, bL), ZL)  ]'''
        AL, caches = L_model_forward(X, parameters)
        '''caches = [ ((A0, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-1, WL, bL), ZL)  ]'''  
        # AL, caches = L_model_forward_with_dropout(X, parameters, keep_prob = 0.5)   
        
        # Compute cost.
        # cost = compute_cost(AL, Y)
        cost = compute_cost_with_regularization(AL, Y, parameters, lambd)
    
        # Backward propagation.
        '''caches = [ ((A0, W1, b1), Z1),  ((A1, W2, b2), Z2),  ......, ((AL-1, WL, bL), ZL)  ]'''
        grads = L_model_backward_with_regularization(AL, Y, caches, lambd)

        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)
                
        # Print the cost every 100 training example
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)
            
    # plot the cost
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters