树

---

有许多逻辑关系并不是简单的线性关系，在实际场景中，常常存在着一对多，甚至是多对多的情况，其中树就是典型的非线性数据结构。

---

什么是树

什么是树呢？在现实生活中有很多体现树的逻辑的例子。如企业里的职级关系，也是一个“树”。

这些树有共同的特点，从同一个“根”衍生出许多“枝干”，再从每一个“枝干”衍生出许多更小的“枝干”，最后衍生出更多的“叶子”。

在数据结构中，树的定义如下。

树（tree）是n（n≥0）个节点的有限集。当n=0时，称为空树。在任意一个非空树
中，有如下特点。

1：有且仅有一个特定的称为根的节点。

2：当n>1时，其余节点可分为m（m>0）个互不相交的有限集，每一个集合本身又是一个树，并称为根的子树。

在上图中，节点1是根节点（root）；节点5、6、7、8、9是树的末端，没有“孩子”，被称为叶子节点（leaf）。图中的虚线部分，是根节点1的其中一个子树。

同时，树的结构从根节点到叶子节点，分为不同的层级。从一个节点的角度来看，它的上下级和同级节点关系如下。

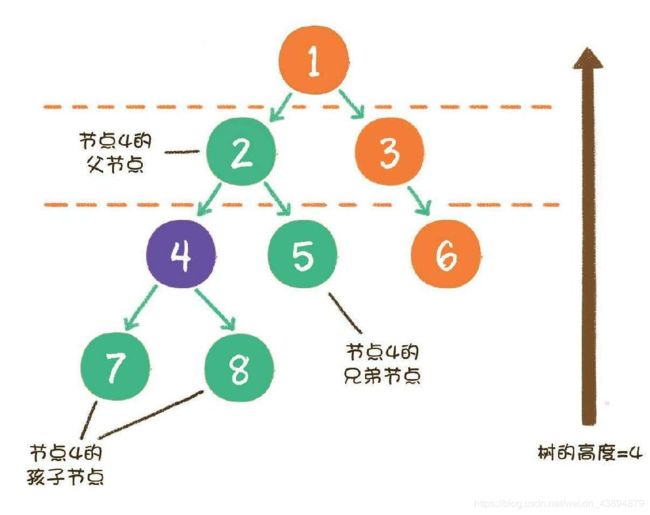
在上图中，节点4的上一级节点，是节点4的父节点（parent）；从节点4衍生出来的节点，是节点4的孩子节点（child）；和节点4同级，由同一个父节点衍生出来的节点，是节点4的兄弟节点（sibling）。
树的最大层级数，被称为树的高度或深度。显然，上图这个树的高度是4。

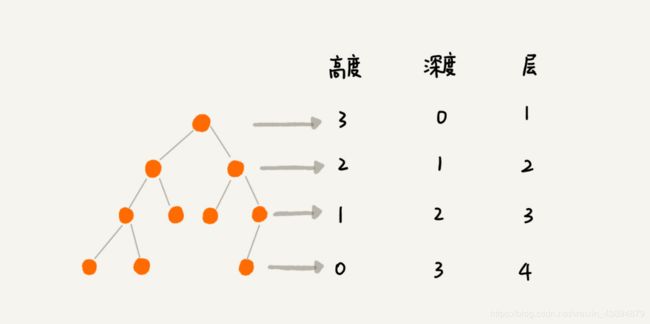
关于树有三个相似的概念：高度（Height）、深度（Depth）、层（Level）。它们的定义是这样的：

这三个概念的定义比较容易混淆，描述起来也比较空洞。举个例子说明一下，一看应该就能明白。

---

二叉树

二叉树（binary tree）是树的一种特殊形式。二叉，顾名思义，这种树的每个节点最多有2个孩子节点。注意，这里是最多有2个，也可能只有1个，或者没有孩子节点。

二叉树节点的两个孩子节点，一个被称为左孩子（left child），一个被称为右孩子（right child）。

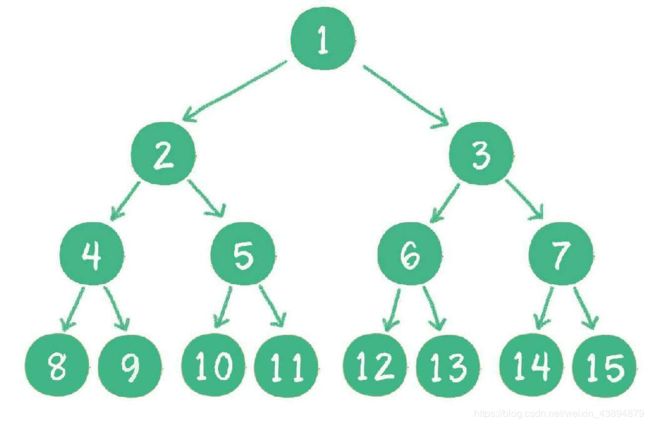
满二叉树

一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

完全二叉树

对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n。如果这
个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树。

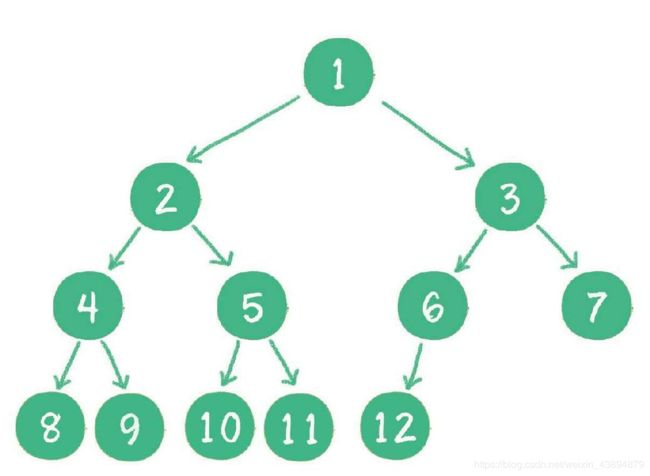
完全二叉树的条件没有满二叉树那么苛刻：满二叉树要求所有分支都是满的；而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

二叉树存储结构

1： 链式存储结构。

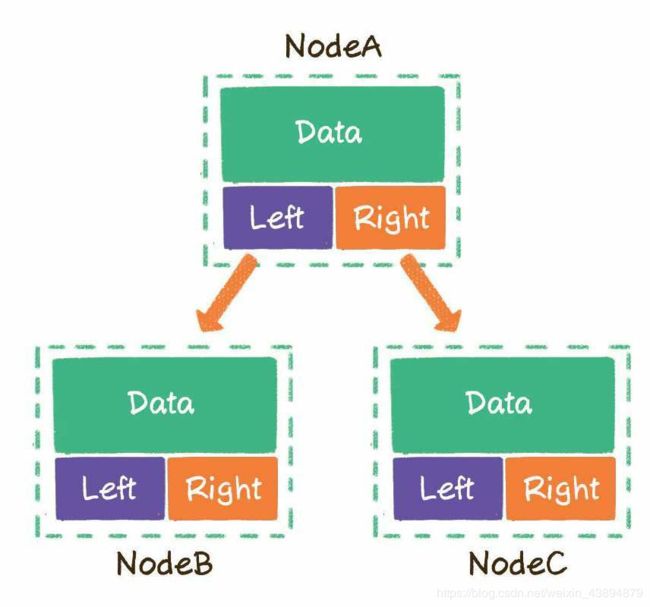
二叉树的每一个节点包含3部分。
存储数据的data变量
指向左孩子的left指针
指向右孩子的right指针

2： 数组。

如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点。使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。

---

二叉树的应用

查找

二叉查找树（binary search tree）。光看名字就可以知道，这种二叉树的主要作用就是进行查找操作。

二叉查找树在二叉树的基础上添加了以下几个条件。
1：如果左子树不为空，则左子树上所有节点的值均小于根节点的值
2：如果右子树不为空，则右子树上所有节点的值均大于根节点的值
3：左、右子树也都是二叉查找树

增加这些条件可以使查找更加方便

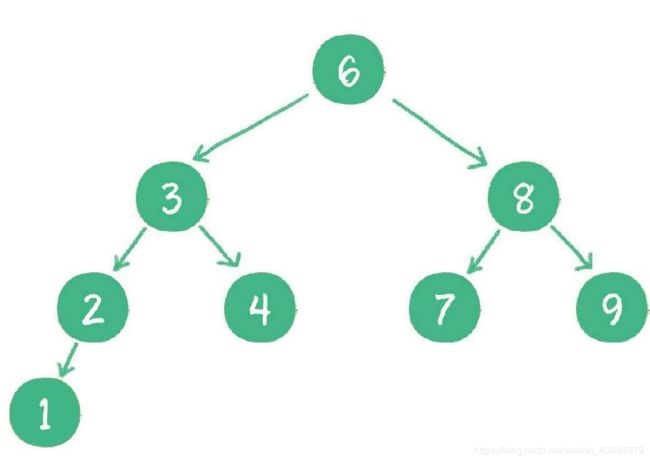
对于一个节点分布相对均衡的二叉查找树来说，如果节点总数是n，那么搜索节点的
时间复杂度就是O(logn)，和树的深度是一样的。这种依靠比较大小来逐步查找的方式，和二分查找算法非常相似。

使用链表实现二叉查找树：二叉查找树代码实现

维持相对顺序

二叉查找树要求左子树小于父节点，右子树大于父节点，正是这样保证了二叉树的有序性。因此二叉查找树还有另一个名字——二叉排序树（binary sort tree）。新插入的节点，同样要遵循二叉排序树的原则。

例如插入新元素5，由于5<6，5>3，5>4，所以5最终会插入到节点4的右孩子位置。

这一切看起来很顺利，然而却隐藏着一个致命的问题。什么问题呢？下面请试着在二叉查找树中依次插入9、8、7、6、5、4，看看会出现什么结果。

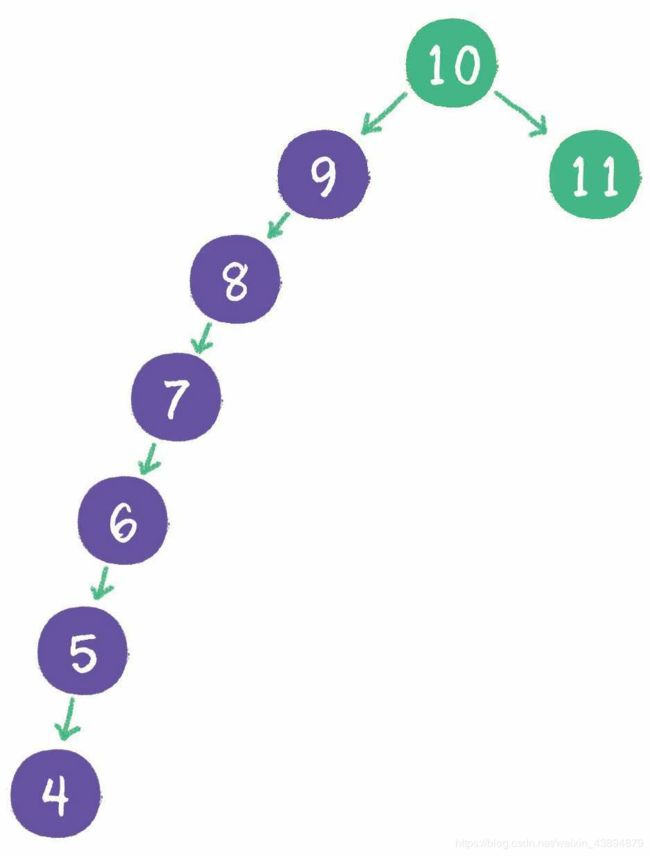
这种情况出现之后，查询节点的时间复杂度也退化成了O(n)。怎么解决这个问题呢？这就涉及二叉树的自平衡了。二叉树自平衡的方式有多种，如红黑树、AVL树、树堆等。

---

二叉树的遍历

从节点之间位置关系的角度来看，二叉树的遍历分为四种。
1：前序遍历
2：中序遍历
3：后序遍历
4：层序遍历

从更宏观的角度来看，二叉树的遍历归结为两大类。
1：深度优先遍历（前序遍历、中序遍历、后序遍历）
2：广度优先遍历（层序遍历）

深度优先遍历

所谓深度优先，顾名思义，就是偏向于纵深，“一头扎到底”的访问方式。

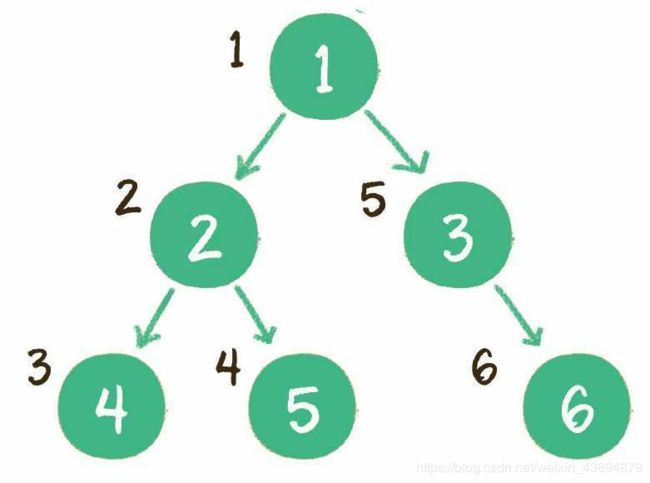
前序遍历
前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。

中序遍历
中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。

后序遍历
后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

三种深度优先遍历的对比

使用递归实现三种深度优先遍历：深度优先遍历代码实现

绝大多数可以用递归解决的问题，其实都可以用另一种数据结构来解决，这种数据结构就是栈。因为递归和栈都有回溯的特性。不过要比递归实现稍微复杂一点。

广度优先遍历

层序遍历，顾名思义，就是二叉树按照从根节点到叶子节点的层次关系，一层一层横向遍历各个节点。

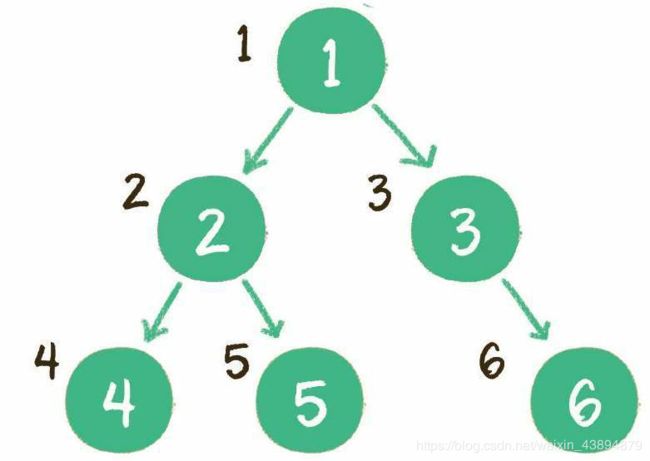
可是，二叉树同一层次的节点之间是没有
直接关联的，如何实现这种层序遍历呢？
这里同样需要借助一个数据结构来辅助工作，这个数据结构就是队列。

详细遍历步骤如下。

1：根节点1进入队列。
2：节点1出队，输出节点1，并得到节点1的左孩子节点2、右孩子节点3。让节点2和节点3入队。
3：节点2出队，输出节点2，并得到节点2的左孩子节点4、右孩子节点5。让节点4和节点5入队。
……
……

使用递归实现广度优先遍历：广度优先遍历代码实现

二叉树和散列表

相对散列表，好像并没有什么优势，那我们为什么还要用二叉查找树呢？

第一，散列表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序。而对于二叉查找树来说，我们只需要中序遍历，就可以在 O(n) 的时间复杂度内，输出有序的数据序列。

第二，散列表扩容耗时很多，而且当遇到散列冲突时，性能不稳定，尽管二叉查找树的性能不稳定，但是在工程中，我们最常用的平衡二叉查找树的性能非常稳定，时间复杂度稳定在 O(logn)。

第三，笼统地来说，尽管散列表的查找等操作的时间复杂度是常量级的，但因为哈希冲突的存在，这个常量不一定比 logn 小，所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时，也不一定就比平衡二叉查找树的效率高。

第四，散列表的构造比二叉查找树要复杂，需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定。

最后，为了避免过多的散列冲突，散列表装载因子不能太大，特别是基于开放寻址法解决冲突的散列表，不然会浪费一定的存储空间。